His Fraudulency
Joe Biteme, properly styled His Fraudulency, continues to infest the White House, we haven’t heard much from the person who should have been declared the victor, and hopium is still being dispensed even as our military appears to have joined the political establishment in knuckling under to the fraud.
One can hope that all is not as it seems.
I’d love to feast on that crow.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices.
Kitco Ask. Last week:
Gold $1808.90
Silver $26.19
Platinum $1105
Palladium $2903
Rhodium $18,500
This week, markets closed as of 3PM MT.
Gold $1812.20
Silver $25.74
Platinum $1105.00
Palladium $2712.00
Rhodium $20,100.00
Not much action this week, other than palladium taking a beating and rhodium staging a partial recovery.
(Update: Real gold can now be had for $125 over paper gold spot prices at places like Kitco. If you arent too fussy about branding you could get even lower (however, you’ll end up selling for less at the other end of the pipe).)
1905 – Quadruple BOOM!!!
(Part XI of a Long Series)
Introduction
Let us start off by recapping our list of mysteries and conservation laws.
- Conservation of mass
- Conservation of momentum
- Conservation of energy
- Conservation of electric charge
- Conservation of angular momentum
The following mysteries were unanswered at the end of 1894.
- Why was the long axis of Mercury’s orbit precessing more than expected, by 43 arcseconds every century? Was it, indeed, a planet even closer to the sun? If so, it’d have been nice to actually see it.
- Why was Michelson unable to measure any difference in speed of light despite the fact we, being on planet Earth that is orbiting the sun, had to be moving through the medium in which it propagates?
- What makes the sun (and other stars) shine (beyond the obvious “they shine because they’re hot” answer). What keeps the sun hot, what energy is it harnessing?
- How did the solar system form? Any answer to this must account for how the planets, only a tiny fraction of the mass of the solar system, ended up with the vast majority of the angular momentum in the system.
What is the electrical “fluid” that moves around when there is an electric current, and that somehow seems imbalanced when we perceive that an object has a charge? Were there both negative and positive fluids, or just one fluid that had a natural neutral level; below it was negative (deficit), above it was positive (excess)?- Why are there so many different kinds of atoms? How did electrical charges relate to chemistry? How is it that 94 thousand coulombs of charge are needed to bust apart certain molecules (though it often had to be delivered at different voltages depending on the molecule)?
- Why were the atomic weights almost always a multiple of hydrogen’s? Why was it never quite a perfect multiple? Why was it sometimes nowhere near to being a multiple?
- Why does the photoelectric effect work the way it does, where it depends on the frequency of the light hitting the object, not the intensity?
- Why does black body radiation have a “hump” in its frequency graph?
I’ve crossed off #5 because J. J. Thomson’s discovery of the electron answered that question.
Because of Max Planck’s work, we had something that might answer #9, depending on how real energy “quanta” were. So I’ll leave that un-crossed-out for now.
And thanks to the discovery of radioactivity we had a hint of a sort of thing that might explain #3. But that’s a lot more tenuous than even Planck’s hypothesis.
With that reminder in place, 1905 saw the publication of four very important papers.
1 – Brownian Motion.
Brownian motion is the jiggling around of bacteria or specks of pollen when looking at them in a drop of water, under a microscope.
This paper used statistical mechanics to come up with a model for how often molecules of water might just happen to “kick” a small object suspended in the water. Statistical mechanics assumes that molecules in a fluid (gas or liquid) will have an average momentum with the particles distributed around that average. Max Planck (and many others) considered it a bit suspect, but today we know it to be the underpinning of thermodynamics. Planck, as we saw in Part X, had found that statistical mechanics could provide a model that would explain the blackbody curve (the Maxwell – Boltzmann distribution). By assuming that atoms could only emit energy in discrete packets, the amount of energy depending on the frequency, he was able to match the curve.
Anyhow, this paper showed that if water consisted of molecules, actual molecules, not just a convenient construct, and statistical mechanics were true, then Browning motion was explained. It had been one of those minor mysteries up until then (one which I didn’t even put in my list, but, let’s face it, I should have).
So now we have a paper showing that Brownian motion is actually hard evidence that atoms and molecules exist, rather than just being a convenient mental “crutch” to understand chemistry. And the position of statistical mechanics is much more solid.
So the last holdouts who didn’t believe atoms were real were finally convinced as this paper made the rounds.
BOOM!!!
2 – Photoelectric Effect
In Part 8, I described how Heinrich Hertz was able to produce, and prove the existence of radio waves. However, he had died in 1894 leaving a bit of a puzzle behind, the photoelectric effect (item 8 on our list of mysteries). Sparks would jump a gap more easily, if ultraviolet light were hitting the gap. Even dim ultraviolet light would have some effect. But lower frequency/longer wavelength light would do absolutely nothing no matter how bright it was.
What turning up the ultraviolet intensity did do, however was cause more electrons to jump the gap, resulting in a bigger spark.
So the frequency had to be high to enable the spark jumping in the first place; if enabled, the intensity was proportional to how big the spark was. If not enabled, no spark, no matter what.
Recall that with a wave, the energy in the wave is in the amplitude, in other words, the intensity of the wave, not its frequency. And Maxwell had pretty much demonstrated to everyone’s satisfaction that light is a wave. Newton had thought it was a particle but between Maxwell and certain earlier investigators who got light to diffract and generate interference patterns (and even measured the frequency of some forms of light), the particle hypothesis looked to be deader than Hitlary Klinton’s conscience.
But this paper begged to differ.
If light came in little pieces, and the energy in those pieces depended on the frequency, then the photoelectric effect made sense. If a piece…call it a photon…had a high enough energy, it could knock an electron loose and it could jump the gap in Hertz’s apparatus. If a photon didn’t have the energy necessary, it wouldn’t. And neither would any number of those low-energy photons, hitting different electrons in the metal.
But even one high energy photon would knock an electron loose; a bunch of them would knock many electrons loose.
So if light consisted of photons and if the energy of a photon depended on the frequency of the light, then the photoelectric effect could be explained.
But this bit about energy depending on frequency should sound familiar (unless you blew Part X off last week).
Yes, this paper invoked E = h ν. Energy depending on frequency, times that h constant.
And so Planck’s crazy idea that just happened to “fit” with black body radiation now also explained the photoelectric effect.
But even more: Planck had concluded that the quantum principle was a limitation on the atoms that emitted the black body radiation. This paper claimed it was a limitation on the light itself.
So now, we can cross off #9. And #8 as well, as a reward for our patience with #9.
But not in 1905. Most physicists rejected this paper at first, because it strongly implied that light was a particle, not a wave. James Clerk Maxwell had pulled together his four equations, after all, and other people before him had succeeded in measuring wavelengths of light. Something that makes no sense if light is particles, not even particles whose name begins with the 17th letter of the alphabet.
Hold on, though, before we go further. Is light a particle or a wave?
The best answer to that, after a lot of tussling in the early 20th century turned out to be: “Yes.” It’s not a wiseacre answer either, it turns out that light is either/or depending on the circumstance, or if you like our host’s formulation, “AND Logic” applies here.
The greatly oversimplified statement would be that light propagates as a wave, as Maxwell showed, but when it interacts with something (generally consuming the photon) it will behave like a particle, as this paper was the first to claim.
OK, that’s counter-intuitive, you say. Why yes, yes it is. It’s a particle sometimes and a wave other times and it will develop it’s sometimes got aspects of both. But physicists a hell of a light brighter than anyone reading these words (and I do read them myself, so I am not excluding myself from this comparison) have wrestled with this for over a century, and as near as they can tell, that’s Just. The. Way. It. Is.
They might pretend to understand it in a deep sense, but the more honest ones will tell you, no they don’t, in fact, they’ll even quote an old saw that if you think you understand it, that’s proof positive you don’t (this was from Richard Feynman). But physicists can describe the behavior to a T, with excruciating precision.
Incidentally, photons themselves have no mass, and no electric charge (even though they carry the electromagnetic force, they aren’t themselves affected by it). So they don’t interact with anything, until they hit something and are absorbed. And “interacting” with something includes being detected by it, like, say, being seen by your eyes. When your eye sees a photon, it’s now gone. Any photon you don’t see, because it misses your eye, is effectively invisible to you and you can’t know it’s there unless it hits something else and affects it in a way that you can see. There will be plenty of other particles that are similar. Many forms of radiation that go right through you, for instance, are harmless–it doesn’t interact with your body. It’s when you stop radiation with your body that you have a problem. (Note, however, that if a charged particle goes through your body, it can cause all kinds of havoc as it passes by, because it affects the molecules in your body, but in turn, you will deflect the particle slightly in the process.)
In 1921 this paper won its author the Nobel Prize. By then the arguments against it had largely been resolved.
BOOM !!!! (even if it was a delayed blast).
3 – The Electrodynamics of Moving Bodies
There was (and is) a conundrum in Maxwell’s equations. If you moved a coil of wire through a stationary magnetic field, a current is induced in the wire. The problem is, if you looked at it from the point of view of the wire, the effect is due to an electrical force. But from the point of view of the magnet, the effect is due to a magnetic force.
Which kind of force it was depended on who was moving and who was stationary.
However, we had known since Galileo that as long as you’re moving without changing speed, the laws of physics look the same whether you’re moving or not. He used the example of a ship moving smoothly through water. You can play dodgeball on that ship (including all that fun velocity, momentum, mass, and force) without having any way of knowing that it’s in motion. If people outside can see the game, they’ll note different velocities (because they will add the velocity of the ship to everything), but still see everything being consistent with Newton’s laws.
All of those things I dragged you through weeks ago work the same if they’re happening in a moving frame of reference…or not. This is now referred to as Galilean relativity: The laws of nature are the same in all inertial reference frames (i.e., ones not accelerating). He put this forward clear back in 1632.
So it shouldn’t matter whether you’re in the frame of reference of the loop of wire (and see the magnet as moving) or in the frame of reference of the magnet (and see the loop as moving).
Oddly enough, the fact that Michelson and Morley had been unable to tell any difference in the speed of light through a vacuum (mystery #2) no matter what direction they measured it in, turned out to be part of the solution for this.
This paper showed that if you posit Galilean relativity and that the speed of light in a vacuum is one of those things that’s always the same no matter what inertial frame you are in, then the conundrum found in Maxwell’s Equations is resolved.
The paper mentioned the Michelson-Morley experiments in passing; later on the author would not even remember he had done so. But their experiment strongly implied the second postulate (the invariance of the speed of light in a vacuum, in any inertial reference frame, even one that’s moving at near light speed as seen by us) is actually true. And indeed we have never, ever seen this fail.
I’ll explain later some of the ramifications of this. Get ready for a bit of a wild ride.
If you measure the speed of light in a vacuum, which is denoted by the symbol c, with perfect accuracy and precision (while riding your invisible pink unicorn, which came bundled with your perfectly accurate and precise lab equipment) you will get precisely 299,792,458 meters per second.
The invariance is so well accepted that now, the meter has been defined in terms of the speed of light. You’ll occasionally read some article claiming that the speed of light is changing. Although scientists are trained to never say never, they’re so confident that c does not change that they define their units by it–if they’re wrong about this it would wreak havoc.
I’ll have more to say about this presently, but first, a minor rant.
To the popular reader in America, the speed of light is often given as 186,000 miles per second. Of course, that’s an attempt to make it more relatable to us Yanks since it’s not in kilometers, but it’s still a fail.
We don’t think in miles per second. We think in miles per hour. (Unless, of course, we’re astrodynamics or rocketry geeks–but those folks have mostly gone metric, outside of some rocket production facilities.)
The speed of light is almost precisely one billion kilometers per hour, or 671 million miles per hour.
That’s not really relatable either, but at least when you read that you know just how unrelatable that is.
Most of us have never even traveled at the speed of sound (since the SST never really took hold). That’s 767 miles per hour at standard temperature and pressure (sea level or 29.92 inches of mercury at 20 C/68 F). Under those conditions, that’s Mach 1. Light moves at Mach 874,837.
It’s going to be a while before we get moving that fast.
The implications of this turn out to be staggering and mind-bending, and I’ve promised to try to walk you through them below.
But because of those implications, this is a BOOM!!! too. And we get to cross Mystery #2 off the list.
Now on to the fourth paper, in some ways the biggest BOOM of all.
4 – Does the Inertia of a Body Depend Upon Its Energy Content?
The third paper seemed to raise paradoxes, so the fourth paper took them on and came up with a surprising result, and I will try to explain that too, below. Here I’ll just state it.
An object, just sitting there, doing nothing, has energy. In fact, because it’s not moving and isn’t kinetic energy, it’s called rest energy.
How much energy? A LOT of energy. A one kilogram object, in fact, contains 89.875 quadrillion joules of energy. That will run a million 100 watt light bulbs for almost 28 1/2 years.
One very big implication of this was that mass and energy were equivalent, meaning that in some cases some mass could become energy.
But that violates the first and third conservation laws I listed up above.
Or rather, it combines them into a new law, the conservation of mass-energy. However, particle physicists just tend to think of matter as a form of energy by preference (it’s more convenient than thinking of energy as a form of matter) so they will still talk about conservation of energy, while never talking about conservation of mass (they see it change far too often…as you will eventually see).
Another consequence is that even a massless particle, like a photon, has momentum. If you recall, though, momentum requires both mass and speed. Well the photon has speed and energy. Energy is equivalent to mass, so it can have momentum. Which is why light sails work in space, albeit not very quickly; the sun’s light can push–ever so slightly–on the sail, which provides a tiny amount of thrust, without the need for rocket propellant. Because the thrust is so small, you have to already be in free fall for it to do any good, but there it is (oh, a super duper powerful laser might succeed in launching a payload, but we probably couldn’t power such a thing without blacking out the entire planet). But not having to put the mass of the propellant onto the space probe means we can launch a bigger actual probe, or launch it at higher speed, or some of each. And you get continuous thrust. It’s surprising how much a continuous small thrust can do over time. This is huge from a space exploration standpoint; if we can get into orbit we can potentially get places cheaply as long as we aren’t in an absolute tearing hurry.
BOOM!!!!
And I do mean “boom” here because that kind of energy can be explosive.
As the Japanese learned on two days in summer, 1945.
Muck with America, and you just might get a physics lesson a lot more painful than any of my posts.
(Talk about physics lessons–right after I wrote that sentence a bolt in my chair broke and I got a few more lessons in physics.
All in 1905
All four of these papers came out in 1905. Some had an immediate impact, others were disregarded, because they were too outlandish.
But today they are all landmark papers, and 1905 is considered one of the biggest years in the history of science, on a par with 1666 when Newton had the key insights that resulted in the theory of universal gravitation and the spectrum and calculus.
Who wrote these papers? I never mentioned their authors, did I.
WRONG. I never mentioned their author.
One man.
This man.

That is a photo from 1904. One year before what is now called the Annus Mirabilis. He was 26 when he wrote those papers.
And in case you still don’t recognize him, here he is in 1947.

Yes, this was Albert Einstein. And he wasn’t done yet!
Oh, and the formula that tells you how much energy there is in a mass (or vice versa)?
E = mc2
The units of E are joules, which are kg m2 / s2. Notice on the right there is mass (kg) and a speed, squared, which is to say m/s, squared. The units match.
The units always must match!
If Albert Einstein had, after all his algebra, come up with some formula where the units didn’t match, he’d have known to start over. Or in other words, this could not have happened (but it’s too funny to pass up).

And yes, c is the speed of light. The one kilogram mass thus has, or rather, is (1kg)(299,792,458 m/s)(299,792,458 m/s) = 89,875,517,873,681,764 joules.
And this is a gigantic hint, as to where the huge amounts of radiation in radioactivity might be coming from.
Roundup
Let’s recap/update those lists.
Conservation of mass- Conservation of momentum
Conservation of energy- Conservation of electric charge
- Conservation of angular momentum
- (ADD:) Conservation of mass-energy
The following mysteries were unanswered at the end of 1894.
- Why was the long axis of Mercury’s orbit precessing more than expected, by 43 arcseconds every century? Was it, indeed, a planet even closer to the sun? If so, it’d have been nice to actually see it.
Why was Michelson unable to measure any difference in speed of light despite the fact we, being on planet Earth that is orbiting the sun, had to be moving through the medium in which it propagates?- What makes the sun (and other stars) shine (beyond the obvious “they shine because they’re hot” answer). What keeps the sun hot, what energy is it harnessing?
- How did the solar system form? Any answer to this must account for how the planets, only a tiny fraction of the mass of the solar system, ended up with the vast majority of the angular momentum in the system.
What is the electrical “fluid” that moves around when there is an electric current, and that somehow seems imbalanced when we perceive that an object has a charge? Were there both negative and positive fluids, or just one fluid that had a natural neutral level; below it was negative (deficit), above it was positive (excess)?- Why are there so many different kinds of atoms? How did electrical charges relate to chemistry? How is it that 94 thousand coulombs of charge are needed to bust apart certain molecules (though it often had to be delivered at different voltages depending on the molecule)?
- Why were the atomic weights almost always a multiple of hydrogen’s? Why was it never quite a perfect multiple? Why was it sometimes nowhere near to being a multiple?
Why does the photoelectric effect work the way it does, where it depends on the frequency of the light hitting the object, not the intensity?Why does black body radiation have a “hump” in its frequency graph?
Almost all of those crossoffs are Einstein’s work.
Even better, two and a half of the rest of the items will get crossed off in the future, either by Einstein, or by people using what he did in 1905.
Boom!!! Boom!!! Boom!!! and KABOOM!!!!

Special Relativity
The third and fourth of Einstein’s 1905 papers were on what we today call “Special Relativity” and some of its implications. It’s “special” relativity, because it applies only to inertial reference frames, a “General” theory of relativity would apply even to accelerating reference frames.
I’m going to be honest with you, this won’t be easy to explain, and it won’t be easy to understand, either. So let us gird our loins, and jump in.
The two postulates are 1) that the laws of physics are the same in any inertial reference frame, and 2) that the speed of light in a vacuum, c, is the same in any inertial reference frame.
The first was and is utterly uncontroversial. Galileo had used the example of a smoothly moving ship (as in sea vessel) to explain it clear back in 1632. (The only thing that had changed by 1905 was that people would used moving trains to visualize the principle. Gotta keep up with progress. Nowadays we use rocket ships or airplanes. But we’ll stick to vintage 1905 imagery for now.)
The second postulate doesn’t sound too crazy, either, right? If you’re standing on a train, moving at, say, 60 percent of the speed of light and aim a laser pointer directly ahead, and light it off, you expect it to look to you like it’s moving away at the speed of light. And the same if you fire it sideways, or backwards. Just as if you were firing a gun, or throwing a baseball. (Nor does it matter if you’re doing something distinctly less American.) You shouldn’t be able to tell the train is moving, or in which direction, just by the way the light, or bullet, or baseball (or, egad, soccer ball) behaves.
And likewise, if you’re instead standing on the railway station platform. Things should look the same there, too. You can’t tell which frame of reference is moving, because there is no “God’s Eye point of view” fixed, absolute reference frame. Any such frame can be treated as if it were fixed and the rest of the universe were moving.
Yes, that seems reasonable. But this will not: If you’re standing on the train and point the laser pointer straight ahead, and turn it on, not only will you measure its speed as c, but so will someone standing on the railroad platform!!! Now, you would expect the guy on the railroad platform to measure 0.6c + 1.0c = 1.6c for the speed of the light beam coming off the laser pointer, but he does not. He measures it as c. You cannot just add the velocities together, as you do for baseballs and bullets and trains. When I said “the speed of light in a vacuum, c, is the same in any inertial reference frame,” I meant it, thoroughly. It applies even to a beam of light starting in some other reference frame!
How can this be?
Velocity, remember, is distance over time. If the velocity stays the same no matter what, perhaps the time and distance don’t.
Time Dilation
Well, let’s think about this somewhat mathematically. Light travels a bit less than a foot in a billionth of a second (a nanosecond). So I’m going to actually define a new unit of length, a bit less than a foot, the distance light travels in a billionth of a second. I am going to call it a pod (from the Greek for “foot,” as in tripod and bipod, to say nothing of tetrapods (amphibians, reptiles, birds and mammals)). Expressed in pods, then, c is 1 pod per nanosecond ( 1 pod/ns ).
So returning to our 0.6c train, in the time it takes light to move ten pods’ distance (a hundred-millionth of a second), the train moves 6 pods’ distance.
Imagine the inside of the train car is 8 pods high, and call that distance L. Your friend is in the train, and he sets a laser pointer on the floor, pointing straight up. On the ceiling is a mirror, and the pointer also has a detector in it, waiting for the reflected beam. He sets the laser pointer to fire a very short burst instead of continuous beam.
He fires it off, the pulse goes straight up, bounces off the mirror, and comes straight back down. Total trip, 16 pods, total time 16 nanoseconds. Like in the picture below:
But what do you, standing on the railway platform, see?
You see the pulse of light traveling from the floor of the train, up at a slant to hit the mirror on the ceiling (because the train is moving, remember), then back down at the same slant to hit the detector.
Rather than turn this into a story problem and ask you to figure out how long D and 1/2 v delta t prime is, I’ll give it to you. D is 10 pods long. The train moves 60 percent as fast, so going from A to B it moves 6 pods. The light beam travels a total of 20 pods (10 each way). So our lengths are 8, 6 and 10 pods (and our times are 8, 6 and 10 nanoseconds). This is consistent with Pythagoras:
c2 = a2 + b2
102 = 82 + 62
You measure the pulse’s speed as c, and measure the time it took to be 20 nanoseconds.
The same trip took 16 nanoseconds as far as the man on the train is concerned, and 20 nanoseconds as far as you are concerned.
This is not an illusion. If you could see a clock running on that train as it went past, it would show as running 20 percent slow. Time would actually be slower on the train, as seen from outside the train.
If this seems totally against your intuition–that time can literally crawl just because of how fast you’re moving, you’re not alone. You never see that in real life.
But in real life you don’t move close to light speed, either!
This is time dilation. It’s absolutely real, and has been confirmed again and again and again in experiments for the last 116 years.
And you thought time zones were bad.
Given something moving past at some speed, how much is the time dilation? Gee, I think it’s time for some algebra. I’m going to call the time running on the train tt, the time on the platform tp, and the speed of the train vp (v as seen from the platform. vt, the speed of the train seen from the train, is, of course, zero.) I’m doing this instead of what’s in the diagrams because I find it hard to keep track of what the tick mark means (and I think these diagrams are using it for the other side of things than my physics textbook did, to boot).
OK, so the time measured on the train is:
tt = 2L/c.
Pretty simple.
For you on the platform, you need 2D, and you can get there with a right triangle and Pythagoras, solving for D (which is ctp/2)
[ctp/2]2 = L2 + [tpvp/2]2
So let’s do some cleanup here. First multiply everything by 4, it will get the two-squareds out of the denominators.
[ctp]2 = 4L2 + [tpvp]2
Then divide by c2 and just write out all the squareds in full:
tp2 = 4L2/c2 + [tpvp/c]2
tp2 = 4L2/c2 + tp2vp2/c2
Now bring the tp2vp2/c2 on the right over to the left.
tp2 – tp2vp2/c2 = 4L2/c2
Factor out the tp2:
tp2[ 1 – vp2/c2] = 4L2/c2
Divide both sides by what’s in the square brackets.
tp2 = 4L2/c2 ( 1/[ 1 – vp2/c2] )
Now take the square root of both sides.
tp = 2L/c ( 1/sqrt[ 1 – vp2/c2] )
But, going way back, the guy on the train measured the total time as tt = 2L/c, so:
tp = tt ( 1/sqrt[ 1 – vp2/c2] )
That whole thing inside the parentheses shows up again and again, so it’s often written as gamma (γ).
tp = γtt
Let’s check this against our original specific example, of the train moving at 60 percent of c.
vp/c is 0.6. Square this, and get 0.36. Subtract from one, get 0.64. Take the square root, get 0.8. Divide that into one, get 1.25–that’s γ. And indeed the time on the platform, 20 ns, is 1.25 times the time measured on the train, 16 ns. Cool!
Let’s examine γ some more:
γ = 1/sqrt[ 1 – vp2/c2]
When v is very, very low, like, say walking speed which is about one billionth of c, then v/c is a small, small fraction, and if you square it, it gets even smaller, it’s now a quintillionth. Subtract from one, and you still get, basically, one, as close as you can measure it, just a bit under. Take the square root and you get even closer to 1, and when you divide that into one, you get a number just a teensy bit over one. So both times are so close to being the same, you can’t tell the difference. And this is what you see in everyday life.
Now set vp to 86.6 percent of the speed of light. Dividing by C of course you get .866; square it and you get .75, subtract from one and get .25, take the square root of that, get 1/2, divide into 1 to get 2. Two hours, two years, pass on the platform for every hour or year on the train.
Note that you have to get to over 86 percent of the speed of light just to make γ equal to 2. After that, though, it takes off. At 99 percent of light speed, γ is 7. At 99.9 percent of light speed, γ is 22.3. Which means the entire Barack Obola administration, which was about 22.3 years long [wasn’t it?], could have gone by in one year.
The number explodes the closer you get to light speed. When actually at light speed, the part inside the square root sign becomes zero, and you are dividing 1 by zero. Technically you’re not supposed to say “that’s infinity”, but that’s basically what it is.
γ is always one or more. Sometimes a lot more.
OK, if you’ve thought about this a bit, you’ve probably come up with an objection to this.
If I see the train traveling at 0.6c and its clocks are running slow, how about what the people on the train see when they look at the big clock on the station tower, as they move past it? From their point of view, the station is moving at 0.6c (albeit backwards); shouldn’t they see its clock run slow, too?
Yes, they do.
Doesn’t that seem contradictory, though? How can you have two clocks, and each one is slower than the other?
I don’t have a good intuitive explanation of this one, and the one I found on wikipedia is kind of weak, too (they drew an analogy to two people far apart both looking small to each other). The fancy explanation is, you can’t really get into a contradiction until you bring the two clocks close to each other, stationary with respect to each other, and check total elapsed time. But doing that means you have to decelerate one (or both) of the clocks, and once you’ve done that you’re not dealing with inertial rest frames any more. The frame that accelerated is now a different case from the one that didn’t, they’re not symmetric any more and one clock can indeed mark off less total time than the other without it being a contradiction.
I’m sure you’ve heard about the “twins paradox” too. One twin gets on a starship, takes a long journey at close to the speed of light, comes back, and he ends up being younger than the other twin, who stayed behind. The same objection seemingly applies. From the point of view of the traveling twin, the guy who stayed behind traveled away from him and came back, why isn’t he the younger one, or better yet, why are they not the same age at the end?
The reason why is because the traveling twin accelerated, decelerated at his destination, accelerated to come back, and decelerated to arrive back here on Earth. He was not in an inertial frame, but the stay-behind twin was.
That sounds pretty arbitrary and lazy, but the more detailed answer involves going back to our train and railway platform, and demonstrating that two events in two different locations that seem simultaneous to someone at the platform will not seem simultaneous to someone on the train…and vice versa. I’ll talk about that in a moment, but first there’s something else to get out of the way.
Length Contraction
Imagine a passenger on that train…the one moving at 0.6c. He’s going to a destination six trillion pods away. Light covers a billion pods a second, so light would cover this distance in six thousand seconds (less than two hours). The train, though is moving at .6c and conveniently will take exactly ten thousand seconds to make the trip. But the clock on the train is running slower, it’s running at 80 percent of the speed of the clock at the station. The people on the train will perceive that 8000 seconds have gone by when they reach their destination. But the train measures the rest of the world’s velocity as .6c backwards. Multiplying the time by the velocity, they will think the trip was only 4.8 trillion pods (4/5ths) as far.
This is length contraction.
This too is symmetrical. The people on the train see the world shortened in the direction of travel. But the people on the ground see the train shortened in the direction of travel, too. Remember, from the standpoint of the train, the clock on the platform is running slowly as the train goes by, so it must take less time for those people on the platform to see the train go by, than it would otherwise. So they see the train 20 percent shorter than it would be, were it standing right next to the platform at rest.
In fact if lt is the length of the train, as seen on the train, and lp is the length of the train as seen from the platform:
lp = lt/γ
This time you divide by gamma. And again, this effect is totally immeasurable and imperceptible at day-to-day speeds, but it’s as real as Joe’s pedophilia at close to light speed. Again, it has been measured, time and time again.
Simultaneity
Now it’s kind of hard to get a handle on “simultaneous.” How can you tell that two events happening fairly far away (but in different directions) are simultaneous? If there is a flash of light to the north, and another to the south, how can you decide they’re simultaneous, when you know it took some amount of time for the light from the two events to reach you?
Well, the simple case is if you’re halfway between the two events. The light from both should arrive at the same time if they’re simultaneous, because in both cases they had to travel the same distance. Similarly, if you know the distances to the events, you can simply correct for light speed delay even if they’re not equidistant from you, figure out when the events happened by subtracting the delay from when you saw it happen, and compare.
OK, let’s go back to the railway station.
You set up a pair of sensors. When the train reaches the sensor, it will flash green. When it passes the sensor (i.e., the sensor sees that there is no train right there any more) it will flash red.
Now you set the sensors as far apart as the length of the train, on the edge of the platform (after figuring in its contraction).
You stand precisely in between the sensors.
When the train reaches the first sensor, it flashes green. When it reaches the second sensor, that sensor flashes green, but the train is just finishing passing the first sensor, so it flashes red at the same time. You see the red flash and the green flash simultaneously, and you know you’re standing exactly midway between them, so you conclude that you got the two sensors at the right distance because the train started passing one at the same instant it finished passing the other.
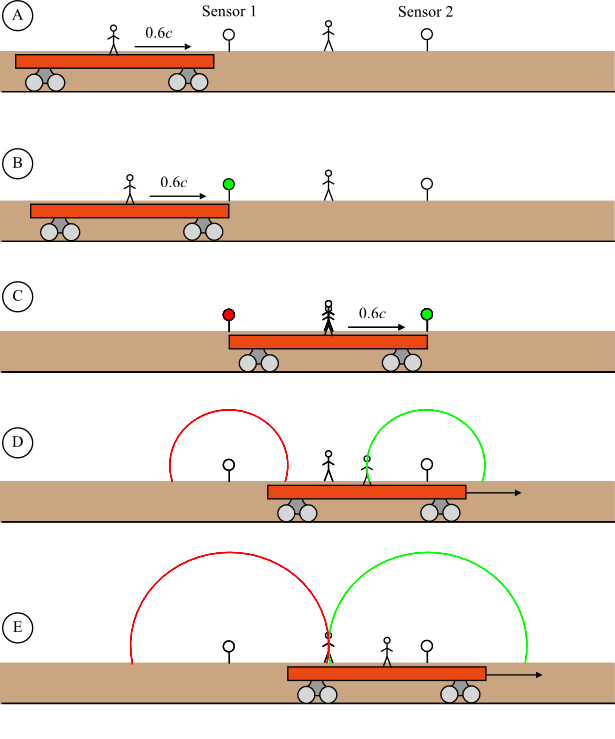
B. Train reaches the first sensor, it lights green
C. Train now reaches the second sensor, which lights green, and is done passing the first sensor, which lights red. There is a clock at each sensor that reads midnight at this moment.
D. The man on the train sees the green flash from sensor 2, but NOT the red flash from sensor 1 even though he was midway between them when they flashed. He also sees that the clock at sensor 2 shows it is midnight.
E. The man on the platform sees both sensor flashes at the same time, and he says, ah, ha! I’m halfway in between them so I know they both fired simultaneously. They both show midnight. Meanwhile the man on the train still hasn’t seen sensor 1 flash. When he finally does, he’ll see it says midnight and he’ll conclude that sensor 2 (which from his point of view is chasing sensor 1) has a clock that is running fast compared to Sensor 1.
What about someone standing in the middle of the train? He is moving toward the second beacon as it flashes green, and away from the first beacon as it flashes red. He will therefore see the green flash before the red flash. At the time you see them both flash, he is already down the track, and therefore must have seen the green flash already! Since he knows he was midway between the beacons (from his viewpoint one was at the front of the train, the other at the back), and he knows the speed of light is a constant, he concludes that the two flashes were not simultaneous, the green flash from the front of the train came first.
This is actually consistent with the length contraction of the station that he sees. He sees that the sensors are too close together because of the length contraction, thus the front of the train reached the second sensor before the back of the train reached the (too close) first sensor. Thus the first sensor fires its red flash after the second sensor fires its green flash. And that is precisely what he saw happen.
If you are thinking that this is an artifact of the fact that the train is moving and the platform is stationary, think again. From the standpoint of the train, the train is stationary and the platform is moving. From the standpoint of a third party, they might both be moving while that third party is at rest.
None of these reference frames is any better or “truer” than the others. That’s what the Galilean equivalence means. You can’t even tell which one is moving by measuring how fast light moves in the stationary aether…as Michelson and Morley demonstrated (to their puzzlement at the time)…because there is no stationary aether.
Imagine that there is a clock right next to each sensor, and that the train passed them at midnight, precisely. The guy on the train will see the second clock the same time he sees the green flash, and it will say midnight. Later on he will see the red flash from the first sensor, and see that the clock there reads midnight. From his standpoint the clock that passed him first (going backwards) at sensor one, is lagging behind the clock that is “chasing” it (clock and sensor #2). And the formula for just how far off they are is:
t2 – t1 = L v /c2
Here L is the length of the train, as seen on the train. In other words, the length of the train when you don’t see it as moving, because if you see it moving, its length will contract. The answer is how far the second (chasing) clock is ahead of the first (leading) clock in the train’s reference frame, when the two clocks are synchronized in their own (platform) reference frame.
If the train is 60 pods long, those two clocks will seem to be off by: 60 x 0.6pod/ns divided by 1 pod2/nsec2 = 36 nanoseconds, which given how fast things are moving and how short our time scale is, is very significant. The train requires 100 ns to move its length, and the apparent discrepancy in the clocks is over a third that much.
The Twins Paradox
Now we can go back to the “twins paradox.” Let’s say the ship is going to Sirius, which close to 8 light years away (we’ll ignore the difference for purposes of illustration). A light year is the distance light travels in a year, so light would take eight years to make the trip. From d = vt, we can write a light year as ct with t in years (1), and c in meters per year instead of per second. And let’s figure the ship is going to travel at .8c. The ship will therefore take ten years to get there, as seen from earth. It will then immediately turn around and come back at the same speed. Total time, as seen from earth, 20 years.
Billy is going on the expedition. Bob is staying home.
Bob analyzes the trip. He sees the ship traveling 8 light years at .8c and concludes the one way trip will take ten years. Two ways, 20 years.
Let’s look at Billy’s perspective. Calculating γ at 1 2/3s, he can divide by that (since he’s going to be the one on the train, by the math) and see that the distance to Sirius will contract by 40 percent (he will multiply it by .6). So once he’s on that ship, traveling at .8c, Sirius will be 8 x .6 = 4.8 light years, and traveling at .8c, it will take him six years, one way, 12 years round trip.
From Billy’s point of view, however, it’s Bob that’s doing the traveling, so he should be younger than Billy when they meet again. In fact, while Billy ages 6 years, Bob should be aging 6 x .6 = 3.6 years, or in total, Billy ages 12 years, Bob ages 7.2 years. Not 20! So Billy is scratching his head, wondering how that “twenty years” of aging that Bob will do, possibly can be.
It’s resolved this way. Imagine a clock on earth, and a clock at Sirius, that were synchronized with each other. A person midway between them, at rest with respect to both of them, sees them both reading four years ago (he is four light years from each clock, so their signals are delayed by four years when they reach him).
While Billy is traveling to Sirius, it’s going to look like two clocks moving past him at .8c, separated by 8 light years. It will look like the one at Sirius is chasing the one at earth. Go back to our formula:
t2 – t1 = L v /c2
L is 8 light years, v is equal to 0.8 c, so the Sirius clock looks to Billy (after correcting for all light-speed delay) as if it were 6.4 years ahead of the clock on Earth. (You have to convert everything back to meters and seconds and use 299,792,458 meters/second for that to work out. I just did it, that’s the right answer.)
So Billy arrives at Sirius, and stops. He’s now in the frame of reference of the Sirius clock, which, remember, was, while he was moving, 6.4 years fast. The clock did not just run backwards, so it still reads what it read before. But that means the clock back on earth must have advanced 6.4 years while Billy was slowing down to a stop, because in this reference frame, the two clocks are synchronized. So Billy thought Bob had aged 3.6 years during the trip; now he has to add 6.4 years to that to get…10 years. So Bob ages ten years during half of the trip.
It might also help to have the two twins send each other messages once a year (as they perceive it). Each twin can then monitor the aging of the other by simply counting signals. They don’t even need to correct for light speed delay, because they will receive all of the signals sent by the time they are re-united at the end of the round trip; some will be later than others but all will get there before the end of the trip. As it turns out, when they are moving further apart, each will get a signal from the other once every three years. When they are heading towards each other, the signals arrive every four months (a third of a year).
Looking at it from Traveler Billy’s point of view, during the six years he spends traveling to Sirius, he gets two signals. When he turns around and heads back to earth, he starts getting three signals a year for six years, total eighteen, grand total 20. The last signal from Bob reaches Billy in earth orbit just as the journey ends. Bob aged twenty years.
From Stay at Home Bob’s point of view, while Billy is travelling out for ten years, he gets three signals, the last arriving at year nine. But then he continues to get signals after ten years, from Billy as he was traveling outwards, because the last signal was sent from Sirius, eight light years away, ten years after the trip started. So Bob gets six signals over the course of eighteen years. Then the signals from Bob as he’s coming back arrive, 3 per year, for two years, for a total of six more signals, including the last one from earth orbit that arrives just as Bob arrives. total, twelve signals; Bob aged 12 years.
There are aspects of this I could not cover, including the Doppler shift, which is how one gets the 3 per year, one every three year numbers I just used.
I also didn’t have time to explain how E = mc2 comes from all of this (Einstein’s fourth paper, the big kaboom!!! both literally and figuratively).
But I am running out of time and I have to produce the diagram for simultaneity still (no good one to be had online). But it’s now done and it’s 12:26. Just need to fix the precious metal prices!
Obligatory PSAs and Reminders
China is Lower than Whale Shit
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!
