Joining The Herd Of Lemmings

I’ve had cause to consider a few things. Maybe we’re going about it the wrong way, and we need to ditch Trump

Yeah, NO

Trump all the way! Why? Because being hated by the people who hate him is a sign of impeccable character, that’s why.

The haters can go fuck themselves with rusty twelve gauge bore brushes. I’d prefer ten gauge but that’s kind of scarce, so…I’m willing to compromise.

The RINO’s Dilemma

The RINOs who who have burrowed in and taken over most GOP organizations, from the state down to local organizations, have quite a dilemma on their hands, and most of them have their heads too far up their asses to realize it.

OK, I’m not talking about the liberal in a Republican area, who knows they’re in the wrong party, but is there because it’s the only game in their town; they hope to capture a nomination someday, at which point they’re guaranteed to be elected…otherwise, they never will be. These people are a hazard in any heavily conservative area.

No, I’m talking about the guys who are a little bit conservative and want to do some good by going into politics, and they’re in a closely matched area, closely enough that they can join the party they are most aligned with and still have a chance. They think the Democrats…particularly the ones who end up running for office…are nuts.

They don’t think much better of the Deplorable types, either. A bunch of bumpkins whose hearts are in the right place, mostly…OK a bit extreme. But they think Deplorables can’t understand that first you have to get elected, then work within the system to change things…a slow process. They genuinely want many of the things Deplorables want…just not as much. The government is spending too much. Or they need to spend money on highways instead of welfare for illegal immigrants. But they want to work within the system to get these things done.

Or maybe they think things are pretty close to ideal right now, and they want to nail it in place.

The problem is, that means they don’t stand for anything in particular. And it shows. They’re about as unappetizing to the electorate as a puddle of dog vomit. The folks in the middle, who they think they are appealing to because they themselves are not extreme, would honestly prefer a clear-spoken radical to someone who qualifies everything they say to the point where they sound like they don’t believe anything at all.

The problem these “Mild RINOs” have, is they just can’t see that. And the reason they just can’t see that, is their entire sense of self-worth is tied up in not seeing that. In their minds, they’ve worked tirelessly for their party, to keep those crazy Democrats out…only to have to constantly fight with a small number of crazy Republicans–who are only liabilities if they end up as candidates. They’ve fought the good fight, and if they can just find the right candidate, someone with some charisma, they might stop the crazies…without being too beholden to the OTHER crazies. In the meantime it’s not working. What’s a responsible guy in politics to do?

They simply cannot understand that the Republicans can’t succeed as the party of nothing in particular. Not really in the past, and certainly not today when people are starting to realize that no matter what they do in the voting booth, the country is still about to fly off a precipice. If they did see it, they’d suddenly have two choices: Go away and let the GOP succeed, or stay and fight. But “go away” isn’t really an option, because what’s the point of having a party now owned by the crazies, win?

Well, they have a dilemma…and WE, therefore have a problem. And we would have that problem even IF they realized that they had a problem…that they were the problem.

No one ever thinks they are the bad guy. Even Epstein probably thought he was the good guy. Right up to the moment where he didn’t kill himself.

So if you ever wonder why these unappetizing dufuses cling on even when their fingernails are being left behind…that’s why. They don’t understand no one wants them, and can’t imagine that no one should want them. And oftentimes their greatest pride is in all the hard work they’ve done for the party. They’re not going to give that up; it’d be psychological suicide.

If you’ve worked with these people, there’s a good chance you like them and consider some of them your friends. But even if so…we’re going to have to give them a good, hard shove. Because America is more important than those milquetoasts’ egos.

Justice Must Be Done

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines,  here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.

(Hmm a few extras seem to have crept in.)

Spot (i.e., paper) Prices

Last week:

Gold $1,955.30
Silver $24.96
Platinum $982.00
Palladium $1,304.00
Rhodium $5,450.00

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $1,961.90
Silver $24.66
Platinum $972.00
Palladium $1,322.00
Rhodium $4,750.00

Gold creeping upward. Other things decidedly mixed, with little movement, prercentage wise. Except of course rhodium which continues its collapse.

Comparing Cartesian And Polar Coordinates

Last week I introduced polar (circular grid) coordinates as an alternative to (and equivalent of) Cartesian (square grid) coordinates.

I also stated that because they’re equivalent either one could be used at any time, so you could pick whichever one was most convenient at the time.

What did I mean by that? Well, hold that thought.

I was talking about x, y pairs last week, but I could just as easily have been talking about complex numbers. Remember they can be represented on a plane that looks a lot like the Cartesian plane, with the real part taking the place of x, and the imaginary part standing in for y. So you can convert complex numbers to polar coordinates, too…but there’s a hitch. The resulting r and θ do not map nicely to real and imaginary, the pair as an inseparable whole is part imaginary and part real. You just have to remember that the thing represents a complex number, and if you want to split it up, you have to convert to Cartesian.

In polar coordinates, r is often called the “absolute value” of the complex number (or you can think of it as the magnitude or length), while θ can be called the “argument.”

Actually…this is not standard notation, but for clarity I am going to surround polar-style complex numbers with angle brackets: < and >

OK, now let’s consider the complex number plane, in both Cartesian and polar forms. And let’s look at some examples.

We’re going to represent a couple of complex numbers in both ways and do two different things to them in order to see which system is more convenient for each of those things.

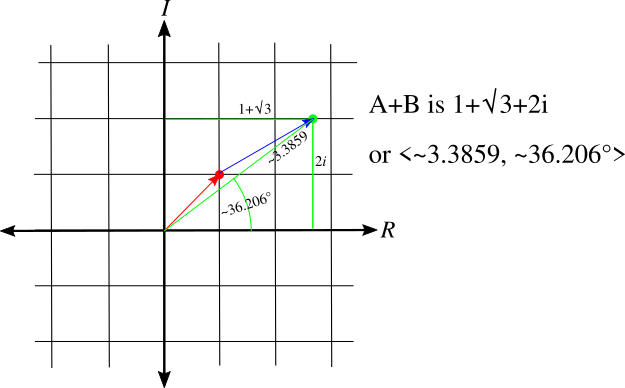
The first example number we will call A, and in Cartesian form, it is 1+i. Converting to polar coordinates, it’s <√2, 45°> or <√2, π/4> depending on whether you’re thinking in degrees or radians.

The second pair is B and in Cartesian coordinates, it is √3 + i. Converting to polar coordinates, it’s <2, 30°> or <2, π/6>, depending.

[Angles like 30°, 45° and 60° degrees are the “easy” angles in trigonometry because their sines and cosines are well known and fairly simple; the sine of 30° is 1/2, the cosine is √3/2. For 45° both the sine and cosine are √2/2. For 60°, swap the sine and cosine of 30 degrees. Other easy angles are 0 and 90°, plus of course any corresponding angles in the other quadrants of the plane, e.g. 120° is simply the mirror image of 60° so its sine and cosine are going to be the same except for the cosine changing sign to -1/2. People who have been doing trigonometry for very long simply know these angles, and their matches in other quadrants, off the tops of their heads. So (returning to our two example complex numbers), A is at 45° but its length is clearly not 1 since both the x and y (real and imaginary) values are 1. We can get the length from Pythagoras, though, x² = 1 and y² = 1, so the hypotenuse (the length of A) squared is 1+1=2, so the length of A is √2. For B, I simply doubled the well-known sine and cosine of 30°, so I’ve got a 30° angle and a length of 2.]

OK, let’s add A + B. That’s easy to do in Cartesian coordinates, it will be (1+√3) + (1+1)i. (If you remember vector addition from the physics series, this works exactly the same; you can even treat the two numbers as if they were vectors and do a tail-to-head visual addition.) So what do we get in polar coordinates? Well, it’s not obvious how to add things in polar coordinates…but let’s convert the sum into polar coordinates just to see if some sort of pattern suggests itself. Doing so, we find that 1+√3 + 2i converts to <3.3859, 36.206°>…approximately.

Yuck.

There’s no obvious way to get from <√2, 45°> + <2, 30°> to get <~3.3859, ~36.206°>. Not even if you write 1.414… for √2. You can add 1.414… and 2 and get 3.414…but that’s different from 3.3859. It’s close but not close enough. In fact if you actually did do a tail-to-head vector addition diagram, you saw why. The two “vectors” are in almost, not quite the same direction, so the sums of their lengths is not that much greater than the length of their sum. But it’s not the same. And of course the angle 36.206° has no obvious derivation from 45° and 30°. It’s not halfway in between or anything like that.

So it seems that, if you want to add x, y pairs, or complex numbers in Cartesian form…you’d better leave them that way. Adding those is easy. Adding r, θ pairs looks a lot more complicated. So, for addition, the Cartesian form is most convenient.

How about multiplication? Multiplication is defined for complex numbers (but defining it for vectors gets a bit dicey). Okay, so let’s do the multiplication.

(1 + i) x (√3 + i)

Remember for complex numbers, you use “FOIL” (first, outside, inside, last), a generalization of the rule that you multiply everything in the first vector, complex number, or whatever, by everything in the second, then combine like terms.

1 x √3 = √3 (first)
1 x i = i (outside)
i x √3 = √3i (inside)
i x i = -1 (last)

Gathering like terms together, we have (I’ll put parentheses around the real and imaginary parts for clarity):

(√3 – 1) + (√3+1)i.

This seems kind of almost-symmetrical, but it’s a mess, actually.

OK. It’s not obvious here how we’d use polar coordinates to multiply, so let’s just convert the answer and see what pops out.

The first component, r, is going to be the square root of the sum of the squares of the real and imaginary parts. That’s basically Pythagoras, r² = (real part)² + (imaginary part without the i)²

Squaring both pieces (again using FOIL) we get:

(3 – 2√3 + 1) [first part, squared] + (3 + 2√3 + 1) [second part, squared]

(Note that we don’t include the i in the squaring because we are trying to assess the sizes of the sides of the triangle, and those are all real numbers.)

And lo and behold the 2√3’s cancel and we’re left with r² = 8 = 4×2, so r = 2√2. Which is sort-of tidy. And the angle turns out to be (I won’t show the work, but I pushed it into a calculator even though I know the answer already because…well, you’ll see): 75°.

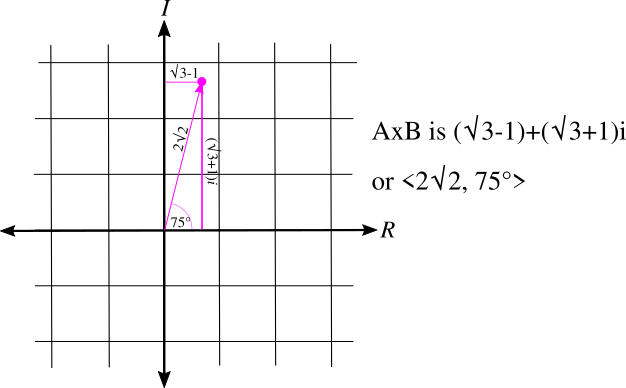
Exactly 75°.

OK now set <2√2, 75°> next to the polar version of the two pairs we were multiplying and see if anything strikes you as a pattern.

<√2, 45°> x <2, 30°> = <2√2, 75°>

Now if this were a video, I’d either wait a while or ask you to pause it and think about it.

But really…look. The rs multiplied, √2 x 2 = 2√2…and the angles added.

Geez, that is a lot less tedious than FOIL. In fact it’s almost as easy as adding the numbers is in Cartesian mode!

As it turns out, multiplying any complex number, by some other complex number, gives you another complex number with magnitude equal to the product of the two numbers, and angle the sum of the two angles. Or you can think of it as rotating the first number by the angle in the second, and then multiplying the two magnitudes.

So which mode is more convenient for multiplication? You’ve got it: the polar mode.

And as an extra bonus, we have a way to rotate a complex number. (And similar ways to rotate vectors.) Multiply it by another complex number with the desired angle. And unless we want the magnitude to change, make sure the “rotator” complex number has magnitude, r, equal to 1.

A “rotator” complex number like that will have, as its real component, the cosine of the rotation angle, and as its imaginary component, the sine of the rotation angle. Or in other words, <1, θ> a/k/a cosθ + isinθ will, by multiplication, rotate another complex number on the complex number plane by the angle θ.

This may seem like nothing more than a parlor trick for geeks, but it turns out to be very, very important in the technical realm, particularly with electrical and electronic engineering. Whatever it is you’re reading this on, ultimately depends on this fact.

OK that’s enough for now!

Fuck Joe B*d*n

Due to complaints about foul language, I’ve censored the most objectionable word in the title of this section.

B*d*n, you don’t even get ONE scoop of ice cream today.

(Please post this somewhere permanent, as it will continue to be true; the SOB will never deserve a scoop.)

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!