What is it that feeds our battle, yet starves our victory?
January 6 Tapes?
Where are the tapes? Anyone, Anyone? Bueller? Johnson??
Paging Speaker Johnson…this is your conscience calling you out on broken promises.
Evading Reality
Many things the Left believes are simply not true. Right now the focus is on the size and scope of our government, and the many many billions of dollars the government has been spending on no-one-knew-what. None of that money is going to a key role of government. Which, after all, has the sole purpose of protecting rights.
And if you, Leftist Lurker, want to dismiss this as dead white cis-male logic…well, you can call it what you want, but then please just go fuck off. No one here buys that bullshit–logic is logic and facts are facts regardless of skin color–and if you gave it a moment’s rational thought, you wouldn’t either. Of course your worthless education never included being able to actually reason–or detect problems with false reasoning–so I don’t imagine you’ll actually wake up as opposed to being woke.
As Ayn Rand would sometimes point out: Yes, you are free to evade reality. What you cannot do is evade the consequences of evading reality. Or to put it concretely: You can ignore the Mack truck bearing down on you as you play in the middle of the street, you won’t be able to ignore the consequences of ignoring the Mack truck.
And Ayn Rand also pointed out that existence (i.e., the sum total of everything that exists) precedes consciousness–our consciousnesses are a part of existence, not outside of it–therefore reality cannot be a “social construct” as so many of you fucked-up-in-the-head people seem to think.
So much for Leftist douchebag lurkers. For the rest of you, the regular readers and those lurkers who understand such things, well here we go for another week of WINNING against the Deep State.
I confess that the novelty has not worn off.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Yes, we won this time around. Not only did we win, we got to KEEP that win instead of having it stolen from us.
But no one should imagine that that’s the end of electoral fraud. Much work needs to be done to ensure it doesn’t just happen again next time around. And incidentally to rescue those states currently in the grips of self-perpetuating fraud, where the people who stole the last election, make sure it’s easier to steal the next one.
This issue, though it’s not front-and-center right now, is not going away, and if we ignore it, we’ll pay the price. See the article above about the consequences of evading reality.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices.
Kitco Ask. Last week:
Gold $2,985.50
Silver $33.87
Platinum $1004.00
Palladium $988.00
Rhodium $5,700.00
FRNSI* 143.424-
Gold:Silver 88.146-
This week, markets closed as of 3PM MT.
Gold $3,024.40
Silver $33.10
Platinum $988.00
Palladium $984.00
Rhodium $6,100.00
FRNSI* 145.305+
Gold:Silver 91.372-
Gold was actually up in the 3040s Wednesday and Thursday but dropped on Friday, (which has been a common pattern for years). Platinum went nowhere. Silver is actually down. My understanding is that gold’s rise has been driven by central bank purchases. Since they don’t bother with silver, that explains why silver is basically tango uniform. The gold:silver ratio has been above 100 before, and I would be surprised if it doesn’t get there again soon.
*The SteveInCO Federal Reserve Note Suckage Index (FRNSI) is a measure of how much the dollar has inflated. It’s the ratio of the current price of gold, to the number of dollars an ounce of fine gold made up when the dollar was defined as 25.8 grains of 0.900 gold. That worked out to an ounce being $20.67+71/387 of a cent. (Note gold wasn’t worth this much back then, thus much gold was $20.67 71/387ths. It’s a subtle distinction. One ounce of gold wasn’t worth $20.67 back then, it was $20.67.) Once this ratio is computed, 1 is subtracted from it so that the number is zero when the dollar is at its proper value, indicating zero suckage.
The Math Behind Radiometric Dating
This is going to be a bit brutal for those who are math phobic. For the rest it will reward careful attention.
Radiometric dating involves, at the very least, measuring the quantities of parent isotopes and daughter isotopes. In some situations it gets more complicated than that, and to be honest those situations are actually the usual ones.
Introducing Uranium-Lead Dating
So let’s take an actual case as an example, a method called uranium-lead dating, because the parent isotope is uranium, and the daughter isotope is lead. Actually there are two sets of parent-daughter isotopes in this case: uranium-238 with daughter isotope lead-206, and uranium-235 to lead-207. (Check: The differences between the mass numbers must be a multiple of 4, because a change of 4 is the effect alpha decay will have. And yes it looks like I got the right numbers. I saw a video recently that swapped the lead isotope numbers; an easy mistake to make.) This makes it a favorite because you can do two datings with one sample.
For simplicity we will start by considering only the uranium-238 to lead-206 pairing. Most dating methods use an isotope that decays directly into the daughter product. U-238 does not do this. It decays into thorium-234 by alpha decay, then there are a chain of thirteen more decays (there are alternate paths, but all are thirteen steps long, not including that first alpha decay) for total of fourteen steps before it gets to lead-206.
[Check this one too. The difference in mass numbers is 238-206=32; dividing by four that is eight alpha decays. But eight alpha decays reduces the number of protons by sixteen, so if that’s all that happened uranium-238 would become osmium-206. (Uranium is element 92; 92-16=76; 76 is osmium.) In order to actually end up with lead (82), we need to, somewhere along the way, get six additional protons; we do that with negative beta decay (β–) which turns a neutron into a proton. So six beta decays are needed. Eight alpha decays + six negative beta decays = 14 total decays.]
Is this huge number of decays a problem? In principle it could be, but in this case it’s not. The initial uranium-238 to thorium-234 decay is very slow, with a half life of 4,468,000,000 years. Compared to this the others are practically instantaneous, with uranium-234 to thorium-230 requiring 245,000 years and thorium-230 to radium-226 requiring 75,400 years. Radium-226 to radon-222 has a half life of 1600 years. All of the other decays happen in less than a year and some take less than a second. So, basically, once a uranium-238 atom cuts loose and spits out an alpha particle, it’s going to be a lead-206 atom in less than a couple of million years, tops; which in comparison to the half life of uranium-238 (4,468 million years) is negligible.
Half Lives and the Radioactive Decay Equation
So, let me remind you about half lives. This is the amount of time it takes for half of the atoms in the sample to decay. It’s a little tricky wrapping one’s head around this at first. Surely, if half of the atoms are gone in 4,468 million years, the other half ought to be gone in another 4,468 million years. But it doesn’t work that way.
Each atom is independent of the others, and any given U-238 atom has a totally random 50 percent chance of going “kablooey” sometime within the next 4,468 million years. It could be right now while you’re watching it, or it could be 4,467.999 million years from now. If it doesn’t happen between now and then, guess what? You are still looking at an atom that has a 50 percent chance of going “kablooey” in the next 4,468 million years. The past history doesn’t matter. If the atom is 100,000 million years old already, versus created last year, it still has the same changes of blowing up in the same period of time.
Go to multiple atoms in a sample; billions, trillions or quadrillions of them [a one-gram sample of uranium-238 has 2.53 sextillion (or 2.53 trillion billion) atoms in it]. Since each individual atom has a 50 percent chance of blowing up in the next 4,468 million years, half of them, you don’t know which ones in advance, but half of them will do so. OK, so let’s say your very distant descendant takes your one gram sample and separates out all of the lead and intermediate decay products (the other things on the chain), and he has half a gram of uranium-238. His past does not matter; he has a half-gram sample of uranium-238 and half of it will decay in the next 4,468 million years, leaving his distant descendant with a quarter of a gram of uranium. (And maybe by that time an honest Leftist will have been born.)
The following GIF is a simulation of radioactive decay, with four samples each of four and four hundred atoms. The number at the top is the number of elapsed half lives. (It runs a bit fast unfortunately, so watch closely.)

Another way to talk about it is to say that, for a given isotope, the number of decaying atoms in some time interval is proportional to the current number of atoms.
In fact since the decaying atoms reduce the size of the sample, the number of decays is the rate of change of the size of the sample. Twice as many decays? Twice as fast a reduction.
In order to truly understand radiometric dating we have to understand this, and be able to express it mathematically. And I want you to truly understand it.
Intense Math Alert! Go to the bolded paragraph below to skip this.
Expressing this semi-mathematically, using ∝ for “is proportional to”:
(Number of decays in a specified time interval) ∝ (Current size of sample)
Or:
(rate of change of the sample size) ∝ (Current size of sample)
Or a bit more formally, with N(t) being the number of atoms in the sample at time t, expressed in calculus notation:
−dN/dt ∝ N
(The negative sign is because the change is in the downward direction, yet we will want to use a positive constant when we introduce it shortly.)
Or we can make it an equation by creating a proportionality constant, λ, (Greek lower-case lambda); in this case it’s called the decay constant.
−dN/dt = λN
And rearrange just a bit:
dN/N = −λdt
Welcome to the world of differential equations. This one is easy to solve, since the only way a function can be its own derivative is if the function is et, and if you want a function to be its own derivative but multiplied by some number is for the function to be something like ekt., in which case the derivative will be ket. So taking advantage of this fact, we get:
Key Equation: N(t) = N0e−λt
Where N0 is the size of the sample at some particular time, and N(t) is the size of the sample at some earlier or later time, t.
[e is the base of the natural logarithms and I talk about it (and logarithms) here: https://www.theqtree.com/2023/05/20/2023%C2%B705%C2%B720-joe-biden-didnt-win-daily-thread/ and here: https://www.theqtree.com/2023/06/17/2023%c2%b706%c2%b717-joe-biden-didnt-win-daily-thread/.]
This concerns the so-called parent nuclide. The daughter product increases, of course. What’s the formula for that? It’s convenient that the number of atoms does not change; even if fewer and fewer of them are the parent isotope. In other words, the total number of atoms, parent + daughter, is always N0 no matter how much (or how little) decay has happened. That means that to get the number of daughter atoms, you can simply subtract the number of parent atoms from the original number of parent atoms. I’m using subscripts p and d here to indicate number of parent and daughter atoms
Nd(t) = N0 − Np(t)
Substituting in the Key Equation for Np:
Nd(t) = N0 − N0e−λt
But this just begs to be simplified a bit:
Nd(t) = N0(1 − e−λt)
Earlier I was talking in terms of half lives, but we don’t see that here; we see this funky lambda constant instead. Can we get to a formula that uses half lives?
Yes but before we proceed I should say something about λ. We’re eventually going to want to put an actual numerical value on it, but it’s important to note that this is a number that applies to some given time interval. A second, a year, a million years. This number is actually the fraction of the sample that decays in whatever time interval you choose. So if a trillionth of the sample decays in one second, λ is one trillionth (0.000000000001), but to express that in years, you need to multiply it by 60 × 60 × 24 × 365.25, and if you want it to express it for millions of years, you have to multiply it again by another million. In this case we’re dealing with geology and our λ values will be set for million-year units.
The first step is to simply invert λ, defining a new constant τ:
τ = 1/λ
This gives you the average lifetime for an atom of the parent isotope, in whatever unit (seconds, years, millions of years, whatever) that you used for λ.
Note that this is not the same as half life. Half life is the time it takes for half of the atoms to go kablooey, but that’s not the average time it will take for one to do so. Some atoms ( one in 1024) will survive ten half lives, and they pull the average up. But it’s easy to get to the half life, t1/2 from here–multiply by the natural log of 2 (about 0.693):
t1/2 = τ ln(2) = ln(2) / λ
The reverse process:
λ = ln(2) / t1/2
And it turns out that there’s a version of the Key Equation with the half life…actually two versions that are equivalent to each other.
Cumbersome Half Life Key Equation: N(t) = N0e−ln(2)t/t1/2
This is ugly so it gets simplified as follows:
Simple Half Life Key Equation: N(t) = N0 2-(t/t1/2)
This one is intuitive in terms of half lives. Raise 1/2 to the power of the number of half lives that have elapsed to get the fraction of atoms remaining, then multiply by the original number. Or equivalently raise 2 to the negative power of the number of half lives.
So do we prefer working with λ or with t1/2? Scientific calculators come with an ex key; they never come with a 2x key–which forces us to work with that cumbersome formula above if we want to use half lives. (Honestly I’d write a program if it were a programmable calculator: store the half life in memory, and input the time, let the program do all the steps in the Cumbersome equation.) On the other hand I am having a very difficult time finding a table of isotope decay rates; half lives are easy to find.
END OF INTENSE MATH but be aware there will be a lot of applying the equations from here on out. That’s basically arithmetic, though, not differential equations.
For those of you rejoining us here, I’m going to repeat the formulas and definitions:
Decay Rate Key Equation: N(t) = N0e−λt
Cumbersome Half Life Key Equation: N(t) = N0e−ln(2)t/t1/2
Simple Half Life Key Equation: N(t) = N0 2-(t/t1/2)
N(t) is the number of atoms of the parent isotope (the one that’s decaying away) at any given time t. N0 is the original number of atoms of the parent isotope.
t1/2 is the half life. λ is the decay constant, the fraction of the sample that decays in some specified time (seconds, or millions of years, as appropriate). Dividing 1 by λ gives τ, the average lifetime of an atom in the sample.
I rarely see λ used. But for uranium-238 it’s: 4.916 x 10-18 (when working in seconds) and 1.551 x 10-10 (when working in years). If you use the latter number you need to supply t in years, not seconds–which, let’s face it, is more likely what you want to do anyway. In fact, this is geology (or have you forgotten?): You probably want millions of years, in which case λ for uranium-238 is 1.551 x 10-4.
In fact, let me supply the numbers for U-235, U-238, and thorium-232, since we’re going to be mentioning them at some point below.
Isotope
U-235
U-238
Th-232
Half Life (My) t1/2
704
4468
14,050
Decay Rate λ
984.6 × 10−6
155.1 × 10−6
49.33 × 10−6
(I here took the liberty of using “engineering” numbers rather than strict scientific notation (where the power is set so only one number is left of the decimal point) so that you could compare the decay rates more readily. The engineering mode uses powers that are multiples of three so it’s easy to write out a metric prefix, e.g, 1.32 × 104 watts (scientific notation) becomes 13.2 × 103 watts (engineering notation) or 13.2 kW (very readily read off the engineering notation).)
OK, there is some more math but at least I’m not slinging differential equations any more:
Determining Age (The Simple, Ideal Case)
Since we are dating a sample rather than predicting how much will be left after some time, these formulas are backwards. Instead of telling us how much is left after a known time has elapsed, we expect to know how much is left, and want to know how much time it took to get to that point.
Rearranging the Decay Rate Key Equation we get:
t = ln(N/N0) / –λ
or, getting rid of the minus sign by taking the natural log of the reciprocal instead:
The Dating Equation: t = ln(N0/N)/λ.
(“ln” is the natural log; the logarithm to the base e.)
OK so how do we apply this?
In principle, we can analyze some rock to determine how much U-235, Pb-207, U-238, Pb-206, and for bonus, Th-232 and Pb-208 is in it. We will want to know numbers of atoms–or at least the ratio of the number of atoms, not weight, but it’s easy enough to convert. We can then use the last formula above three times, remembering that (for the U-235 case) N0 is actually the sum of the U-235+Pb-207 numbers, whereas N is just the U-235 count. So you have two (or three, if you are checking thorium as well) pairs of numbers; run the calculation with each one. You now have three answers; if they are all the same, you’re in business.
Here’s an example: A rock that happens to be 704 million years old. You don’t know this (real science doesn’t have the answers in the back of the book), but you want to, so you take a tiny sample. For now we’ll assume no pre-existing daughter nuclides, no losses of any atoms over time from the sample, and no contamination of the sample. You put that sample into a mass spectrometer, which vaporizes the sample, ionizes the atoms, and sends them past a magnet at high speed. The atoms, being charged, will follow curved paths past the magnet. Heavier atoms will be bent less by the magnet. We put a detector downstream and it notes how many atoms hit where an atom of mass 206 should strike. Also for 207, 208, 232, 235, and 238.
What does our scientist see? It so happens I picked that number for a reason; it’s the half life of U-235. So our scientist will see equal numbers of U-235 and Pb-207, say 5 million of each. It doesn’t matter, it’s the ratio between the two that matters, and in this case it’s 1:1. That will probably make him smile because he won’t even have to pull out his calculator for that one–he will already know the answer. But he decides to check that, so what about U-238 and Pb-206? He will see 11.54 atoms of Pb-206 for every hundred atoms of U-238. Say, 1 billlion atoms of U-238 and 115.4 million atoms of Pb-206 But in order to use the formula above, he needs N0/N, the ratio of the remaining parent atoms (1 billion) divided by the total number of atoms involved in this (parent + daughter), to the number of remaining atoms. So what he wants is (1 billion + 115.4 million)/1 billion = 1,115,400,000/1,000,000,000 = 1.0577. When he plugs that into the dating equation t = ln(N0/N)/λ, being careful to use the value of λ for U-238, he gets 703.98 million years. Now he’s really happy because his numbers match. If he checks Th-232/Pb-208 he’ll get (regardless of the actual amounts) 3.534 atoms of lead-208 for every hundred atoms of thorium-232. Using this, he gets N0/N of 1.0353, divides by λ for Th-232 (49.33 × 10−6), hits the ex key on his calculator…and the age comes out as 704.1 million years. Now he’s grinning ear to ear, because he took three sets of measurements, independent of each other, and got the same result every time. What could be easier? (Actually a lot of things could be easier; actually analyzing the sample in order to get those six numbers is painstaking work.)
That’s the third grade version of what is called “uranium-lead dating.”
[In the light of a joke Pat Frederick made last time, uranium-lead radiometric dating is when her father shoots you full of lead or depleted uranium because he caught you shooting his daughter full of something else. But that’s the high-school level version.]
How To Deal With Non-Ideal Cases
I said this was the third grade version. That’s because I made a bunch of assumptions for this case. I said so before, and now I am going to repeat them.
- No initial daughter nuclides (in other words the rock contained no lead when it was formed).
- Neither a) any lead nor b) any uranium (or thorium) leached out of the rock since it was formed, since that will mess up our ratios when we measure them.
- No contamination of the sample either from natural processes or as it is collected and analyzed.
The problem is when dealing with rocks it’s never that tidy, though it can get close. We cannot simply assume that the sample started out with no daughter isotope in it. Or make any of those other assumptions, at least not without justification.
So when uranium-lead dating is done (in the lab, not in her house), it’s usually done with the mineral zircon. The chemical formula for this is ZrSiO4. It’s a silicate of zirconium, element #40. Here is an insanely nice specimen of zircon:

But hold on here. There’s no uranium in this mineral!
There’s no uranium, if it’s pure. However these crystals form in a mass of molten rock (magma), and this is Planet Earth unfiltered and unpurified. There will, therefore, almost always be impurities in it. (This is why pure white diamonds are very valuable; they have little to no impurities in them and that is a rare situation indeed.)
Zircon crystals will form in any igneous rock as it solidifies from magma. In fact, they’re practically the first thing that will form. (This is good because it’s easier for a crystal in still-liquid medium to reject impurities than it is, if almost everything surrounding it is already solidified.) They typically end up being the size of sand grains, and so any sizeable igneous rock will have a number of them in it. Zircons are also harder than quartz, with a Mohs hardness of 7.5 vs. quartz’s 7.0. (They will scratch steel and glass.) Which means they will be hard to damage, and can erode out of an igneous rock and end up incorporated in a sedimentary rock, essentially undamaged.
As it happens, if there is any uranium (either isotope, it doesn’t matter because we’re doing chemistry at the moment) in the magma, it can be incorporated in the zircon quite readily. So can thorium. The uranium atoms end up as part of the crystal, replacing some of the zirconium. But the cool thing about it, and the reason we want zircon crystals, is that lead is rejected as the crystal forms. So the innards of the new crystal will contain some uranium, and no lead whatsoever.
Furthermore, uranium won’t leach out of the zircon crystals over time.
That’s handy! And sedimentary rocks will have the crystals too, once they erode from igneous rocks. The thing to remember about the crystals in sedimentary rock is that dating those crystals will not give you the age of the sedimentary rock, but rather the age of some igneous rock that eroded, the grains from which became part of the sedimentary rock. They will put a maximum on the age of the sedimentary rock, but no minimum (maybe it formed last Tuesday).
This is a bit of a pain, because we find fossils, including index fossils, almost entirely in sedimentary rock. It’s not insurmountable, but that’s a topic for a future post. For now let’s stick to igneous rock.
If we take care to use the innards of the zircon crystal, rather than the surface, and run our lab like a clean room, we can reduce the possibility of contamination. If there is contamination in spite of all of these, we won’t get consistent answers (as we did in our example above) and can just disregard the results from that sample.
We’ve taken care of every assumption, except for 2a: We don’t know whether or not any lead leached out of the crystal after it was formed. And that does happen. Zircon crystals don’t like lead, so they’ll push it out if they have a chance, while hanging on to the uranium and thorium that’s still left.
One thing that can cause this is if the zircon is heated to over 900 C after it is formed, like happens when the rock it is part of is transformed into a metamorphic rock. Also, ironically, the uranium’s radiation can actually damage the crystal as it decays, allowing lead to leak out at lower temperatures. (And remember, every uranium-238 atom that decays emits radiation fourteen times!)
OK so how do we deal with this?
Let’s go back to our example of the 704 million year old unicorn rock that had no issues with it. Make it a rock with some number of zircon crystals, and we’ll use the crystals.
The crystals will all have different rates of lead loss, slightly different but different enough for this to work. So let’s take a specific crystal, and let’s say it has lost fifty percent of its lead.
How does a scientist use this to date the rock?
Let’s first see what he measures.
In our previous example, the scientist saw 5 million atoms each of U-235 and Pb-207. This time, though, unbeknownst to the scientist, half of the lead leaked out before the sample was collected. So what he sees instead is 5 million atoms of U-235 and 2.5 million atoms of Pb-207. It looks like N0 is 7.5 million (not 10 million) so he does the division N0/N and comes up with 3/2 (instead of 2).
He plugs that into the Dating Equation:
t = ln(N0/N)/λ
using λ for U-235 and gets: 411.8 million years (probably rounding it to 412).
We happen to know this is wrong. He doesn’t.
Not yet, anyway.
Next, he works U-238 and Pb-206. This time he sees a billion atoms of U-238, but instead of 115.4 million atoms of Pb-206, he only sees 57.7 million. So he is dividing 1,057,700,000 by 1,000,000,000, and getting 1.0577. Plugging that into the Dating Equation with the decay constant for U-238, he gets 361.597…okay, 362 million years. Doing the same exercise with thorium (I’ll save you the gory details) yields an age of 355.1 million years, or 355 million.
These numbers are all over the freaking map. None of them are even remotely right…and this guy has been doing this sort of work for more than two weeks so he knows that this variation actually means he’s nowhere close, and he’s dealing with crystals that lost some of their lead.
What to do now?
Concordia Diagrams to the Rescue
Analyze another zircon crystal, and another. Let’s say the next one has only 40 percent loss of the lead. In that case the U-235 date is 477 million years, the U-238 date is 432 million years, and the thorium date is 425 million years.
He accumulates at least a few of these sets of data.
OK now the mathematical tool comes in. Bring out a sheet of graph paper and label the horizontal Pb-207/U-235 and the vertical Pb-206/U-238.
Before doing anything with the data collected, we have a bit of prep to do. We have to draw a line that shows the values where the two dates are in “concord” (agreement) with each other, and this will be called a “concordia diagram”
For instance, for an age of 100 million years, a perfect rock (like in my first example) will show 90.6 percent U-235 and 9.377 percent Pb-207. Dividing the two we get a ratio 0.1035. The same ideal rock would be 98.5 percent U-238 and 1.54 percent Pb-206. (We’re going to ignore the thorium for now), the ratio is 0.0156. So put a mark at 0.1035 on the horizontal and 0.0156 on the vertical. Label that mark “100.”
Do this for a bunch of different ages and you get this sort of curved line, with different points on the line labeled with different ages. It goes up to the right, but instead of being a straight line it bulges slightly upward.
Note this is a bit different from the graphs we made in Algebra 1. There, we had the independent variable along the horizontal axis, and the dependent variable on the vertical axis. This time we have two dependent variables, those two ratios, off of one independent variable (the age that would give those ratios under ideal circumstances). We are plotting the two dependent variables against each other.
(You don’t have to do all of this math every time, because the points are always the same. I would bet that it’s in tables. In fact, I wouldn’t be surprised if there was graph paper with this line pre-printed on it, though in the modern digital age that may have fallen by the wayside.)
In fact, I just used a spreadsheet to compute the values for 100, 200, 300…and so on up to 1000 million years, and plotted them. (I wasn’t able to get the spreadsheet to label the points.) In this case, 100 million years is at the lower left, and 1 billion years is at the upper right.
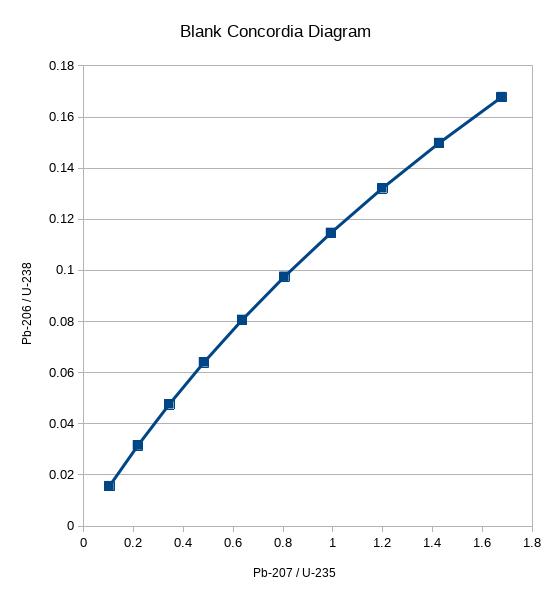
OK, now that you have this blank template, plot all of your measurements on it. For the first sample, there were 2.5 million atoms of Pb-207 and 5 million of U-235, so the ratio is 0.5. That’s your “x” value. And there were 57.7 million Pb-206 atoms versus 1 billion U-238 atoms, so the ratio is 0.0577. That’s your y value. Plot a point at (0.5, 0.0577)
Repeat for the other samples. These data points should lie along a straight line (if it’s not exact there are mathematical methods to find the “best fit” line). Extend it, and it will cross the curved line in two places. The upper right intersection represents the original ratios, you then can backtrack to figure out what age that point on the curved line represents. And you will get 704 million years, which is the actual age of the rock you pulled the zircon crystals from.
I can’t seem to get sample points onto the graph I just uploaded, but what I can do is show you an actual concordia diagram. This one was used to date rocks from the Klamath Mountains in Northern California. In this case as you can see the age is 461.17 +/- 31 Ma. (Spoiler: This turns out to be the middle of the Ordovician period. My example 704 million year old rock would, if real, come from the Cryogenian period.)
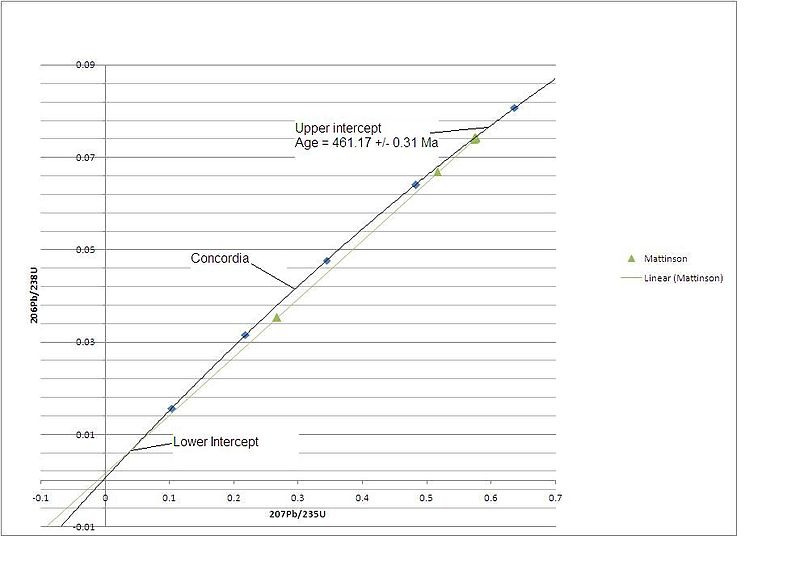
The upshot of this is, the concordia diagram lets you use the fact that there are two measurements to account for loss of daughter isotope, provided you can take multiple samples (with different amounts of loss) from the same rock.
What about the thorium-to-lead part? One could use Pb-208/Th-232 in a concordia diagram, instead of one of the two lead/uranium isotopes, but thorium decays more slowly so its ratios are smaller and a tiny variation in the measurement leads to a bigger variation in the date. The two uranium-lead numbers are more sensitive, so they get used instead.
There is a closely related method called Lead-Lead dating. I’ll cover that next time. Meanwhile, you’re probably wondering. What’s the oldest rock we’ve found?
Quit Holding Out On Us
The oldest “hit” found using zircons and uranium-lead dating so far is some zircon crystals taken from a rock in the Jack Hills in Western Australia, north of Perth. The crystals were found in a sedimentary rock, so the rock as a whole is younger than the zircons, which came out of an igneous rock that eroded a long time ago.
And that number came out to be: 4,404 +/- 8 million years.
Remember that this is a minimum age for the Earth. We’ll improve on it.
Here’s a picture of a Jack Hills rock:

It is believed that this rock (as a combined entity) is about 3 billion years old (that’s not a very precise number, but that’s the point; it’s hard to date sedimentary rocks), but obviously it’s made of older stuff, including those ancient zircon crystals.
I want to close by emphasizing that uranium-lead dating has been used countless times, and between that and other methods of dating I’ll be covering soon–also used countless times–we have built up a consistent notion of Earth’s age and ages for events during Earth’s “lifetime.” This isn’t a one-off that was then uncritically accepted.
Other, slightly newer zircons (4.3 billion years old) from the same area have had their oxygen atoms examined and the isotopic mix there (O-16 vs. O-17 vs. O-18, all stable) implies there was already liquid water on Earth’s surface.
And accepting these numbers isn’t a “presupposition” (as some people would claim) because the numbers are the results of a lot of evidence and scientific investigation.
If you want to dispute numbers in the millions and billions of years, you are going up against, quite literally, tons of hard evidence.
