Another week, another deluge of BS from the White House and from the Controlled Opposition. Not much has really happened, so with that noted, on we go.
On the plus side it looks like the Covid mask is slipping. A lot of places here are now saying no mask if you’ve been “vaccinated.” (And that’s based on the CDC, the governor has not dropped the mask mandate.) The COVIDschina goes on.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices
Gold $1831.70
Silver $27.54
Platinum $1257.00
Palladium $2980.00
Rhodium $27,400.00
This week, 3 PM MT on Friday, markets closed for the weekend
Gold $1844.90
Silver $27.53
Platinum $1232.00
Palladium $2949.00
Rhodium $27,600.00
Gold has broken out, but seems content to stay at this new higher level. Silver has not gone much of anywhere, down one cent. Platinum down (and it had to climb to close at this level today!). Palladium didn’t stay above 3000 for long, but perhaps it will punch through decisively soon, it too was climbing today.
Energy and Potential
(Part III of a Long Series)
Introduction
The general outline of this story is to start off by putting you “in touch” with the state of physics at the beginning of 1895. Physicists were feeling pretty confident that they understood most everything. Sure there were a few loose ends, but they were just loose ends.
1895 marks the year when people began tugging at the loose ends and things unraveled a bit. In the next three years, three major discoveries made it plain there was still a lot to learn at the fundamental level.
Once I’m there I will concentrate on a very, very small object…that ties in with stars, arguably the biggest objects there are (galaxies are basically collections of stars). And we would never have seen this but for those discoveries in the 1890s.
It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.
And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it…but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)
Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I used 9.8 kg m/s2 last time for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.
Revisiting Gravity with Vectors.
We now know something about vectors, and in light of that, we can go back a ways now to gravitation and take a look at it again.
The law of gravitation we discussed looked like this:
F = Gm1m2/r2
But force is actually a vector because it has a direction. This formula is full of nothing but scalars, so it only tells you the magnitude or size of the force vector, not its direction.
If you have a magnitude without a vector, then if you use it to scalar-multiply ia vector of length exactly one, you now have a vector of the right magnitude, because scalar multiplication changes the magnitude of the vector. And if that one-length vector pointed in the right direction, the new vector does too, because multiplying a vector by a scalar does not change its direction.
A vector of length 1 is called a “unit vector” and is a very useful part of the toolkit.
Sometimes it’s necessary to take a vector that isn’t a unit vector and determine the unit vector that matches it.
As you might have guessed, the way to do that is to take your vector, call it V, determine its magnitude, and divide it by the magnitude of V, which is to say, to multiply it by 1-divided-by-the-magnitude. (If multiplication is defined, so is division.)
There’s a symbol for the magnitude of V, and that’s to surround the vector by pairs of vertical lines, like this:
∥V∥
If you’re looking at a diagram, you can measure the vector off the diagram, but if you’re looking at something like [5,-12] how do you know its magnitude?
The answer is you square every element, add them together, and take the square root.
In this case, you’ll want the square root of 5•5 + -12•-12. Doing the arithmetic, you’ll want the square root of 25+144=169, which happens to be 13. So ∥[5,-12]∥ = 13.
This also works in three dimensions, consider [3,4,12], whose magnitude is the square root of 3•3+4•4+12•12 = square root of 9 + 16 + 144 = square root of 169 = 13 (again).
If you noticed something eerily familiar about this, that’s because this is also the Pythagorean theorem, the one about the square of the lengths of the legs of a right triangle equaling the square of the length of the hypotenuse. This makes sense, because the individual pieces of a vector are at right angles to each other.
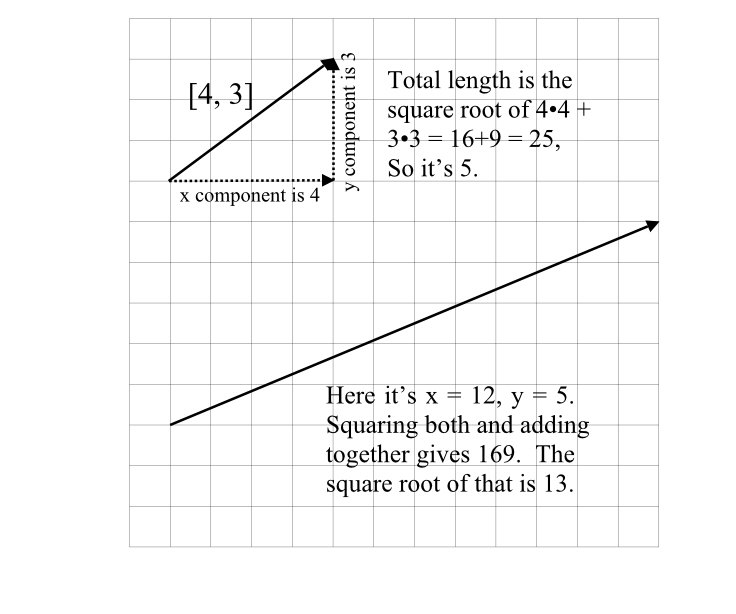
Now that you have your magnitude, you can divide your original vector by it to get a unit vector. So [5,-12], turned into a unit vector is [5/13, -12/13]. That vector has a length/magnitude of 1. A more common example is [3,4] which has a magnitude of 5. The unit vector is a nice tidy [0.6, 0.8].
So a unit vector corresponding to some vector V is V/∥V∥. Usually physicists and mathematicians will write the letter with a “hat” on it (for example, Â) to denote it’s a unit vector, but unfortunately not every letter has a version with a hat on it available in unicode (at least not on this machine), so I’m a bit constrained here. You might have to get used to the V/∥V∥ long form.
So let’s get back to gravity. We have the formula for the magnitude, how do we turn that into a vector? We multiply by some unit vector. Which unit vector? The one pointing in the right direction of course. (OK, smartass, what’s that?) We know that the direction of the force on an object due to gravity is towards the attracting object.
Let’s call the force by body 1 on body 2 F12. (Note the order of the subscripts, the first is the attracting body, the second is the attracted body.) The direction of that force is from body 2 back to body 1. So you can draw a vector, r21 from body 2 to body 1, unit-ize it, and you have your unit vector.
Actually, typically the vector is drawn from body 1 to body 2, the opposite direction, so we will write the formula in terms of r12. That vector is simply the opposite of the first one, it’s equal to -1 times the first vector.
r12 = –r21. Which of course means that r21 = –r12.
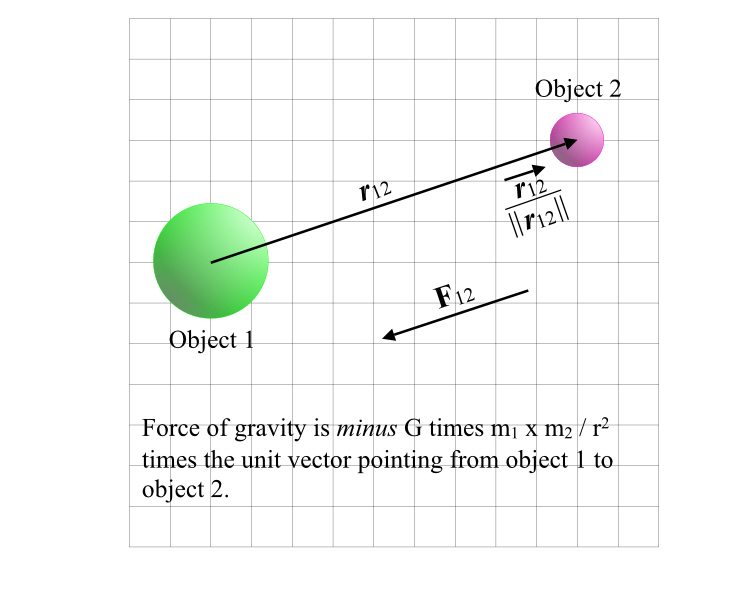
So we can write our vector version of Newton’s Law of Gravitation at last. (Edit: found an r-hat character!)
F12 = -(Gm1m2/r2) ȓ12
Notice the minus sign, which points the force vector back at the first object.
Energy
OK, so now we’re ready to proceed on to the subject of energy.
This is actually a concept that turns up again and again (and again, and Joe Biden didn’t win), in many different forms, the most basic of which is “work.”
Work, to a physicist, is what is done by a force acting on a body through a certain distance.
If I push on some object (on a frictionless surface, or out in space) and it moves some certain while I’m doing it, the work I’ve done is equal to the force I applied, times the distance.
W = Fd
Note that the distance traveled might not be due entirely to the push I gave the object. If it was already moving in that direction before I pushed on it, I’m still doing work on it by applying a force to it, even if most of the distance it traveled while I was pushing was due to the speed it already had.
(The key words are “in that direction”. If it’s moving at a 90 degree angle to the push I gave it, it has zero effect on the work done. I will have lots more to say about this, further on.)
So as a scalar, that’s just Work = Force x distance. But force is measured in Newtons or kg•m/s2. Working with metric units, that’s N•m, pronounced “Newton meters.” You can break it down further, since a Newton is a “kilogram meter per second-squared”, multiply that by “meter” again for the distance, and show that a “Newton meter” is also a “kilogram meter squared per second squared:
Work is measured in: kg•m2/s2
This is another named unit, the Joule, after James Prescott Joule, who in the 1840s performed a number of experiments showing that the sorts of energy we’re talking about today could be converted to heat (more on that later). The Joule in fact is the standard metric unit of energy.
So here’s a simple example. On Earth, a one kilogram object falling one meter, has 9.8 Joules of work done to it by the force of gravity. Let me back that up with the math. The force of gravity on that one kilogram object must equal its mass times the acceleration (F=ma); the acceleration due to gravity on Earth is g = 9.8 m/s2. (Little g is often used as a symbol for Earth gravity. Don’t confuse it with Big G, the gravitational constant or fudge factor from the first post in this series.) The mass is 1kg, so multiplying 1kg•9.8m/s2, the force is 9.8 Newtons, pointing straight down. (In fact, “down” is defined as the direction gravity pulls, so no coincidence.)
This is acting on the object over a distance of one meter, straight down, so it’s 9.8N x 1m = 9.8 N•m = 9.8 J.
It’s not just gravity. As alluded to earlier, you can push on an object, a rocket can push on an object. So long as it moves in that direction while you’re doing it, you’re doing work.
If you start at a standstill, and continuously apply the same force to an object, its acceleration stays the same. F=ma, or more to the point, a=F/m. The distance covered, d is equal to ½at2 (where t is the time you spent pushing it).
d=½at2
So if a is one meter per second per second, after you’ve spent one second applying the force, you’ve moved that object half a meter (½•1 m/s2 • 1•1s2 = 1m) = 1. After two seconds, you’ve moved the object two meters (½•1 m/s2 • 2•2s2 = 4/2 = 2m). After three seconds, you’ve moved four and a half meters (½•1 m/s2 • 3•3s2 = 9/2 = 4.5m). And so on. Basically, in this case square the number of seconds and divide by two.
If your object has a mass of one kilogram, the work done in the first second is 1m/s2 x 1kg x 0.5m = ½ of a Joule. In the second second, though, you travel one and a half meters (bringing the total up to 2 meters). So now the work done in that 2nd second is 1m/s2 x 1kg x 1.5m = 1½ Joules. So it seems like the longer you push the more work you do every second!
That moving object is now moving at 2 meters every second. And you’ve dumped a total of two Joules into it, working on it.
After three seconds, the total is 3 meters per second, and the work is 4½ Joules.
The work you’ve done on the object is manifesting itself as motion. Work is a form of energy, so is motion. Both are measured in Joules.
So let’s look at this again, cumulative totals:
t = 1 s d = 0.5 m speed = 1 m/s work done and KE = 0.5 J.
t = 2 s d = 2.0 m speed = 2 m/s work done and KE = 2.0 J.
t = 3 s d = 4.5 m speed = 3 m/s work done and KE = 4.5 J.
Notice the KE and speed match up like this: KE = ½v2. But actually, that doesn’t account for the mass. If you were to push a 2 kilogram mass with twice the force, the acceleration would be the same, but the work would double, and the kinetic energy the work does would also double. So the correct formula is:
KE = ½mv2
OK, a quick sanity check. I’m saying that kinetic energy and work are both forms of energy. One way to check that, is to look at the units. Actually, more precisely, the dimensions (distance, mass, time, rather than meters, kilograms and seconds). If the dimensions are different, they can’t be the same thing.
So: Work is force times distance. Force is mass times distance divided by time squared. So, combining, work is mass x distance / ( time x time ) x distance, or more compactly, md2/t2.
And kinetic energy is mass times speed squared, speed is distance over time, so combining, KE is mass x distance x distance / ( time x time ). Gathering things together, it’s md2/t2.
They match, so they could be equivalent.
And indeed they are, though I won’t be proving that here!
One thing I haven’t mentioned is whether energy is a scalar or a vector. It happens to be a scalar.
OK, let’s go back to that other 1kg object, the one that fell one meter and thudded onto the ground.
Let’s lift it back up one meter, back to where it fell from. Let’s do it smoothly.
While the object is being lifted, its speed does not change. Which is to say, it’s not accelerating. So the net force is zero.
But we know that gravity is always pulling down on that kilogram with a force of 9.8 Newtons. So for the net force to be zero, we must be applying a 9.8 Newton force upward.
Since we’re lifting the object one meter, the work we’re doing on it is
W = 1m • 9.8N = 9.8 Joules.
None of this is kinetic energy, though. What happened to the hard work? I’ll tell you presently.
In this specialized case of working against gravity, you can use a fairly simple formula for the work done:
W = mgd
Where g is the acceleration due to earth’s gravity, m is the mass, and d is the distance. But that’s not quite right.
To see why, let’s go to another scenario.
You’re pulling an object, say a hundred kilograms, up a very slick (frictionless) ramp (you’re doing this because lifting the dang thing straight up is hard!).
And you’re doing it smoothly, like with the lift of the one kilogram object, neither accelerating nor slowing down on the ramp.
If the ramp is 2 meters long, can’t you go back to your formula and figure out the work?
W = mgd
W = 100kg • 9.8 m/s2 • 2 m = 1960 J.
But that seems wrong. What if the ramp is almost flat? Versus a ramp that is almost vertical? If those are both 2 meters long, the vertical ramp is obviously more work!
If the 2 meter ramp is at a 30 degree slope, it turns out that the top end of it is 1 meter higher than the bottom end. (Thirty degrees is a “magic angle” in trigonometry. And if that means nothing to you just ignore it, as I’m trying to avoid trigonometry in these articles.)
Intuitively, what matters is the vertical distance traveled. Not the horizontal distance. And if you think about what work is, it’s applying a force. No force is being applied in the horizontal direction, because the object isn’t speeding up or slowing down and there’s no external force in that direction either, gravity points Straight Down.
So you need a way to take your motion as a vector, and use only the component of the motion vector in the same direction as the force to compute the work.
Because your motion and the force you’re countering are both vectors.
So what is the vertical height of the ramp? I just told you, it’s 1 meter. So 1 meter times the force of gravity gives you the right answer.
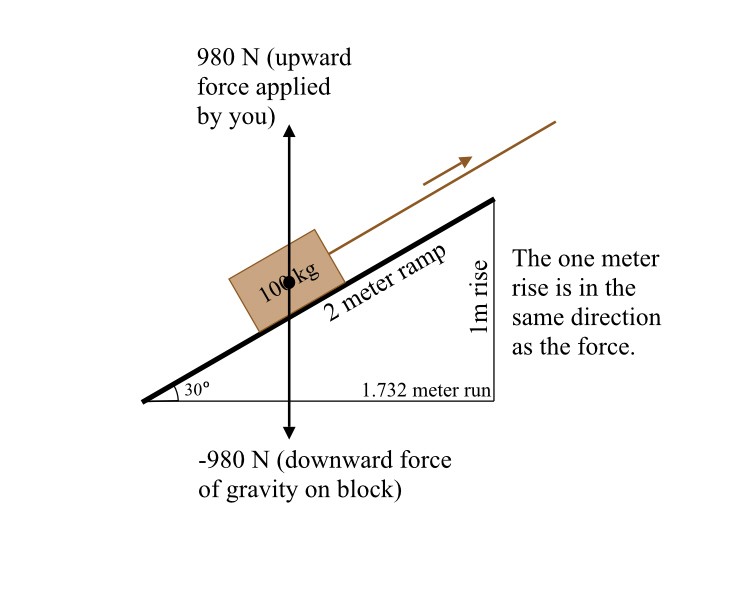
But there’s another way to analyze this! In fact, it’s probably a bit better. You could instead take the component of the force of gravity, in the direction of the slope of the ramp! After all that’s what you’re actually countering by pulling on the rope.
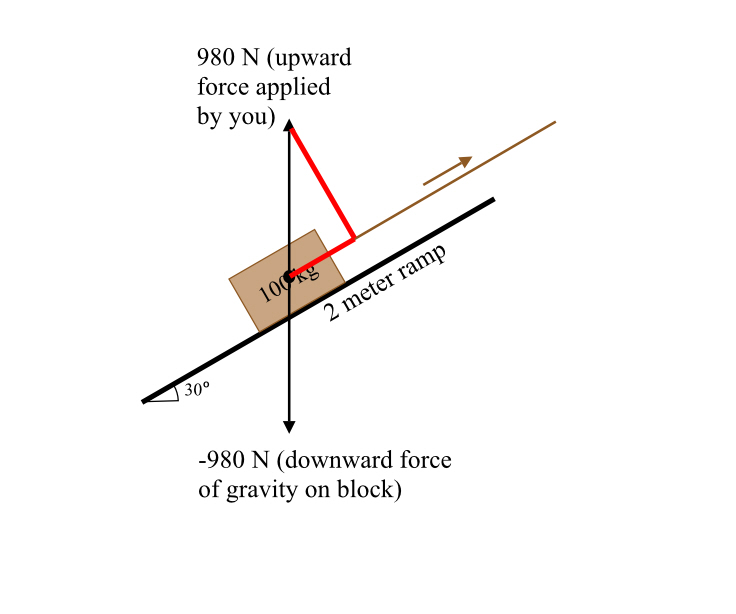
Note in red, the vertical vector is now broken down into an up-the-ramp component and a perpendicular-to-the-ramp component. Because 30 degrees is a magic angle, I know the force up the ramp is half the total, or 490N.
Now it is entirely appropriate to use the 2 meter length of the ramp, because it’s in the same direction as the force you are applying. 2m x 490N = 980J of work.
This is why ramps are useful, by the way. You can counter the force of gravity by applying very little force. In this case, half as much. The price you pay is you have to apply that force over greater distance, in this case twice as much. You could reduce the force as much as you want, if you have room and material for a longer and longer ramp.
Dot Products
Gee, it’d sure be nice if you could do this computationally. Well, you can. You can do trigonometry to determine that 1/2 factor for 30 degrees, or whatever it is for any other angle.
Gee, it’d sure be nice if you could do this computationally, without trigonometry. (After all, you don’t want to have to pester a geek and OMG! make him feel useful doing the trig for you.) Well, you can, if you have the vectors!
We do have them. The force we have to apply is [0, 980]N. The amount of distance is 2 meters, but we need the rise and run from the first diagram to be in vector form: [1.732, 1.0]m
[Trivia note: 1.732 is the square root of three (rounded to three decimal digits). Like I said, 30 degrees is a magic angle, the legs with a hypotenuse of 2 are 1 and sqrt(3). It’s easy to remember the square root of three because its digits spell out Washington’s birth year, 1732. If you’re a coin geek you can remember that because the Washington Quarter we use today began to be issued in 1932, his bicentennial. If you’re just a regular geek, you probably don’t know Washington’s birth year, but you probably do have 1.732 memorized and can use it to remember that Washington was born in 1732.]
OK, we have our two vectors, F=[0, 980]N and d=[1.732, 1.0]m
Here’s what you do. Multiply the first elements together, then the second elements, then the third elements (if you’re working in 3D), and if you’re playing 64 D chess, do the same for elements 4 through 64. Just keep going until you’re out of vector.
In this case, I end up with first elements: zero, and second elements: 980N•m. Done.
Add those numbers (all two of them here, all sixty four of them if you’re Donald Trump) and get, 980N•m.
You didn’t have to do any trigonometry! You didn’t have to break the vectors down into components, not in x-y or even along some cockeyed slant!
What we just did was to take the dot product of the two vectors, in other words we computed F∙d. That’s the real, vector form of the formula for work.
W = F∙d
Now I sometimes use a dot to show multiplication, particularly when I’m showing multiplying two actual numbers, or units. I’m having to use a big fat dot here, to distinguish the vector dot product from the just ordinary multiplier dot. (Note: It shows on my computer doing edits in a file, it isn’t showing up in the post editor, and may not show up as a big dot when it posts. We’ll find out, sometime before you read this!)
There are two things you may have noticed.
One, I’m talking about the dot product, not just the product; as if there were some other kind of product. With vectors, there is. Don’t worry…you’ll find out some future week! (Evil laugh!)
And another thing…the result of a dot product, is a scalar.
Work is a scalar. Kinetic energy is therefore also a scalar. Energy has no direction.
OK, let’s have a little more fun with the dot product. Take some vector, like v = [3, 4, 12]. Let’s take the dot product of it with itself, v∙v
That’s 3•3 + 4•4 + 12•12.
Does this seem familiar? Like maybe we did the exact same thing earlier in this marathon of post, while figuring out the magnitude of that exact same vector?
Except that when getting the magnitude we went on to take the square root. With the dot product we don’t do the square root. So the dot product of a vector by itself is the square of the magnitude. So, here’s a rule:
For any vector v: v∙v = ∥v∥2
Another rule. If two vectors are perpendicular, their dot product is zero!
I’m going to make up a four dimensional vector off the top of my head (I promise, I just made it up off the top of my head):
[12, -7, 9, -15]
I can make up another four dimensional vector and know that it’s perpendicular to this one, without having to draw a diagram. Which is good because my supply of four dimensional paper is a bit low right now. (The COVIDschina has caused all kinds of supply chain havoc.)
OK, let’s just make the first element of the second vector 9, and the second one 9 as well. You could literally pick any numbers for all but the last one. Make the third element -20. Let’s hold off a bit on the fourth one, and call it x.
[9, 9, -20, x]
I can take the dot product of this, it’s 108 + -63 + -180 + -15x, combining I get -135 + -15x, which has to equal zero if the vectors are to be perpendicular. It turns out if the last element is -9, the last bit of the cross product is +135 and the total is zero. (I was lucky, I didn’t end up having to multiply by an ugly fraction at the end.)
So even though I can’t draw a diagram of these two vectors, I know, like I know that 2+2=4, that [12, -7, 9, -15] and [9, 9, -20, -9] are perpendicular, because their dot product is zero.
If two vectors are parallel, but of different sizes, the dot product will be the product of their magnitudes. For example, [3, 4] and [6, 8] are parallel, because the second one is just 2 times the first one. Take the dot product, 3•6 + 4•8 = 18 + 32 = 50. If you do Pythagoras on those two vectors, their magnitudes are 5 and 10, which multiply together to make 50.
And that’s as far as I can take you without trig. There is a rule that tells you how big the cross product will be in terms of the two vector magnitudes and the angle between them…but, trig. (Fortunately the geeks here who know trig probably already know the rule.)
Potential Energy
OK, let’s return to the 100 kilogram block we pulled up the ramp, lifting it a meter, doing 980J of work.
In this case once we stop lifting the object isn’t moving. So our work didn’t become kinetic energy. What happened to it? It became potential energy. It’s basically stored in the object, as if it were a battery. To get it back, we drop the object, pretending to do so on some deserving Deep State puke’s head. (Maybe we can lay their picture flat on the ground.)
On earth, at least, we already have a formula for potential energy. It’s the work we put into it, the mass times the acceleration due to gravity times the distance. Only instead of d let’s use h for height, because that’s in the same direction as the force.
PE = mgh
where h is the height above the ground. Its distance times force, and force is in turn mass times acceleration due to gravity, g (9.8 m/s2).
So the object has potential energy. If you want the kinetic energy back, drop it, but then the object is back on the ground and the potential energy is gone.
(Note that we’ve been behaving as if the ground is the place where potential energy is zero. In fact, your choice of where zero is, is completely arbitrary. Imagine dropping the object down a well. If the potential energy is zero at ground level, it’s actually a negative number at the bottom of the well. As it turns out physicists like to put the zero point at infinity, and you’ll see why in a moment.)
It’s almost as if you can swap kinetic and potential energy freely.
Indeed, in many circumstances you can. If you don’t have to deal with friction, and other objects getting in the way, you can do it. One place where this is true is in space, there you only have to deal with gravity. In our discussion so far we’ve ignored everything else, so it won’t be quite accurate–you won’t quite get all the energy back when you drop the object, because of air resistance, no ramp is frictionless, and so on, but in space, there actually is nothing else.
An object’s kinetic energy, plus its potential energy, put together are called the mechanical energy and in space, for some given object in orbit, this is a constant.
So let’s look at kinetic versus potential energy in space.
Kinetic energy, we know how to deal with. But there’s a bit of a wrinkle with potential energy. On earth we deal with lifting an object a short distance, and the force of gravity is effectively constant over that distance. But when in space, you are not dealing with a constant force. Gravity measurably weakens the further you get away from Earth. So PE=mgh won’t work as a formula for potential energy. Instead, when dealing with potential energy with respect to the Earth, it’s –mmeG/r, with me being the mass of the Earth, G being the gravitational constant/”fudge factor” and r being the distance from the center of the earth. And as always, our object’s mass is m. If r is set to infinity, the potential energy is zero. As you get closer to the Earth, the number becomes more and more negative, reflecting less and less potential energy. This formula is only valid above the surface of the earth. Below the surface gravity again decreases. If the earth were a point mass, the formula would be perfect (and the Earth would be a black hole).
meG is also known as μe, the gravitational parameter of the earth, and that is 3.98×1014 m3/s2. So our potential energy formula is now:
PE = –mμe/r = – 3.98×1014 m/r
The earth’s radius is 6,378 km (through the equator, not elsewhere, but let’s use it), that’s 6,378,000 meters. So at the surface of the earth, the potential energy of a one kilogram object will be -62,402,000 Joules.
So it stands to reason that if you can give a one kilogram object 62.4 million Joules of kinetic energy, it will keep going until it’s an infinite distance away, having traded all of its kinetic energy for potential energy and bringing the potential energy up from looking like a millionth of the national debt all the way to zero.
Whatever that speed is, it’s the escape velocity of Earth. Impart it to an object on the surface, and it ain’t ever coming back!
Remember:
KE = ½mv2
But this time we know the kinetic energy and we want the velocity. So doing a bit of rearranging:
v2 = 2 KE/m
So simply multiply the 62.4 million Joules by two and divide by our mass of one kilogram, then take the square root. The square root of 124.8 million is 11,171.4 meters/second. That works out to 6.94 miles per second. And that’s our escape velocity, at least as seen from the surface of the Earth.
You can do this whole thing again with, say, a 57 kilogram object. The potential energy on the surface is 57 times as much (a bigger negative number), the KE is 57 times as much, but you divide out the mass. So the escape velocity is the same.
Now, let’s consider an object in a perfectly circular orbit. It will have a certain potential energy. It will also be moving at a constant speed. The sum of the potential energy and the kinetic energy, therefore will remain a constant.
But this is true in an elliptical orbit, too!
With an elliptical orbit, one end of the ellipse is as far away as the orbiting object ever gets away from Earth (the apogee, or more generically for any body, the apoapsis), the maximum potential. The other end is as close to the Earth as the object ever gets, the perigee or periapsis. It has a lower potential, which means the kinetic energy must be higher to make up for it. And indeed, if you’re in an elliptical orbit (around anything) you will speed up the closer you get to the object you are orbiting.
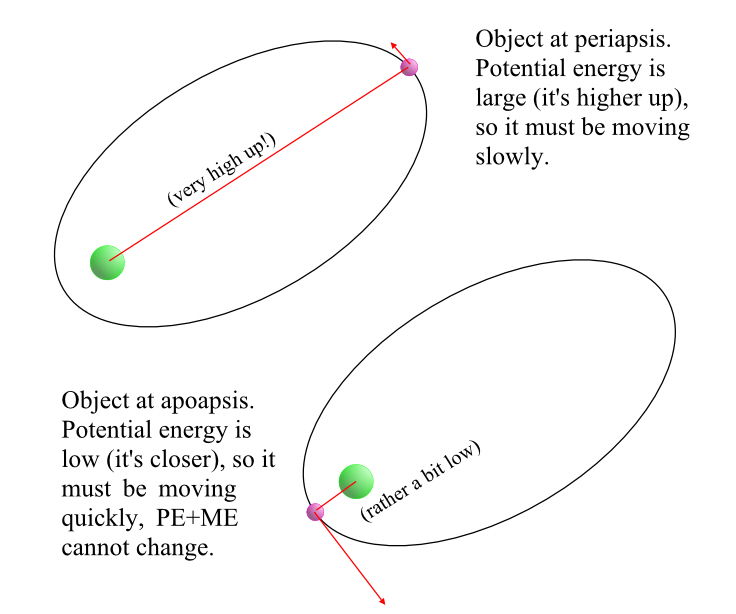
And in space, with no friction and no objects getting in the way, provided nothing comes along and disturbs that orbit, the object will go on circling, swapping potential for kinetic energy and back again, with perfect efficiency, forever. The mechanical energy, PE + KE, equals some constant. In fact, it’s zero if the object is moving at escape velocity, since PE + KE cancel each other out perfectly at that speed.
Something that doesn’t occur to most people. If the mechanical energy is zero, it will always be zero, and the object is always moving at escape velocity, no matter how far away it gets from Earth; it’s just that escape velocity is lower the further away you get. It also doesn’t matter which direction it’s going. It could even be going almost directly towards Earth. It’s still never coming back, as long as it doesn’t come so close to Earth that it collides with Earth. The one other thing you can say is that the path it traces will be a parabola.
When someone asks “what’s the Earth’s escape velocity?” they almost certainly mean “at the Earth’s surface.” So give them that 11 thousand something. But it’s different if you’re already ten thousand miles up!
If the mechanical energy is greater than zero, it’s not only going fast enough to escape Earth, it’s got surplus velocity to boot. (And it will travel in a hyperbola.) If the mechanical energy is less than zero, it will eventually reach a maximum distance and start coming back. It’s in a closed orbit, which will be an ellipse of some kind, a circle being the limiting case (all circles are also ellipses). The lower the total energy, the smaller the ellipse.
So under a certain idealized set of circumstances, mechanical energy is conserved.
What about other circumstances? Mechanical tends to bleed off, and decrease, especially that part of it that is in the form of kinetic energy. Think of a pendulum, that’s another “ideal” case of swapping kinetic for potential energy; the pendulum swings fastest at its low point, and is motionless at the top of its swing for a split second. It’s clearly trading potential and kinetic energy back and forth, over and over. But a pendulum is moving through the air, and air resistance will take a little bit of speed off that pendulum, so it won’t rise quite as far on the upswing. Over and over again, the pendulum swings less and less and eventually stops. It would go on longer in a vacuum, but the pivot point introduces some friction, too.
Friction is the nemesis of mechanical energy. The more friction, the more energy bleeds out of the system (unless it has no kinetic energy to begin with, think of a rock on a mountain top).
What happens to things when friction is going on? They heat up. So mechanical energy is being turned to heat.
Heat and Chemical Energy
As it turns out, heat is yet another form of energy. Our friend James Joule helped figure that out.
Heat, it turns out, is measured a bunch of different ways. The amount of heat necessary to raise the temperature of water one degree Celsius/Kelvin is defined as a calorie; a thousand of those is a kilocalorie (kcal), or sometimes Calorie with a capital C. That “big C” calorie is what you count when you’re on a diet, a food Calorie, and since heat is energy, it turns out that a Calorie of heat is 4,184 Joules. Chemists tend to use calories and kcal because they heat water a lot, then convert at the very end to Joules. They have 4,184 memorized. (I had to look it up.) It’s easy to work with calories when dealing with water. How many grams of water times how many degrees C you heated it up.
Not only is heat another form of energy, it’s the garbage can of energy. You can convert kinetic energy into heat, like by the energy of impact heating up whatever got hit, but you cannot convert all heat back into kinetic or potential, or any other kind of energy, only some of it. So energy tends to accumulate as heat over time, and this process is not completely reversible, so eventually all energy in the universe will be unharnessable heat. This is a consequence of thermodynamics. We’ll be out of usable energy. That is an energy crisis! Fortunately this is trillions of trillions of years off in the future, so you’d better do your taxes, but still, thermodynamics is the real “dismal science” because it tells us the universe is running down. You can’t win, you can’t break even, and you can’t quit the game.
This is also why any generating plant that relies on heat is not perfectly efficient. You burn the coal to heat the water into steam, you use the steam to turn a generator…but you can’t harness all the energy you put into the water and turn it into electricity, because that energy is all heat. Some is lost to practical use…forever. In fact a coal plant engineer would do cartwheels down the hall if he could get the plant to 35% efficiency. Two thirds of every pound of coal burned is wasted.
There is also energy in chemicals. That should be obvious by now since food contains kilocalories. Obviously, you can get that energy out by burning things. But it comes into play in another way. If you are James Comey, and you finally got your comeuppance and you’re having to make little ones out of big ones while waiting for your date with the executioner, you’re taking a big honkin’ sledge hammer, giving it a lot of kinetic energy, and smacking it into a rock, which breaks.
It take energy to break a rock. And that’s because the rock is full of chemical bonds that have to be broken, that’s a facet of chemical energy. The rock lost energy being formed, you’re resupplying it to break it back apart.
And when you eat bacon, you end up “burning” a lot of that fat for energy, and that is a chemical process.
A huge part of chemistry is tracking the energy through chemical reactions, supplying some where needed, using it where it’s given off. And reactions that give off energy and leave the reactants with less total energy tend to be favored; chemicals like having very little energy bottled up inside them. (There are plenty of added complications here; I won’t trouble you with them, but they are the reason paper doesn’t just burn spontaneously at room temperature.)
Conservation of Energy
OK, let’s take these other forms of energy into account (and others I haven’t even mentioned). What then?
You find that energy is conserved. In a closed system it is never created from nothing nor is it destroyed, though it can be converted from one form to another. So we have our third conservation law. We now have mass, momentum and energy conserved.
And that is another part of the state of physics in 1895.
Potential
I want to drop one more concept on you. The concept of potential. Not potential energy, just potential.
Consider a rock at the top of a cliff. It has a decent amount of potential energy, right? Another rock right next to it twice as massive has twice the potential energy. Or you could find a rock of the same size on a cliff twice as high. The point being that the potential energy depends on the vertical distance and the mass of the object.
Sometimes it’s very convenient to divide by the mass. When you do that with potential energy, you get potential energy per unit mass, also known as specific potential energy, or just plain potential. The two rocks at the top of the same cliff have the same specific potential energy, the same potential. But the rock at the top of the other cliff has twice the specific potential energy, because the cliff is twice as high.
You can turn potential into “how fast will that rock be going when it hits the ground, if it falls off the cliff” because that does not depend on the mass of the rock. Gravity accelerates all things equally, because the more massive the object, the more the force increases.
And with orbital mechanics, the satellite is usually such a tiny fraction of the primary’s mass, we divide the mass out of everything, turn the forces into accelerations, the potential energy into potential, and just square the velocity and divide by 2, because the mass of the satellite never changes, and if it does, so do the forces on it, it’s kinetic energy, and potential energy all in proportion. You’ve seen a hint of this in g being the acceleration due to gravity, not the force due to gravity. It’s more convenient to work with since the mass really doesn’t affect velocity, acceleration, or position.
I didn’t bring this up gratuitously. Potential will turn ot to be an important concept down the road, particularly when we look at electricity.
OK, now on to our 1895 mystery:
What makes the stars shine? (Introducing Power)
This is a big one. Almost everything we can see in the universe is a star. The planets here and out there are an insignificant fraction of the visible matter in the universe.
So if we can’t figure out the stars, in one respect we don’t know Jacques Schitt (or Adam Schiff) about the universe.
OK, so let me try to summarize what they had figured out in 1895. The stars shine, actually, because they’re hot. In the same way that embers in a fireplace glow. But stars are much hotter, the light they put out is whiter (true even for “red dwarfs”), and they put out a lot more of it. Physicists had done work on this “black body” radiation and could describe it really well, though they couldn’t figure out just yet why stars (and embers) didn’t radiate more at even higher frequences (bluer light and even ultraviolet)
But something that is glowing because it is hot, is actually shedding heat that way. Eventually it will cool off, stop glowing and assume ambient temperature.
So really, the question is what makes the stars continue to shine.
And that is a very good question. In order for a star to not just go dark, it must be accessing the same amount of energy every second that it puts out in that second. If it’s getting less energy, it will start to cool off, if it’s getting more, it will heat up. Most stars are fairly stable, so there must be a balance: energy radiated must equal “fresh” energy used to heat up the star.
We are talking about a rate of energy consumption, naturally expressed in Joules per second (J/s). That, folks, is power, and is measured in Watts. Yes, the Watts you know from light bulbs. Chances are good you didn’t know Watts are a metric unit!
The sun, to take a well known example, is pumping out 3.828 x 1026 watts. It’s doing so in all directions, so our little dinky Earth 150 million kilometers away gets only a minuscule fraction of it. Some of it hits other planets, the rest just blasts off into space, a ridiculously tiny fraction of it will hit other stars and their planets and maybe be seen by aliens.
Where does the sun get the 3.828 x 1026 Joules it needs every second to sustain this?
Let’s go over the possibilities that people had come up with. Chemical energy? What if the sun were a gigantic sphere of coal and it were being burned?
Well, we know how big the sun is, and we know its mass. We know how much energy coal releases when it burns. (We know that very well, since our economy largely depends on it.) If the whole thing were coal and were burning to pump out that kind of wattage, it would last 1500 years.
Which means the sun wouldn’t last the span of time since the fall of the Western Roman empire. Well, we have daylight now, and had it back then, so…scratch chemical energy. There are things that release more energy than coal, but not that much more; we can’t get from the pyramids to today.
But we already know kinetic energy can turn into heat, so what if a lot of meteors are hitting the sun, continuously? As it happens, if 1.2 x 1017 kg of meteorites were to hit the sun at its escape velocity every second, that would be enough to do it. That’s 120 trillion tonnes of stuff, every second!
But there’s no evidence that there’s that much junk hitting the Sun. Some of it would surely hit Earth and meteor strikes would be a lot more common than they are. Besides, this much mass falling on the sun would add one percent to its mass every 300,000 years. Increasing the mass of the sun increases its gravity, and we, monitoring planets orbiting the sun, would definitely know if this were happening, because the planets would gradually get closer to the sun and speed up in response to the mass change. Each year would be two seconds shorter than the year before, and there’s no way we’d miss that.
Finally, the best suggestion…though not good enough…came from Herman L. von Helmholtz in 1853. He was one of the people who first formulated the law of conservation of energy, so you can be sure he took that into account when making his suggestion. Why use meteorites, when the sun itself could be contracting and not gaining mass? If the material at the surface of the sun is in fact still falling towards the center, it’s converting potential energy to kinetic energy which can heat the sun up.
Helmholtz calculated that if the sun were shrinking 0.014 centimeters every minute, that would actually release the energy needed.
That works out to a mere 560 miles (out of a total diameter of 864,000 miles) in the roughly 6000 years of recorded human history, and again, this does not involve altering the mass of the sun at all. That total is a lot less since the invention of the telescope; small enough we could not have measured it as of 1895. (We’ve had more time since then, and our tech is better. Maybe we could do it today.)
So it looks promising. But running the clock backwards, the sun would have been big enough to swallow up the earth in its orbit at some time in the past, and that was calculated to be 18 million years ago. That’s a maximum age for the sun and especially the Earth, if that’s how the sun gets its energy. If it were any older than that, Earth wouldn’t exist today.
And that’s not nearly long enough. Geologists had plenty of compelling arguments that the earth must be hundreds of millions of years old, if not billions. And evolution needed time to act too. The theory had been put forward in 1859, and biologists were becoming convinced. Those were two independent arguments against a less-than-eighteen-million-year-old Earth.
So we have astronomers saying the sun can’t be that old, and geologists and biologists saying it must be that old. Who was wrong? Well, there was tangible evidence for the old earth, against physicists and astronomers not knowing how it could work; they were basically arguing from ignorance, and they knew it.
So they were willing to believe it was old, but that meant they had no idea what was powering the sun.
And that applied to all the other stars in the universe, too.
What’s powering the sun and every other star in the universe?
No one had any real idea, as of 1895. And remember, most of the visible universe is stars, and we didn’t understand them, so we really didn’t understand much, on a weight basis.
Obligatory PSAs and Reminders
China is Lower than Whale Shit
To conclude: My standard Public Service Announcement. We don’t want to forget this!!!
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!
