Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.
Not an Eagle
On my way to work there’s a large nest up in a half-dead tree, and I’ve been reminding myself to take pictures sometime. Well, I finally managed to do so and I established two things. 1) The autofocus on the camera I used sucks and 2) it’s not an eagle nest; it’s some sort of falcon with a white body. (The head is dark, even if it were an eagle it’d be a golden eagle, not a bald eagle.)
Postmodernism, a/k/a “Theory”
The other day I read a book review, regarding “Cynical Theories: How Activist Scholarship Made Everything about Race, Gender, and Why This Harms Everybody” by Helen Pluckrose and James Lindsay.
I must emphasize I have not read the book. According to the review, it doesn’t actually spend much time on many of the more politically noisome aspects of this latest version of “postmodernism,” but it is invaluable in going a step deeper in critiquing it than many others do.
A lot of the sheer nonsense pervading the Left is so crazy to anyone with a sane worldview that we find it hard to believe that the other side really believes this crap. But they do, because it is part and parcel of a nonsane worldview. And this broader worldview is discussed in the book. It makes Leftist nonsense seem at least somewhat sane within its own context.
We of course spend a lot of time here bashng “Critical Race Theory” (as it deserves) but other aspects of it are pernicious too and I thought I’d adapt the capsule summary of “Theory” I read in the review, here.
“Theory” apparently represents the latest wave of “postmodernism” which began in the 1960s with the work of Michel Foucalt. He argued that there is no such thing as objective truth. Or, if there is such a thing, it’s inaccessible to us because our knowledge is nothing but “narratives,” stories we tell each other and use to keep power.
Leaving aside the jokes playing off the fact that that statement itself is a claim to an objective truth, if there’s no such thing as objective truth, then basically anything goes.
Those two principles lie at the root of “Theory.” The next layer are four “attitudes” or methods.
- the blurring of boundaries between intellectual and social categories. This can result in anything from men wearing dresses to scientists relying on anecdotes.
- An emphasis on language as the tool that controls every aspect of life.
- Cultural relativism–not just in morality (e.g., cultures where behaviors we consider corrupt are considered normal, for instance) but even in epistemology. In other words the methods we use for figuring out the world around us are only valid in our culture. Some other culture can adopt other rules for determining, say, if gravity works.
- The lack of distinction between the individual and the universal. This means, among many other things, that “truths” (they insist on a plural there) have meaning only for a group. There aren’t any Steve truths, there are White Male truths. But there also isn’t a truth that is true for all of mankind either.
That’s the philosophic underpinning of today’s Left. No wonder they’ll believe such silly things.
It’s hard to predict what, exactly, the postmodernists will actually do with this, because as I said, these rules mean there are no rules for determining what is and isn’t true, much less what to do about a fact once it’s discovered. The PoMos themselves use bizarre jargon and revel in being incoherent. It’s a feature not a bug. And that’s a consequence of their basic beliefs. There’s no truth, “logic” is just one of many “ways of knowing” and one which must be tainted by racial/sexual/class bias…so what need to express oneself clearly or to give actual proof of one’s assertions?
Demanding that they be lucid is seen by them as a form of oppression; we’re trying to force them to use our standards.
Remember back in 1996 when Alan Sokal (a physicist) wrote a paper full of gibberish and it got accepted by a PoMo philosophy journal? The authors of this book repeated that in 2018, with over a dozen BS papers. One of those papers rephrased Mein Kampf in feminist jargon!
Cynical Theories makes the case that this stuff was apparently harmless up until the 1980s. The practitioners were unable to articulate an ideology, and couldn’t, therefore push to influence society. But in the 1990s they shifted gears. Keeping the two principles and four methods above, they fashioned a menu of separate specialist theories, e.g., “postcolonial,” “queer” and our current favorite, “critical race theory” among them, aimed at “deconstructing” things society used to take for granted, to show there was no objective truth there but just an attempt to hold power and oppress minorities. An example given in the review is “Disability and fat studies.” According to this even deaf or paralyzed people don’t suffer from their disabilities but rather from prejudice against them, held down by the network of power relations in society. So they argue that disabilities are yet another kind of “identity” and that trying to alleviate deafness or paralysis is actually oppressive and exploitative. And if a deaf or paralyzed person asks for help, he’s internalizing his own oppression.
Around about 2010 this garbage heap of “theories” coalesced into “Theory.” Collectivism is merged with the rejection of objectivity and now we have statements like “There’s no true truth but there are different truths for different categories of people.” Pluckrose and Lindsay explain “Having oppressed identities gives the oppressed a richer, more accurate view of reality-=hence we should listen to and believe their accounts of it.”
The dominant society, meaning, you guessed it, white male society, commits injustice against these groups when it fails to affirm their beliefs.
This is an inversion of Marxism, which claimed that the oppressed workers suffer from “false consciousness.” Now it’s the (alleged) oppressors who suffer from it, because they’ve been socialized to believe a certain set of “truths” that benefits them.
Special attention should be paid to the premise that language effectively constitutes reality, and blinds the majority to the fact that they are oppressing the minority. This accounts for one of the most aggravating aspects of the Left: They will insist on orthodoxy while simultaneously disowning their own efforts to enforce it.
And of course, this is why they conflate speech with violence. Because in their view, speech isn’t about reality, it is reality. A difference of opinion creates a power imbalance that threatens to erase a person’s only source of significance, which is other people “affirming” their “experience.” To listen, therefore, requires not just listening but actually affirming. Disagreement or criticism are inherently unjust.
There’s more, much more…I will probably be buying the book.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices
All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend).
Last week:
Gold $1844.90
Silver $27.53
Platinum $1232.00
Palladium $2949.00
Rhodium $27,600.00
This week, markets closed for the weekend at 3:00 PM Mountain Time
Gold $1880.70
Silver $27.63
Platinum $1172.00
Palladium $2834.00
Rhodium $25,500.00
Gold is doing very well. Platinum took a big hit, palladium fell 76 bucks on Friday alone, it’s now far away from its $3000+ dollar high point.. Rhodium is down, too, $1200 on Friday alone. Perhaps the PGM bubble is bursting? Realistically, it’s too early to tell.
Electricity and Magnetism (First Half)
(Part IV of a Long Series)
Introduction
The general outline of this story is to start off by putting you “in touch” with the state of physics at the beginning of 1895. Physicists were feeling pretty confident that they understood most everything. Sure there were a few loose ends, but they were just loose ends.
1895 marks the year when people began tugging at the loose ends and things unraveled a bit. In the next three years, three major discoveries made it plain there was still a lot to learn at the fundamental level.
Once I’m there I will concentrate on a very, very small object…that ties in with stars, arguably the biggest objects there are (galaxies are basically collections of stars). And we would never have seen this but for those discoveries in the 1890s.
It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.
And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it…but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)
Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I used 9.8 kg m/s2 last time for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.
A couple of go-backs.
I’m actually used to dealing with newtons, joules, and watts as abbreviations, N, J and W. Of course now I’m writing for an audience of about six people many of whom haven’t taken the same classes I have, and often spelling the units out. Ignorantly, I’ve capitalized them because their abbreviations are capitalized. That was wrong. Although the names of the people the units are named after are, of course, capitalized, the units themselves should not be. I knew this 40 years ago, I forgot. For example, “The metric unit of power, the watt (W), was named after James Watt.”
I beg your pardon for this error.
More substantively, I thought I’d say a bit more about the dot product.
And this time, I will reference trigonometry. Just a teeny bit. This won’t hurt…much.
Pictorially, a dot product of two vectors is equal to the magnitude of the perpendicular projection of one vector onto the other, times the magnitude of that other vector.
OK, that’s a mouthful! Let’s call our two vectors A and B. Last time around we defined a symbol for the magnitude of a vector, so that the magnitude of A is ∥A∥ and the magnitude of B is ∥B∥. But let’s also make one more convention, let ab be the magnitude of the projection of a onto b, and let ba be the magnitude of the projection of b onto a.
So a dot product of A and B is equal to ab∥B∥. But it works the other way, too, A•B = ba∥A∥.
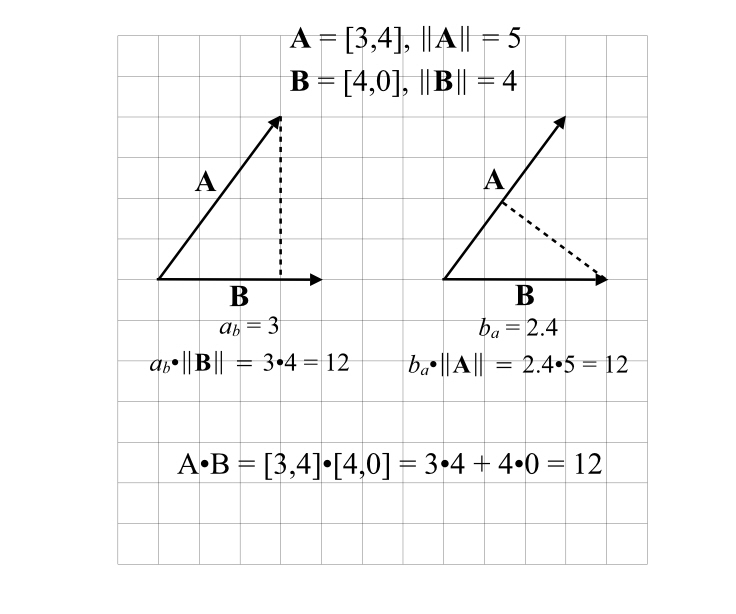
If you drop a line from the end of A to B, so that that line hits B perpendicularly, you’re said to have projected A onto B. In this case, the length of A‘s projection onto B is ab=3.
But you can also project B onto A, as in the second part of the diagram. When you do that, the length of the projection, ba is 2.4. I didn’t measure that, but I used ratios. The length of A is 5 (it’s part of a 3:4:5 right triangle), and the length of B is very obviously 4. The two triangles formed by the vectors and the dashed “dropped” line are similar, they share one angle where the two vectors meet, and a right angle, so all of the angles have to be the same. So if the hypotenuse of one is 5, while the other is 4, the other two sides must also both be cut by 20 percent. The projection of B onto A must therefore be 20% less in length than the projection of A onto B (which we know is 3), so that length must be 2.4.
In the left hand diagram, “the magnitude of the perpendicular projection of one vector [A] onto the other [B]” is 3. The “magnitude of that other vector [B]” is 4. The product is 12.
In the right hand diagram, these numbers are 2.4 and 5, respectively. The product of these two is also 12.
The dot product of these vectors is: [3, 4]•[4,0] = 3•4+4•0 = 12+0 = 12. So it works, at least in this example. I’ll let you look up the proof; I’ve only told you what it means.
What if both vectors are unit vectors? Since the vectors are of exactly the same length, their projections onto each other are the same, and since the vectors are of length one, the lengths of their projection onto each other will be one (if they are pointing in the same direction), or -1 (if they are pointing in opposite directions) or some number in between.
That number is the cosine of the angle between them, abbreviated cos.
The usual way of teaching trigonometry, shown in the first part of figure 2, involves drawing a “unit circle” (one with a radius of one), sticking this circle onto a Cartesian grid, and then drawing a line at some angle from the center of the circle to a point on the circle. Obviously the coordinates of that last point are going to differ depending on the angle, but the x value is the cosine, and the y value is the sine, abbreviated sin.
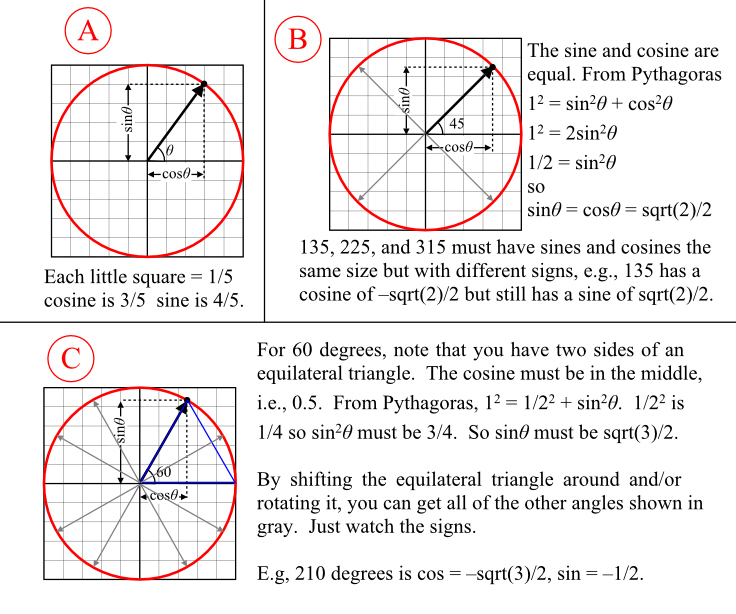
But you can look at the cosine of the angle as being the same thing as the projection of a unit vector onto a unit vector lying along the x axis.
Go back to my prior statement, about what a dot product was:
Pictorially, a dot product of two vectors is equal to the magnitude of the perpendicular projection of one vector onto the other, times the magnitude of that other vector.
With a pair of unit vectors being “dotted” together, both magnitudes in that sentence are 1. So, for unit vectors, it’s equivalent to
“a dot product of two unit vectors is equal to the magnitude of the perpendicular projection of one vector onto the other.”
But we just saw that the projection of one unit vector onto the other is the cosine of the angle between them. So if both vectors are unit vectors, the dot product of those vectors is the cosine of the angle between them.
If the first vector is not a unit vector, but is, say, twice as long then the magnitude of its projection onto the other is simply twice as long as well. In other words, that projection length is the magnitude of the vector, times the cosine of that angle.
You can go back to the original statement. The dot product of two vectors is the cosine of the angle between the vectors, times the magnitude of the first vector, times the magnitude of the second vector.
So the formal definition of a dot product is:
A•B = ∥A∥∥B∥cosθ
where θ is the angle between the two vectors.
This gives you a sneaky way to figure out the angle between two vectors. Take their dot product. Then divide by the magnitude of the first vector, and divide again by the magnitude of the second vector. You now have the cosine of the angle between them. You can look up the “inverse cosine” (i.e., the reverse of taking the cosine). Today, you can use a calculator (or calculator app). A few decades ago, a fancy slide rule might have a scale on it for cosines, from there you can look up the angle. Also you could look it up in a table. Sines and cosines are actually very well known functions.
There are a number of angles with well-known cosines that are actually expressable as somewhat-sane numbers. 45 degrees, for instance, is an angle at which the sine and cosine are equal, (see part B of figure 2). You can draw a right isosceles triangle there, which means the two legs are equal. Using Pythagoras, c2 = b2 + a2 for right triangles (with c being the side opposite of the right angle), and knowing that c = 1, and a = b, 1 = 2a2. So a2 = 1/2. Now a is equal to the cosine, or the sine in this case, so both are equal to the square root of 1/2, sqrt(1/2) (sorry, I can’t do fancy square root signs here). That’s 1/sqrt(2), but mathematicians hate it when you put a radical in the denominator, so they multiply top and bottom by sqrt(2) and get sqrt(2)/2. This is roughly 0.707. Similar reasoning will get you the sines and cosines of 135, 225, and 315 degrees, you’ll have to put negative signs in as appropriate.
60 and 30 degrees are other convenient angles. For instance with 60, you can get the answer from realizing that you can draw an equilateral triangle here, as shown in part 3. The X line, the slanted line, and a third line are all length one, and that’s a 60 degree angle there. It’s a symmetrical triangle, so the cosine has to be 1/2. The sine can be had from Pythagoras, too: sqrt( 1 – (1/2)2) = sqrt( 3/4 ) = sqrt(3)/2. Sqrt(3) = 1.732 (remember, Washington’s birth year), sqrt(3)/2 = roughly 0.866.
You can use similar reasoning for 30, 120, 150, 210, 240, 300, and 330 degrees.
Thes are all “magic angles” (as I called them last week) because you just know the sine and cosine and in some cases it’s even a nice nifty fraction like 1/2.
Most angles in whole degrees give you absolutely ugly sines and cosines.
OK, with that exceedingly gentle intro to trigonometry and the additional info on dot products out of the way…
Electricity
It has been known since at least 600 BC that amber (fossilized tree sap), when rubbed, could attract light objects. This was noted by Thales of Miletus. (There is no extant record on whether Thales had difficulty with the sheets coming out of his clothes dryer.)
Sometime in the next 2000 years, someone noticed that glass exhibited the same behavior.
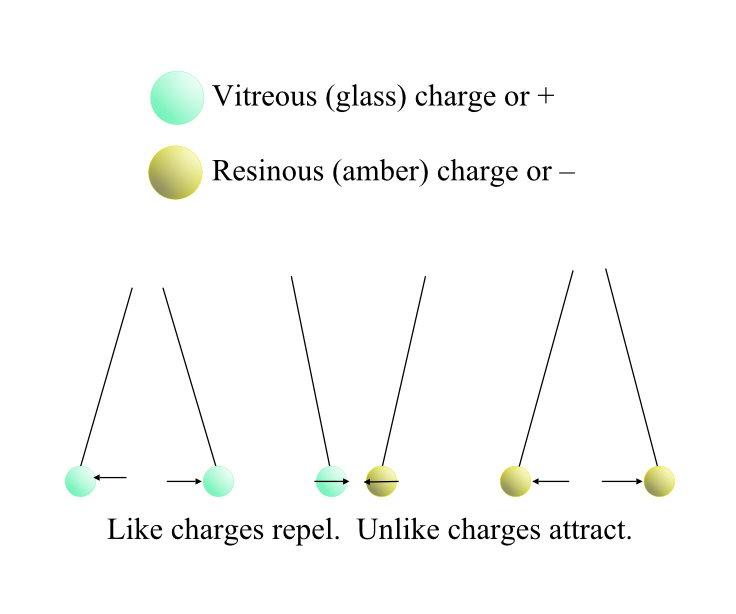
In 1723 Charles Francois Du Fay, a French physicist, realized that actually, glass and amber didn’t quite behave exactly the same way. Whatever it was they were doing was different in a rather interesting way.
Suspend two corks on silk threads. Buff up a piece of amber, touch one of the silk threads. The two corks are attracted to each other, somewhat. Buff up the piece of amber again, and touch the other silk thread. Now the corks actually repel each other, somewhat more strongly.
Whatever it is that’s in the amber that makes it attract small objects, when introduced to two different objects, caused them to repel each other, as if the whatever-it-is repels itself.
Repeat this experiment, but this time touch the second thread with a rubbed bit of glass. Now the two corks attract strongly. And if you repeat again, and touch both threads with the bit of rubbed glass, the corks repel each other again.
There is, in other word a resinous electricity (from amber) and a vitreous electricity, from glass, and they appear to be two different things, but able to interact with each other.
So vitreous electricity repels itself, but attracts resinous electricity (and vice versa), and resinous electricity repels itself too. They both seem to attract small things that don’t have any electricity in them at all. Like repels like and attracts the other.
At this point Du Fay came up with a fluid theory of electricity. Each kind of electricity was a different sort of fluid that would flow from solid object to solid object.
In the 1740s an otherwise obscure individual by the name of Benjamin Franklin in Pennsylvania did some more work. He was able to show that if you took an object with one of the two kinds of charge, and touched it with an object of the other kind, the charges disappeared, as if they had cancelled each other out.
Franklin came up with the single fluid theory. In this one electricity was a sort of fluid and under ordinary circumstances, an object would have a certain normal amount of it. But when it was in surplus, you saw one kind of charge, when it was in deficit, you saw the other kind. (In very similar fashion, surplus money can be used to pay off debt, a negative amount of money.)
And indeed this analogy suggests that the charge with the surplus of fluid could be considered positive, and the charge from a deficit of fluid could be called negative. This would be mathematically convenient. It wasn’t meant in any sort of pejorative way.
That is precisely what Franklin chose to do. However, he had no idea which kind was the surplus! He labeled the vitreous charge “positive” and the resinous charge “negative” and it has been this way ever since. His chances of getting it right (assuming a fluid was moving) were 50-50.
The charges could just as easily have been labeled black and white or red and green or yin and yang. But by Franklin’s time mathematical rigor had begun to pervade science, and so positive and negative, they were.
One difficulty with Franklin’s theory was that although one could imagine a fluid repelling itself (like two positive charges would do), but it was more difficult to imagine the lack of such a fluid in two objects creating a repelling force. Nonetheless, Franklin’s formulation was a lot more widely accepted than Du Fey’s.
One can also have different strengths of charges; one piece of rubbed glass might have twice as strong a charge as another. That, presumably, meant the first had twice as much of the fluid in it as did the second. Similarly, pieces of amber could have different deficits of the fluid. In order for charges to completely cancel out, it turns out, they must have equal magnitude but be opposite. If one is of greater magnitude than the other, then the result of the cancellation will be a slight amount of that charge, the leftover part that couldn’t be cancelled out by the other.
Imagine coming up with some way to measure charge, and you have a positive 3000 charge and another negative 2800 charge. Putting the two together, you’re left with a positive 200 electric charge, just like you’d get from adding the numbers +3000 and -2800.
There is in fact a unit of electric charge, the coulomb, named after Charles A. de Coulomb, and it seems to be a very large unit.
Who was Coulomb? He formulated the law of force between electric charges. This law superficially resembles Newton’s law of gravity. F12 is the force exerted by charge 1 on charge 2.
F12 = (kq1q2 / r2)•ȓ12.
As a reminder Newton’s law of gravity was
F12 = -(Gm1m2/r2)•ȓ12.
So instead of the masses, we have q, the electric charge of the objects, and we have a different constant, k. G was a small number, 6.67 x 10-11, indicating that two one kilogram masses a meter apart would attract each other with a force of 6 trillionths of a Newton.
The k in Coulomb’s law is 8.99 x 109. In other words, nine billion.
So two one Colomb charges a meter apart act upon each other with a force of nine billion Newtons. Which is almost the weight of a billion kilograms on earth, or about a million English-system tons. From one Coulomb acting on another.
As I said a Coulomb is a huge unit! The sheets in your dryer don’t stick to each other quite that hard, but when you remember static electricity can lift small objects against gravity, it’s pretty plain the electric force is likely inherently stronger than gravity.
Although Coulomb’s Law and Newton’s law of universal gravitation look a lot alike, with charge and mass filling in for each other, and different fudge factors, there’s one very important difference.
Newton’s law has a minus sign in it. Coulomb’s law does not. The minus sign serves to make gravity an attractive force, because it makes the force vector point the opposite way as the displacement unit vector. This doesn’t happen with electric charges.
But don’t we have situations where electric charges attract? Sure we do. And even though this formula describes a repulsive force, it does allow for this, because the result is negative when some part of the formula is negative; r2 must be positive, k is positive, so the only way that can be is if q1q2 is negative. If both charges are positive, the product is positive…and they will repel. If one is positive and the other negative, the product is negative, and it’s like gravity; they attract. Finally if both charges are negative the product is positive, and the two charges again repel each other.
So that’s how charges behave. It’s oddly like gravity and also oddly unlike gravity. And it’s a lot stronger than gravity.
Conservation of Electric Charge
It eventually became evident that electric charge is conserved. If your system starts out with 0 total, in other words, “electrically neutral,” you can create a charge somewhere in it, but always at the cost of creating an opposite charge somewhere else in the system–again, as if some amount of fluid had moved from one place to another. And if there is a charge somewhere in the system, it can only disappear if it’s combined with the opposite charge from somewhere else in the system.
What of the small objects…dog fur, scraps of paper, and so on, that are attracted to an electric charge, even though they’re neutral? For example, imagine dog hair stuck to positively charged glass.
We know the dog hair is not simply charged the other way. negatively, because it’s attracted to both kinds of charge.
As it turns out the electric fluid in the dog hair–it has some in it, just exactly enough to be neutral–is repelled by the glass’s positive charge, and ends up at the far end of the hair. Of course, this means the end of the hair closest to the glass now has a negative charge. And the negatively charged end is closer to the glass than the positively charged end is, so the attractive force is stronger than the repulsive force. Voila! The (overall) neutral object now sticks to the positive charge. Even if the hair is lying flat against the glass (and it probably is), the side touching the glass is closer than the side far away.
For the most part, the phenomena we’ve been talking about involves static electricity, electricity that is not moving. Sure, one of our experiments involved having it move along a silk thread. And there were also Leyden jars which could hold a substantial charge and would release it when the contacts were touched—sometimes enough charge to knock a man down. But for the most part, the charges didn’t move.
But electricity is much, much MUCH more interesting when it is moving, especially either steadily or in an oscillating fashion! More on that later; I have to set this aside and start another “thread” of thought now.
Magnetism
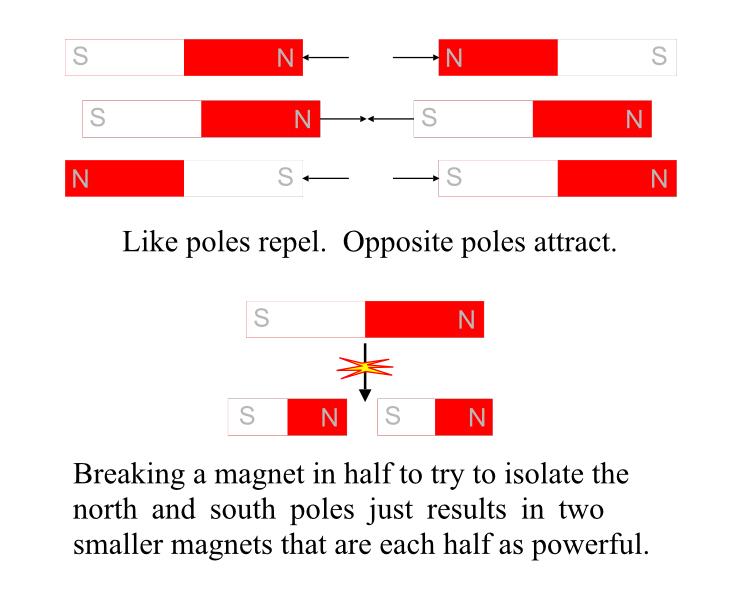
Another phenomenon, very similar to electricity in some ways and rather different in others, also turned up in ancient times. There were occasional rocks that would attract iron. They would also attract each other. But sometimes they repelled each other. And it turned out that the SAME rock would have a part that would repel the other rock, and one that would attract it. On the other hand, this didn’t matter when the rock was interacting with iron; either end would attract it.
This, of course, is what we now know as magnetism. And those two ends that attract or repel each other became known as poles.
That’s because a magnet, left free to swivel, will always point one of its two poles roughly toward the Earth’s north pole, that’s called the north pole of the magnet. The other is the south pole of the magnet. When it becomes a matter of representing these things mathematically, the north pole is considered “positive.”
Very much like electricity, similar poles repel, opposite poles attract. (Ironically, this means the Earth must be a giant magnet, with that magnet’s south pole near the north (geographic) pole, so it can attract magnets’ north poles.)
What happens if you break a magnet in half to try to separate the north pole from the south pole? You get two smaller, weaker magnets, each with north and south poles. The broken end of the north side of the old magnet is now a south pole, and the other side of the break is now the north pole of the other new magnet.
In fact, no matter how small you break a magnet, you will never succeed in having just one pole. This sort of thing, if it existed, would be called a “magnetic monopole” and it’s a true unicorn.
Magnets, too attract or repel each other in inverse propotion to the square of how far apart they are–which is mathematician speech for “there’s an r2 in the denominator.” This is hard to see or even use, though, because there’s always an opposite pole nearby which partially cancels things out.
Magnetic poles didn’t seem to move around within objects like electric charge does. But there was a sort of conservation law; in breaking a magnet in two, you still had equal numbers of north and south poles And the fact that there are no monopoles tells you that the total amount of “north pole” must be equal to the total amount of “south pole” because they always come in pairs.
Magnets, too, can be much more interesting when they’re moving.
Electricity Moving. Work and Potential
If there is a force, then work can be done.
Imagine an object, a kilogram in mass, with a coulomb of positive charge on it. Allow it the freedom to move. Put a fixed charge nearby, on an object that cannot move.
If you space things properly, that charged object will start to accelerate, at 1 meter per second per second. As if one newton of force were being applied to it.
That’s because there is a newton of force being applied to it, a newton of electrical force, not gravitational force, and not a solid thwack administered by an experimenter. And after a meter of this, the electrical force has done one joule of work, just like with every other kind of force.
In fact, you can draw an analogy here between the sort of potential we talked about, where the height of a cliff was related to how much work gravity would do on an object dropped off of it, to what the electrical force does to a charged object.
If, going from point A to point B, a coulomb charge has a joule of work done to it, the electrical (not gravitational) potential between A and B is one volt. Yes, that volt. Named after Allesandro Volta, about whom, more in a bit, and abbreviated with a capital V.
So the equation here is work = potential x charge. Double the potential, double the work; double the charge, double the work. Or 1J = 1V x 1C.
Equivalently 1V = 1J/C.
And similar to gravitational potential where twice as much work gets done by doubling the mass, you can get twice as much work out of a one volt potential, by having it operate on two coulombs.
Didn’t we just see that a coulomb is a gigantic charge? Or at least, that it exerts a very strong force, so big that no doubt we’ve never seen a coulomb out in the real world? What dang use is a volt? It must be pretty tiny to get only one joule out of a coulomb!
The fact of the matter is, though, that when electricity moves, a coulomb isn’t all that much, particularly if you can get it to move for a prolonged period of time.
This was quite a bit different from the static electricity games that people had been playing up to now. Sure, you could occasionally get static electricity to move (if not careful, it would move through you), but it would usually just do it all at once, and once it had moved there were no positive or negative charges. It was moving from a high voltage to a low voltage, all at once. Sort of like dropping a rock (hopefully not on your foot). Once the rock is at the bottom, you’re done getting work out of the system, and you’re done quite quickly.
Imagine, though, turning on a faucet and getting a continual stream of mass to fall. (Or imagine a waterfall.)
We figured out how to do this in the very late 1700s. The story starts with an Italian named Galvani in the late 1700s; he was dissecting frogs and noticed that a spark could make the leg muscles twitch, even though the frog was quite thoroughly dead. Then he noticed that if he touched it with two different metals, he could also make it twitch.
That was the clue that Allesandro Volta (1745-1827) needed. In 1799 he created something we now call a “voltaic pile.” Start with a disk of copper. Place on top of it a disk of cardboard soaked in salt water. Place on top of that a disk of zinc.
Run a metal wire from the copper plate to the zinc plate, and electricity will flow through it from the copper to the zinc. There’s clearly a “push” being given to the electrical fluid in the wire. That push is a potential of about 3/4 of a volt, but Allesandro Volta certainly didn’t call it that.
If you stack these, you can build up higher and higher voltages. Place another copper disk directly on the zinc one, another bit of salt-water-cardboard, another zinc disk, and the total is 1.5 volts. Do it again, and now you have 2.25 volts. And so on. As long as you put negative zinc right next to positive copper in your stack of these sandwiches, you build up voltage.
But the big thing is, electricity could now be generated chemically, and not just rubbing things together, and it was sustained for some period of time until this pile, what we now call a battery, ran down.
In just a few years, ending in 1808, Sir Humphry Davy was able to reverse things; instead of chemistry making electricity, he got electricity to do chemistry. He was able to isolate no less than seven elements from compounds that had previously proven to be too tightly bound to be broken by conventional chemical means. Up til then we were reasonably confident those elements were there; we just couldn’t actually prove it beyond a shadow of a doubt by getting those elements out of their compounds.
And as early as 1800 electricity from a voltaic pile was used to break down water into hydrogen and oxygen.
The thicker the wire, the faster the battery would run down. Almost as if more electrical fluid could “fit” in a thicker wire.
And now we have hit the concept of electric current. How much electricity is moving? That’s how much electric current there is.
One ampere is one coulomb flowing past a point, every second. It was named after Andre Marie Ampere (1775-1836). He did a lot of the early work on what he called “electrodynamics.”
If you look in your breaker box, you’ll likely see a lot of switches labeled 12, 15, 20 or even more “A”. That’s amperes, and when one of those breakers flips, you’ve drawn more than that many amperes through that switch. In a circuit whose breaker is labeled 12, twelve coulombs will pass through that breaker every second.
With all those coulombs moving around why hasn’t your house blown apart (or been sucked into a vortex) from all those coulombs attracting or repelling each other?
Because the electrical fluid moves, and it doesn’t accumulate anywhere. A coulomb flows from one side of the breaker to the other, but another coulomb of fluid is right behind it, so there’s no deficit to create a resinous/negative charge. And the fluid downstream from your breaker also moved on, leaving space for the coulomb that just flowed through the breaker. No accumulation, no net positive charge (and no places low on fluid to have a negative charge).
The wire forms a closed loop, with your house at one end, and a power source on the other, something that creates an electrical potential, so that current will flow from high to low. (This is sometimes called Electromotive Force, or EMF, and abbreviated with a script capital E: ℰ.)
In a battery the current is “pushed” by the battery through the wire, through whatever it is you’re using the electricity to operate, and back along another wire to the battery…which uses chemical energy to do work, and give it another push around the loop. So a battery converts chemical energy to electrical energy. Once it runs out of chemicals it can react, it’s dead. (This is another aspect of the conservation of energy.)
One difference between a battery and your house wiring is that in your house wiring the current switches direction, back and forth, sixty times a second (50 in Europe and some other parts of the world). This is called “alternating current.” A battery doesn’t switch back and forth, and it’s called “direct current.”
Digression
OK, I’m going to shift for a moment from physics to the metric system itself.
The newton, joule and watt are called “derived units.” They come from combinations of other, more fundamental units, the meter, the kilogram, and the second. Length, mass, and duration are very different things from each other, but force, for instance, has to do with mass, length and duration. But when it comes to electricity, we have yet another thing that’s different from everything else. So something having to do with electricity should be a fundamental unit. The metric system has seven fundamental units; we’ll probably only touch only two of the remaining three.
You would think that the fundamental unit for electrical things would be electric charge, but you’d actually be wrong. The “fundamental unit” having to do with electricity in the metric system is the ampere. The coulomb is defined as one ampere, flowing for one second (C = A•s); the volt is then defined as I stated above.
But it’s even a bit crazier than that. There are two metric systems! The one I’ve used all along is MKS, for “meter kilogram second” because that’s what it derives other units from. But there is an older, mostly disused system called “CGS” for “centimeter gram second,” it derives its unit of force, and energy and so on from centimeters, grams and seconds. Its unit of force is called the dyne—1 g cm/s2. When you consider that the gram is 1/1000th of a kilogram, and a centimeter is 1/100th of a meter, it should be no surprise that the dyne is 1/100,000 of a newton. The unit of energy is called the erg, and it is 1/10,000,000 of a joule. These are tiny, tiny units. The MKS units are easily “felt” by people: who hasn’t lifted 100 grams (weighing about one newton) about a meter and done a joule of work? But that’s ten million ergs!
Returning to Electricity…
OK, back to the main story.
Returning to our electrical circuit, from battery positive terminal through something that uses the electricity for energy, then back to the negative terminal of the battery, current is flowing.
What if there is a break in the wire? Won’t the electricity simply pile up?
Only the slightest, tiny bit. As more electrical fluid goes down the wire an unbalanced positive charge builds up, it begins to repel the fluid headed its way and forces it to a stop. This happens very quickly, effectlively, the current just comes to a screeching halt the instant the break happens. And if you measure the potential across both ends of the break, it’s now equal to the potential of the battery, whereas before the break, there was no potential difference at that point, but current was flowing through it.
Electricity is very eager to move, at least in good conductors; it really hates piling up, because a pile of it is a bunch of the same charge confined to a small space, and every bit of that repels every other bit, and hard.
Is there any constraint on how much current flows? Certainly. Every material, even a wire, has a resistivity to the flow of electricity. The more resistance, the less current will flow for the same voltage. On the other hand, if you double the voltage, that’s double the push, and twice as much current will flow through that same object. This works pretty consistently (until you reach the absolute carrying “ampacity” of the stuff and it heats up and melts or vaporizes, at which point, you’re done with that bit). Given a volt put across two opposite sides of a cube of the stuff, how much current will flow? Given that number, you can figure out how much resistance a certain object will have. It increases with length, and decreases with cross-section, so you can figure out the resistance of a wire, or any other object you want to carry a current, if you know the resistivity of the stuff it’s made of.
If the object the current is trying to flow through allows one amp through when it’s subjected to a volt, it has a resistance of one ohm, named after Georg Simon Ohm, who figured out that current flow was proportional to the applied voltage, and the proportion was different for every kind of material. In fact, it’s a law: the current through an object is equal to the voltage across the object, divided by the resistance.
I = E/R
I is current, don’t ask me why. E is from “Electromotive Force” and R is…wait for it…the resistance. Or to put it in metric units,
1 A = 1V/Ω
That funky symbol at the end is a capital Greek letter omega (as in “alpha and omega”), and perhaps it was selected to be the symbol for the derived unit ohm, as a sort of pun (ohm-ega).
If you have a circuit, from the positive end of a battery through three different resistances and back to the battery, you can measure the voltage across those three items and they will all have a pro-rata share of the voltage the battery is supplying. Say, for instance, it’s a 12V battery, and you have three lights hooked up to it, each light is 100 ohms. They’re all equal, and so the voltage across each light will be 4V.
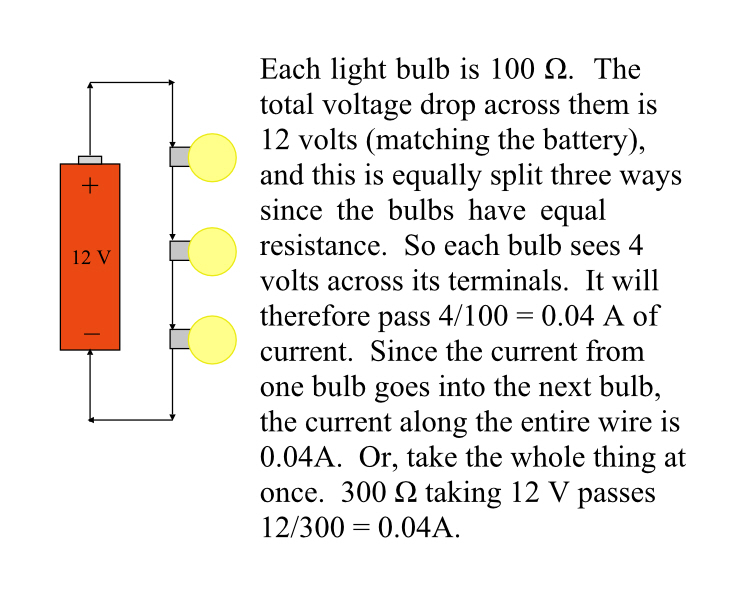
The current through any one of these lights will be 4V/100 ohms, or 0.04A. The same current goes first through one light, then the second, then the last, so it’s a good thing all of those currents are the same (or current would be coming in from nowhere).
By the way, on diagrams like this, for educational purposes, the wires are assumed to have zero resistance. So the voltage drop from the battery to the top terminal of the bulbs is E=IR = 0.4A • 0Ω = 0V. Likewise the wire between the bulbs has zero voltage drop.
Stringing a load end to end like that is known as wiring in series and usually is a stupid way to do things. (If one bulb blows out the circuit is broken and none of them work. Also, adding more bulbs increases the total resistance, reducing the current, and the total amount of light is actually less.)
Connect each of the three bulbs directly to the battery at both ends. This is parallel, because it splits the current into three separate streams. Each bulb now has 12 V across it, not 4, and the current through each bulb is 0.12A. Since each bulb gets a separate stream of current, the currents add up (instead of the voltages) and the battery is delivering 0.36A. Adding more bulbs adds more light, they each continue to use the same current as before.
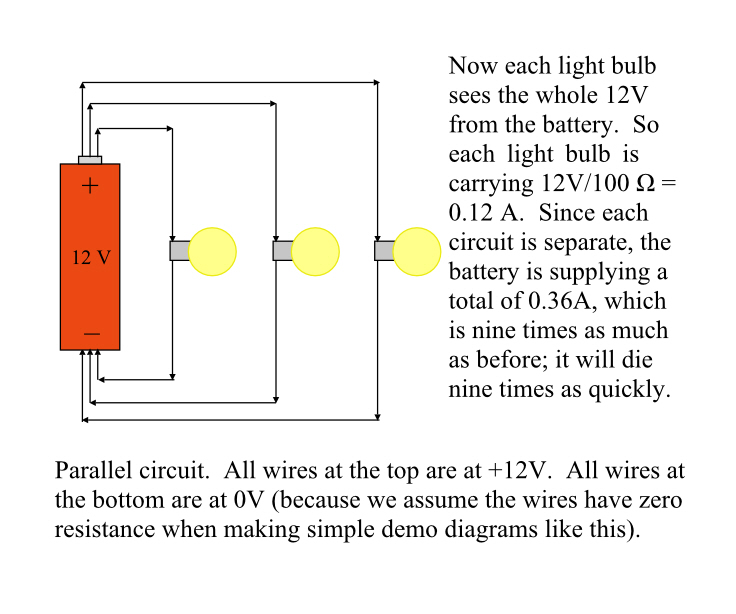
When wiring up a house, if there are, say, multiple lights controlled by one circuit, your electrician wired them in parallel, not in series. (Or he has made a rookie mistake.)
OK, one more thing, before we alas, must call it quits…prematurely.
Imagine a 1A current flowing. That’s one colomb/second (1 C/s). Imagine it’s flowing because of one volt of potential. A volt is 1 J/C.
What happens when you multiply current by potential?
C/s • J/C.
The coulombs cancel, and you’re left with J/s. Which is power, in watts. The same watts we had when we were playing with weights and forces.
(Incidentally, in the US, we tend to think of electrical things in watts–light bulbs especially. But with mechanical things, even an electric circular saw, we think of their power in horsepower. It’d be really odd for someone to brag about how many watts his car engine puts out, though he could. On the other hand, it’s perfectly normal in Europe though even they have a residual use of horsepower, judging at least from car marketing materials (though maybe that’s for the benefit of us Yanks). But just so you have a feel for the difference, one horsepower is 746 watts.)
But this shouldn’t be any surprise. Remember that a volt is what you needed to get a coulomb to do a joule’s worth of work. A current of 1 ampere means that a coulomb of electricity is having this done to it every second, in other words a joule of work is being done every second…which is a watt.
So P (for power) = I (for current…again, don’t ask me why) x E (for voltage).
We can now write many different equivalencies for the watt:
1W = 1J/s = 1V•A = 1 kg•m2/s2 = 1 V•C/s…
So we’ve figured out that electricity has potential, it has current, it has resistance and it has power, many of these analogous to gravity, many not really all that analogous at all.
Going back to those two diagrams above, the first has 0.04A flowing through a 12 V potential drop, that’s 0.48 W. The second has 0.36A flowing through a 12 V potential drop, for 4.32W. The latter circuit delivers nine times as much power as the former. Batteries are rated in A•h, not watt-hours, so what matters is how much current it delivers. Because it’s delivering nine times as much current (as well as nine times the power), that battery will die nine times faster.
Now going back to house breaker panels, we know the voltage (on average) is 120V. The breaker says it’s a 20A breaker. Multiply the two together, and the breaker carries 2,400 watts. Why not just label the breaker that way?
Because a breaker is designed to protect the circuit which has a limit on how much current it can carry. The circuit’s capacity is unaffected by the voltage of delivery but it had better not draw more than 20A. In fact the same breaker could conceivably be used in Europe, where the supply voltage is 220V, and therefore be able to pass 220V x 20A = 4,400 watts. (I don’t know if it’s physically compatible with the way their systems are laid out, though, so don’t go selling unused breakers to people in Europe to raise money when the Great Fiscal Apocalypse finally hits.)
There is much, much more to this story, we’re still in the early 1800s. I am sure Wolf will tell you I am quitting before the interesting part. And I am!
But I don’t want this to get overlong, and I still have to draw the diagrams, and it’s already 9PM in Wolf’s time zone.
I’m going to cover a totally different topic next week, then bounce back to this story the week after.
There is a mystery here, you might already see it, but it’s still a mystery in 1895, so let’s save it until we get there.
And Joe Biden didn’t win.
To Be Continued…
Obligatory PSAs and Reminders
China is Lower than Whale Shit
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!
