What is it that feeds our battle, yet starves our victory?

Do We Still Need the Kang (Mis)Quote?

I’m still using the quote about winning the battles but losing the war. It seems like this doesn’t make sense right now given that we seem to be going from triumph to triumph.

On the contrary. This is the exception that proves the rule. The quote isn’t just a lament, it’s to point out why we can never seem to win.

You see, the RINOs cannot interfere and that is why, just for once, we are actually winning. And that is just one more piece of evidence (for the willfully blind) as to what I have been saying with that quote.

It stays.

Speaker Johnson
Pinging you on January 6 Tapes

Just a friendly reminder Speaker Johnson. You’re doing some good things–or at least trying in the case of the budget–but this is the most important thing out there still hanging. One initial block released with the promise of more…and?

We have American patriots being held without bail and without trial, and the tapes almost certainly contain exculpatory evidence. (And if they don’t, and we’re all just yelling in an echo chamber over here, we need to know that too. And there’s only one way to know.)

Either we have a weaponized, corrupt government or we have a lot of internet charlatans. Let’s expose whatever it is. (I’m betting it’s the corrupt weaponized government, but if I am wrong, I’d like to see proof.)

Justice Must Be Done.

The 2020 election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Yes this is still true in spite of 2024. Fraud must be rooted out of our system and that hasn’t changed just because the fraud wasn’t enough to stop Trump winning a second term. Fraud WILL be ramped up as soon as we stop paying attention.

Otherwise, everything ends again in 2028. Or perhaps earlier if Trump is saddled with a Left/RINO congress in 2026, via fraud.

Small Government?

Many times conservatives (real and fake) speak of “small government” being the goal.

This sounds good, and mostly is good, but it misses the essential point. The important thing here isn’t the size, but rather the purpose, of government. We could have a cheap, small tyranny. After all our government spends most of its revenue on payments to individuals and foreign aid, neither of which is part of the tyrannical apparatus trying to keep us locked down and censored. What parts of the government would be necessary for a tyranny? It’d be a lot smaller than what we have now. We could shrink the government and nevertheless find it more tyrannical than it is today.

No, what we want is a limited government, limited not in size, but rather in scope. Limited, that is, in what it’s allowed to do. Under current circumstances, such a government would also be much smaller, but that’s a side effect. If we were in a World War II sort of war, an existential fight against nasty dictatorships on the brink of world conquest, that would be very expensive and would require a gargantuan government, but that would be what the government should be doing. That would be a large, but still limited government, since it’d be working to protect our rights.

World War II would have been the wrong time to squawk about “small government,” but it wasn’t (and never is) a bad time to demand limited government. Today would be a better time to ask for a small government–at least the job it should be doing is small today–but it misses the essential point; we want government to not do certain things. Many of those things we don’t want it doing are expensive but many of them are quite eminently doable by a smaller government than the one we have today. Small, but still exceeding proper limits.

So be careful what you ask for. You might get it and find you asked for the wrong thing.

Political Science In Summation

It’s really just a matter of people who can’t be happy unless they control others…versus those who want to be left alone. The oldest conflict within mankind. Government is necessary, but government attracts the assholes (a highly technical term for the control freaks).

His Truth?

Again we saw an instance of “It might be true for Billy, but it’s not true for Bob” logic this week.

I hear this often, and it’s usually harmless. As when it’s describing differing circumstances, not different facts. “Housing is unaffordable” can be true for one person, but not for another who makes ten times as much.

But sometimes the speaker means it literally. Something like 2+2=4 is asserted to be true for Billy but not for Bob. (And when it’s literal, it’s usually Bob saying it.) And in that sense, it’s nonsense, dangerous nonsense. There is ONE reality, and it exists independent of our desires and our perceptions. It would go on existing if we weren’t here. We exist in it. It does not exist in our heads. It’s not a personal construct, and it isn’t a social construct. If there were no society, reality would continue to be what it is, it wouldn’t vanish…which it would have to do, if it were a social construct.

Now what can change from person to person is the perception of reality. We see that all the time. And people will, of course, act on those perceptions. They will vote for Trump (or try to) if their perception is close to mine, and vote against Trump (and certainly succeed at doing so) if their perception is distant from mine (and therefore, if I do say so, wrong). I have heard people say “perception is reality” and usually, that’s what they’re trying to say–your perception of reality is, as far as you know, an accurate representation of reality, or you’d change it.

But I really wish they’d say it differently. And sometimes, to get back to Billy and Bob, the person who says they have different truths is really saying they have different perceptions of reality–different worldviews. I can’t argue with the latter. But I sure wish they’d say it better. That way I’d know that someone who blabbers about two different truths is delusional and not worth my time, at least not until he passes kindergarten-level metaphysics on his umpteenth attempt.

Lawyer Appeasement Section

OK now for the fine print.

This is the Q Tree Daily Thread. You know the drill. There’s no Political correctness, but civility is a requirement. There are Important Guidelines,  here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.

(Hmm a few extras seem to have crept in.)

(Paper) Spot Prices

Kitco “Ask” prices. Last week:

Gold $2,911.50
Silver $32.60
Platinum $974.00
Palladium $934.00
Rhodium $6,000.00
FRNSI* 139.844-
Gold:Silver 89.310-

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $2,985.50
Silver $33.87
Platinum $1004.00
Palladium $988.00
Rhodium $5,700.00
FRNSI* 143.424-
Gold:Silver 88.146-

Gold blooped up over the 3000 dollar mark briefly Friday, but retreated a bit and closed at the level shown above (it actually closed a bit higher than that on Thursday). So of course the FRNSI is at an all-time weekly high. Silver did very well this last week; long overdue; gold is now worth over an ounce less silver than last week. Platinum shows some signs of life. Maybe it is only mostly dead.

*The SteveInCO Federal Reserve Note Suckage Index (FRNSI) is a measure of how much the dollar has inflated. It’s the ratio of the current price of gold, to the number of dollars an ounce of fine gold made up when the dollar was defined as 25.8 grains of 0.900 gold. That worked out to an ounce being $20.67+71/387 of a cent. (Note gold wasn’t worth this much back then, thus much gold was $20.67 71/387ths. It’s a subtle distinction. One ounce of gold wasn’t worth $20.67 back then, it was $20.67.) Once this ratio is computed, 1 is subtracted from it so that the number is zero when the dollar is at its proper value, indicating zero suckage.

The Ides of March

Yes, our calendar is a direct descendant of the Roman calendar, particularly after Julius Caesar’s reforms.

That doesn’t mean we’d have any idea WTF we were looking at when looking at a Roman Calendar. They didn’t lay out months in tidy little rectangles like we do, with days numbered from 1-31. (Or 30, or 28 or fairly rarely 29.)

Nope they did something totally wacky, at least from our point of view.

The Kalends was the first day of the month. The Nones was the ninth day before the Ides. The Ides were, in turn the 15th day of full months (months of 31 days), or the 13th day of hollow months (months of 30 days) [Before Julius and Augustus Caesar, February had 30 days.] After some reforms months could have four different lengths and even the 31 day months were handled two different ways.

Counting through the days of the month, the 1st was “on the Kalends”. the 2nd was “the day after the Kalends” OR it could be called (in March, May, July and October–MMJO) the “Sixth day before the Nones” and for every other month the “Fourth day before the Nones”. Then count down each subsequent day until on the 7th (MMJO) or 5th (all others), was “On the Nones.” But beware because the “Third day before the Nones” was followed by “the day before the Nones” (there was no “second day before the Nones). The next day (8th or 6th) was “The day after the Nones.” OR that day could be called the 8th day before the Ides. Then the 7th, 6th, 5th, 4th, 3rd days before the Nones…and then skipping over “the second day before the Ides” to “the day before the Ides.” Then the Ides…which was on the 15th (MMJO) or 13th (all other months).

Then it gets tricky. For MMJO, the day after the Ides (the 16th) could be called “The day after the ides” or “the 17th day before the Kalends” Note, though that (for example) March 16 was called “the 14th day before the Kalends of April.” So April was being named…even though it was really still March! For January, August, and December, the “day after the Ides” (the 14th) was also “the 19th day before the Kalends”. For April, June, September, and November (all 30 days at the time), the “Day after the Ides” (the 14th) was “the 18th day before the Kalends”. For February (28 or 29 days) the “Day after the Ides” (the 14th) was either the 16th or 17th day before the Kalends of March”.

You would then count down to the second-to-last-day of the month and that would be the 3rd day of the Kalends, and the last day would be “the day before the kalends.”

Of course they did this in Latin, not English, so for example, they’d say “ante diem tertium decimum Kalendas” (the 13th day before the Kalends) and write it down as “a.d. XIII Kal.” since who wants to write all that out?

The day after Kalends, Nones, or Ides were considered “black” days and unlucky. (Though they were off one day for Julius Caesar.)

[Note before the Julian reforms, there were no thirty day months; there were MMJO (31 days), February (28 days) and everything else (29 days) and they followed the rules for MMJO, 28 day Februaries, and the 29 day February, respectively). When the caesars made January, August and December into 31 day months, they actually left the Ides in the same place relative to the Kalends (i.e., on what we call the 13th of the month) rather than moving the Ides to the 15th, to avoid messing up festival days.]

Somehow, they were able to use this insanely complex system and still have enough brainpower left to conquer the entire Mediterranean world.

And NO I don’t have this memorized, I had to look it up. https://en.wikipedia.org/wiki/Roman_calendar. Otherwise I’d not have the brainpower left to butcher the topic of geology.

A Deeper Dive on Isotopes

Last time I described the atomic nucleus as it came to be known during the early 20th century, and I discussed radioactivity. I touched on isotopes a bit; time for a deeper dive.

As chemists worked to measure atomic weights for all known elements (painstaking and unglamorous work; the ones doing this are the unsung heroes of chemistry) it became apparent that most elements had atomic weights that were almost an integer multiple of the element with the lightest atomic weight: hydrogen (for example, taking hydrogen as 1 (not the currently used value!), helium comes in at 3.971, very close to 4. But there were a few oddballs, too, elements with a not-very-close multiple, like (and now I’ll use the current values, with hydrogen at 1.008, not 1.000) boron (10.81), neon (20.18), chlorine (35.45). Just eyeballing the list it looks like about a quarter of all elements are “off” like this.

It wasn’t until people started ionizing elements and sending the ions through a magnetic field to see how much their trajectories bent that we started to understand this. This was first done by J. J. Thomson (who had discovered the electron, and loved to play with magnets and charged particles) in 1912 with neon gas. Neon is atomic number 10, ten protons, and as I mentioned its atomic weight is 20.18. Thomson discovered that neon is actually mixture of two different things, one with an atomic weight of 20, another with an atomic weight of 22. The signal was weaker for 22, so he figured it neon was mostly the atomic-weight-twenty stuff.

These were both undeniably neon; there was no way to separate them chemically because they both behaved the same (which is to say, being totally unwilling to engage in chemical reactions; neon is a noble gas). They just weighed different. Thomson however had been brought up believing that atomic weight was an inherent property of an element, so he thought of it as two separate gases. We don’t think this any more. They’re both neon. And we now know there’s a very small amount of neon atoms with a mass of 21.

As more and more of these experiments happened, it became clear; if an element’s atomic weight was far off from an integer, it was a mix of these “isotopes.” Aston (who formulated the “whole number rule” for isotopic masses) showed in 1920 that chlorine’s 35.45 atomic weight was due to being a mixture of atoms with mass 35 and mass 37 units.

When talking about just the nucleus of an atom, we often use the term nuclide instead of isotope (which is the whole atom). It’s not a hard and fast rule but chemists will tend to use “isotope” and nuclear physicists including those researching fusion will be a bit more likely to say “nuclide.”

Again, the chemical behavior is nearly identical. In principle a heavier isotope should be slightly slower to react than an lighter one, but the practical difference is nil except in one case. Thus when it matters (and it usually doesn’t), chemists and physicists will write something like neon-20 or neon-22. When they can do so they will follow the formal convention: ²⁰Ne or ²²Ne. I am able to do that here (writing the post) but not in comments; but it’s such a pain to do so (wordpiss), that I will stick with writing either neon-20 or Ne-20.

And by the way, for our purposes here, it does matter. Quite a lot.

The one exception regarding chemical differences is the case of hydrogen, which usually has mass number of 1, but some few atoms have a mass number of 2. If you concentrate the mass-2 stuff, and use it to make water, you have heavy water, which even though it’s technically hydrogen monoxide just like tap water is, will kill you. (It also melts at 4 degrees Celsius so it’s possible to put a heavy water ice cube in a glass of water at 1 degree Celsius and it won’t melt. It will sink to the bottom, too, which is even weirder.) In fact for hydrogen and hydrogen alone, there are “special” names for the heavier isotopes; hydrogen-2 is called deuterium and (in this context) hydrogen-1 is called protium. There is also hydrogen-3, which is radioactive and is called tritium.

Once the neutron was discovered by James Chadwick in 1932, we got some clarity as to what was going on. Neutrons, it turns out are very slightly more massive than protons, We now know that neon-20, neon-21 and neon-22 all contain ten protons (neon has ten protons, by definition), but they contain 10, 11, and 12 neutrons, respectively, the total of the two numbers 10+10, 10+11, 10+12 gives you the mass number.

So what happens when you do this sort of analysis on other elements as found in nature? Fluorine (#9) has one isotope, F-19. Tin (#50) has no less than ten isotopes: Sn-112, 114, 115, 116, 117, 118, 119, 120, 122, and 124. The natural proportion for each of these ranges from 0.34 percent to 33 percent.

It is possible to create isotopes in the lab. So long as the number of neutrons isn’t too high or low, you’ll get a nucleus that hangs together for a while, perhaps even permanently. Otherwise the excess neutrons will “drip” off (fail to stick even momentarily) or if there are too few neutrons, a proton will “drip” off.

Between these bounds, the isotope will be intensely radioactive, less intensely radioactive, even less intensely radioactive, dang near stable, or actually stable. (Those are not “official” terms by the way.) And if you include all those made-in-a-lab-and-very-unstable isotopes the isotope counts go way up. Tritium is one of them for instance, and tin actually has isotopes ranging from 99 through 140.

Why do we need to make those highly radioactive isotopes in a lab? Because if there were any on earth originally, they have long since decayed away and none are left.

[If you poke around on wikipedia you may see references to something being “observationally stable.” That means an isotope that they believe on theoretical grounds is almost stable but it’s so close to stable they haven’t caught it decaying yet. In other words “we think this ought to be very very mildly radioactive–so mild we haven’t detected it yet so maybe it’s really stable after all.” Three of the ten tin isotopes I mentioned are “observationally stable”]

Because we are able to produce almost-arbitrary nuclides in the lab, we have pretty complete tables of nuclides–both a table with columns and a bunch of numbers in them, like you see here: https://en.wikipedia.org/wiki/Isotopes_of_tin, or nice graphical ones like this:

You can click on this to make it larger, but even there you can’t see what’s written in the boxes. Here is a link to a version that is 17,800 pixels across: https://upload.wikimedia.org/wikipedia/commons/9/9d/NuclideMap.svg

Going across the bottom, you have the number of neutrons, going up you have the number of protons, as shown in this excerpt from the very lower left corner. Note that the same isotope number for different elements lie on a diagonal. (They also threw in a bare neutron, mass number 1, element zero.)

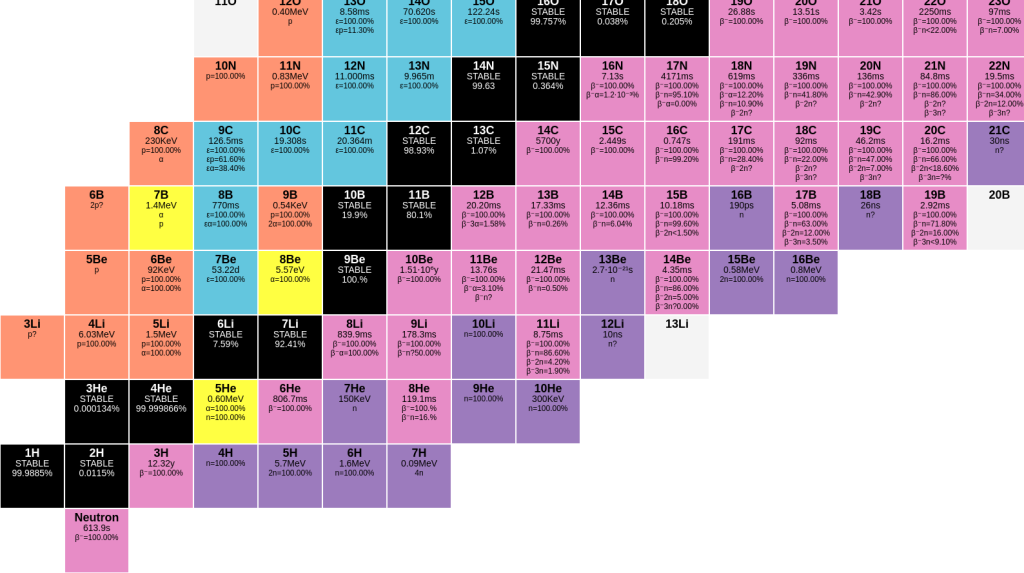
The colors indicate how the isotopes decay; black is a stable isotope. Blue is a β⁺ (positron) decay (or capturing an electron), orange is losing a proton (technically it’s “dripping” the proton), deep purple is dripping a neutron, yellow is alpha decay (note that ⁸Be alpha decays–and what’s left over is a helium nucleus, which is itself an alpha particle; so really it just splits in two). Green (visible at the other end of the chart) is spontaneous fission where a nucleus splits into two or more large pieces. Finally the pink or light purple squares like ³H are β^– (ordinary beta decay).

If you paid attention last time, you should be able to figure out what the isotope will turn into. For example ¹⁰Be undergoes beta decay, so it goes up one in charge (it now has 5 protons) but stays the same mass. It becomes boron-10, which is stable.

This chart also indicates half life. And I will more than likely be pasting in other pieces of it in future posts.

OK, so we have this list of all possible isotopes (and ones that arguably shouldn’t be considered isotopes because they “drip” when you try to create them). What do we see when we look “out there” on Earth? This is, after all, supposedly a series on geology, right?

The isotopes we see fall into three broad categories.

Stable isotopes. Every single stable isotope is found on Earth. Every last one.

Long lived isotopes. Isotopes over a certain half-life (which I will discuss below) will be found on Earth too. Again, every last one. (And by the way some of those half lives exceed present day estimates of the age of the earth by millions or even billions of times. And “observationally stable” isotopes, if they turn out to be radioactive, will have even longer half lives.)

Short lived isotopes. Some of the known short-lived isotopes can be found in nature. Here’s the thing though. In all of these cases, we can identify a natural process that is creating those isotopes, even at the present moment. For example, carbon-14 with a half life of about 5,760 years is being produced in the upper atmosphere by cosmic rays impacting nitrogen-14 nuclei. Uranium-234 has a half life of 245,500 years, and is created by uranium-238 decay (U-238 becomes thorium-234 due to an alpha decay, then Th-234 becomes protactinium-234 via beta decay, then Pa-234 becomes U-234 after another beta decay). All of those intermediate products, of course, we also detect in nature (and they have very short half lives of days or hours) so they fall into this category too. But, very important: We do not have any short lived isotopes we cannot account for this way.

This actually paints a picture: We have a situation where we have primordial isotopes–ones that apparently were always here on Earth, and the others, that weren’t. Since anything that could be a primordial nuclide based on being stable or having a long half life, is here, there’s no reason to suppose that some other nuclide that is now not found in nature wasn’t actually once here–only to have decayed completely away. Which means the Earth would have to be old enough for them to be gone by now.

OK, so what’s the dividing line between short lived and long lived isotopes? Somewhere between 100 and 700 million years.

I found this table: https://sites.astro.caltech.edu/~dperley/public/isotopetable.html which bills itself as all radio isotopes with half lives over 1000 years. I am going to excerpt everything between 1 million and one trillion years, below: