Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot (i.e., paper) Prices
Last week:
Gold $1880.70
Silver $27.63
Platinum $1172.00
Palladium $2834.00
Rhodium $25,500.00
This week, 3PM Mountain Time, markets have closed for the weekend.
Gold $1904.50
Silver $28.03
Platinum $1187.00
Palladium $2878.00
Rhodium $24,400.00
Unfortunately, when looking at the prices only on Friday, you lose some things. Rhodium took a hard hit during the week, dropping below $20,000. At least, according to Kitco. A different site I sometimes check never noticed that drop, so when rhodium came right back up again the downward plunge disappeared, for them. Gold definitely seems to be on an uptrend, and perhaps silver is too. Rhodium is off its all time high, but I am waiting to see if it will truly start to go down.
Torque and Angular Momentum (Part V of a Long Series)
Introduction
Having run out of precious metals to babble about, I’m going to change tacks. If you’ve been here a while, you might remember two postings I did on stars. These were independent posts, having nothing to do with politics (poly = many, ticks = blood sucking bugs) and at least some people enjoyed them. I wanted to go to the opposite end of the scale and talk about a certain sub-atomic particle, but then I realized that the best way to do that would be a very, very, very long post. (And yes, it’s a subatomic particle, but it has a lot to do with stars.) A huge part of it would be explaining where physics stood in 1895, and how three discoveries in the next four years basically overturned things, and eventually led to that subatomic particle, the real star (ahem) of the whole series.
So I decided to break this story up into pieces. And this is the fifth of those pieces.
And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it…but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)
Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I use 9.8, below, for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.
Dimensions and Units
I have another go-back.
I’ve been re-educating myself on a lot of this stuff, and I find I’ve been glossing over some critical distinctions.
In particular I’ve been sloppy about the one between dimensions and units. I may very well have never misused the one word to refer to the other thing, but even if not, I haven’t clearly drawn the distinction, and it may have led to some confusion (or at least the sense that I am switching my terminology without any particular reason).
To try to make it clear, let’s take as an example something that, though we’ve not covered it here, is something quite visual. Area. We all know about the area of a room in a house, and we typically measure it in “square feet” which is to say, how many squares a foot on a side will fit into the area. (If it’s irregular, or has fractional measurements, obviously we can cut up our squares into pieces to fit them in.)
The units of area here are in square feet, or feet•feet or ft2. But an area could just as easily be measured in square inches, or square yards, or square centimeters, or square meters. There is also the acre (which is 1/640th of a square mile), and the hectare (10,000 square meters or one square hectometer (100 meters on a side), roughly 2 1/2 acres). Those would all be different units for area. But the dimensions of area are length x length. Length is the thing a foot, or a meter, or a furlong, or a light year, actually measures, just as an acre measures area. When we go to talking about dimensions, we’ve divorced ourselves from any particular measuring system, and we’re talking in the abstract.
So, looking at work, in metric the unit of measurement is the joule, which is a newton-meter, which in turn is a kilogram-meter/second2 • meter, or abbreviating, kg•m2/s2. But the dimensions of work are mass•length2/time2, or abbreviating, m•d2/t2. (Unfortunately m can stand for the dimension mass, as well as the unit meter, adding to potential confusion.)
Physicists–and hard scientists in general, actually, engage in something called dimensional analysis from time to time. If they’re working on proving a relationship between two different things, the dimensions had better match up properly, or they’d know to go back to the begining and start again. For example, if Einstein, while writing that famous equation, E = mc2, had not had the dimensions match up, he’d have wadded up the paper he was writing on and started over.
But there’s also unit analysis. And chemists do this a lot because they have all sorts of specialized units of convenience (like the calorie) and often have to convert from one unit to another. Of course we do this all the time as well, just rather informally, but there’s a way to lay things out so they come out right and we don’t just have to guess.
Let’s say you own a large warehouse, 330 x 660 feet. You want to brag about how big it is because you want to sell it to someone. How many acres does it cover?
As I mentioned above a square mile is 640 acres. We also know that there are 1760 yards to the mile and three feet to the yard. (Pretend you don’t know anything else, in particular forget the number 5,280.)
So you can get the right answer, guaranteed, by doing something like this:
Write: 640ac/mi2, mi/1760yd, mi/1760yd, yd/3ft, yd/3ft, 330ft, 660ft.
The last two are the two numbers that go into your area, when you multiply them together you’re multiplying two lengths to get an area. So from a dimension analysis standpoint we’re good with those, but multiplying them together gives you 217,800 ft2 and we don’t know how to relate that to acres. So for now let’s not multiply them!
That’s where the rest of the crap I told you to write comes in. Look at each one. They’re all fractions equal to one. In the first case both top and bottom are equal to a square mile (or they’re both equal to 640 acres), so that first term is equal to 1. That’s true for the other four terms too.
So you can take your 330ft x 660ft and multiply it by all five of these and not change it, since they’re all equal to 1.
Let’s combine things.
640ac • mile • mile • yard • yard • 330ft • 660ft
——————————————————————————————
mile2•1760 yd • 1760 yd • 3ft • 3ft
The first thing you can do is cancel out the units. Feet, for instance, appears on the top twice, and on the bottom twice. Remove them all! The same with yards (twice on top and bottom). And mile shows up twice too, so remove them all.
Now you’re left with nothing but “acre” in the numerator, and a bunch of numbers.
640 acre • 330 • 660
——————————————-
1760 • 1760 • 3 • 3
This means when you do that arithmetic, you will have your answer in acres.
You can do some cancelling, you can divide the 330 and 660 by 3 and get 110 and 220. Then it turns out that 1760 is 16•110 (and therefore 8•220) so you can do some more canceling and get 640 acres / ( 16•8 ). This should be readily digestible as 5 acres.
This sort of procedure can be used to convert from metric to US customary, too, provided you know a conversion factor somewhere. For example, I know the metric system weights fairly well, and I also know something about the US customary system weights, but the only conversion factor I can remember is that 31.1035 grams makes up a troy ounce. I know for regular grocery ounces it’s 28-point-something but can never remember. So if I have 500 grams of something, how many grocery ounces does that weigh?
OK, working “backwards” from the desired answer to what we have, start with 16 oz / 1 lb. Then get there from grains, and get to grains from troy ounces, and get to troy ounces from grams:
(16oz/1lb)•(1lb/7000gr)•(480gr/1ozt)•(1ozt/31.1035g)•500g.
When you go through and cancel out all the units, you’re left with oz as the sole standing unit. You can then multiply and divide all those numbers and get that 500 grams weighs 17.63696+ grocery ounces. I only have to remember ONE conversion facter from US customary to metric, so long as I know the conversion factors within the US customary system. (The internal metric ones are much easier to remember!)
OK, that’s out of the way. On we go.
Torque
Up until now we’ve been working with forces that go entirely into making the object move from one place to another.
That’s because we’ve implicitly assumed the force was directed through the center of mass of the object.
However, you know, and have probably known since the first time you tried to push on an object as a baby, what happens when you don’t line up with the object’s center of mass: The object does some combination of turning and moving, and that motion isn’t in the direction you pushed!
Let us, for now, pretend we’re on a frictionless surface (or, perhaps, in orbit, freefall, which for complicated reasons is called “microgravity” by sticklers).
Figure 1A shows an object, and a vector representing a force applied to the object. The dot is the center of mass of the object. The force does not go through that center of mass.
Figure 1B shows the vector resolved into two components, a radial component (through the center of mass) and a transverse component, perpendicular to the radial component.
If your point of view is the center of mass, the transverse component is the one you see as a vector against the background. The radial component looks like a vector pointed right at you. (Figure 1C)
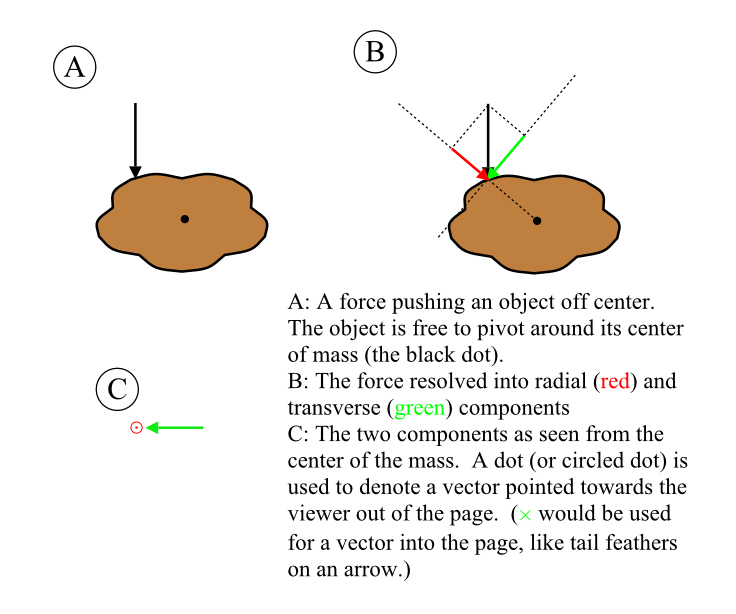
As it turns out the radial component goes into pushing the object, and the radial component’s direction, not the direction of the original force is the direction of the shove, the sort of shove we talked about way back in part 1 when we talked about mass and force.
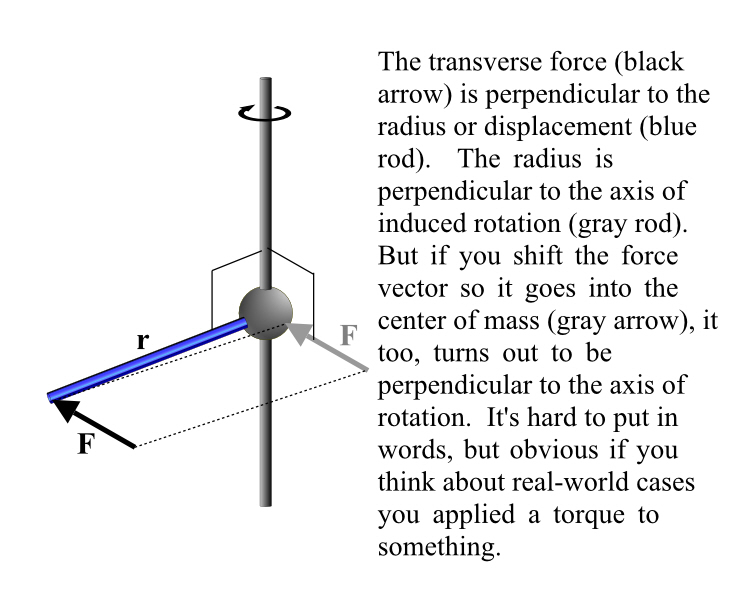
The transverse component will set the object to turning around its center of mass. (Or, if the object is fixed to a pivot, the object turns about the pivot.) This action is called torque.
Not only that, the induced rotation will be around an axis that’s perpendicular to the radial component of the force. And it will also be perpendicular to the transverse component. (That sounds complex, it really isn’t. It’s definitely one of those picture-equals-a-kiloword things. See Figure 2.)
Different objects will, depending on not just their mass, but also their shape (sphere, donut, cylinder, cube, flat sheet), orientation (it makes a difference whether a cylinder is oriented so the ends are on the axis of rotation, versus whether the axis passes through the “wall” of the cylinder), and mass distribution (is the mass uniformly distributed or is, say, most of it near the center of the object), resist the torque trying to get it to turn. These factors would be multiplied by the mass of the object to come up with something called the “moment of inertia.”
(If you see the word “moment” in a physics term, it has to do with getting something to rotate, either something like this, or, say, a magnet wanting to swing to point towards/away from a magnetic pole somewhere–that’s a magnetic moment.)
The moment of inertia of a point mass, m, at a distance r from the center of rotation (the pivot point), is mr2. You can determine the moment of inertia of actual, real shapes (not point masses) either around their own center of gravity or a pivot point elsewhere, by breaking the object up into infinitesimal (almost zero size) pieces, computing each piece’s moment of inertia, then adding them up again. This can be “automated” in large part by using calculus.
Note that moment of inertia seems to have dimensions mass • distance-squared.
For example, a solid, uniform sphere had a moment of inertia about its center of I = 2/5mr2, m being the mass of the sphere and r being its radius. And of course the center of gravity is the center of the sphere. But if it’s a spherical shell (where the thickness of the shell is very small compared to the radius), it’s 2/3mr2. If it’s a thin rod of length L, spinning around a perpendicular line through the center, it’s 1/12mL2. And moment of inertia doesn’t just apply to objects completely free to move. If that rod is attached to a pivot at one end, like (say) the arm of a wrench, the moment of inertia is 1/3mL2—four times as much.
Tedious stuff and I had to memorize it then (of course) forget it.
OK, here’s an application. You’re driving down the road and have a blowout. You now have the task of loosening the lug nuts on the wheel so you can change to the spare. Out comes the lug wrench, and you push on it to loosen the nut.
The handle of the wrench is a radial (displacement) vector, and you know, intuitively, that you get the most leverage if you push on it at a right angle, as far out as possible. You’re trying to loosen the nut which not only has a (very small!) moment of inertia but a lot of friction.
If it doesn’t want to come loose, you need more torque. There are two ways to increase the torque: Apply more force to the end of the wrench (making sure it’s perpendicular), or get a longer wrench.
By now you’ll have noticed a pattern. Any time doubling some piece of the puzzle doubles the effect, the formula is going to involve multiplying by that factor. In this case this happens to both the the force and the distance (length of the wrench). We use the Greek letter tau, τ, to denote the torque. Then, if Ft is the transverse component of the force:
τ = Ftl
So you can imagine applying three newtons of force to the end of a two meter wrench (if you can imagine a wrench that long!) or twelve newtons to the end of a half meter wrench, and getting exactly the same torque either way.
Note this isn’t a vector…but really, it should be! Torque absolutely has direction! Not only righty-tighty, lefty-loosey, but you’d never try to remove the lug nut by pushing toward the car or away from it, even though that’s also perpendicular to the wrench. You’re applying a torque by doing this, but it’s not in a useful direction. (In fact if you manage to bend or snap the lug, it’s worse than useless.)
So we have two obvious vectors, a displacement (length) vector, and the direction of the force. We also know from our personal experience that a perpendicular force exerts the most torque because the entire force is transverse. Other angles exert less.
So our vector formula should depend on the angle between the vectors.
Well, we have the dot product. Is that what we want?
No, it’s not. First, the dot product does not give you a vector…and torque absolutely has direction, not just amount (magnitude).
But the second shortcoming is worse. A dot product is zero when the two vectors are perpendicular, and is maximized when the vectors are parallel (and minus that same maximum when the vectors point in exactly opposite directions). That’s the exact opposite of what we want.
The Cross Product
So pardon me for just a few seconds while I bust out in those peals of evil laughter once again. Bwahahahaha!!!
We need the other way to multiply vectors. We need the cross product.
The cross product, represented with ×, is maximized for perpendicular vectors, is zero when the vectors are parallel (or point in opposite directions) and gives you a vector answer. Perfect! It behaves exactly like torque with force vectors in various directions.
And now you know why the dot product is always written with a dot, never a “multiplication sign” like you saw in elementary school. Because when it comes to vectors, those two symbols do not mean the same thing.
First the pictorial description. Then the trig. Then how to compute it given some vectors.
First, a cross product only exists in 3D space. It won’t show up in the Donald Trump 64D Chess Open Championship. Nor will it show up in your 2D diagrams, unless you’re really showing a slice of 3D space, in which case it still won’t show up in your diagram because it will point straight up out of the diagram (or into it).
The result of a cross product between A and B, A×B, will be a vector that is perpendicular to both A and B. To visualize this, make a fat L with your right hand (your right hand, not your left hand), with the thumb sticking out from the hand at a 90 degree angle. Now point the fingers along vector A. Now bend the fingers in the direction of vector B. (Hopefully you don’t have to contort yourself too much for this part. Figure 3 is safe, as long as you follow directions and use your right hand.) Your thumb points in the direction of the cross product, so long as the angle you sweep through is less than 180 degrees. (And for that matter, more than zero–angles less than zero would bend your fingers backwards, anyways.) If it is more than that, the cross product points the opposite way.

This is called the right hand rule. You use your right hand to determine the direction of the cross product.
OK, now here’s a thing about cross products that will seem kind of odd. Do the same thing, only do B×A. Start with your fingers along B, turn your hand around so that you can sweep towards A. Now your thumb is pointed in the opposite direction from before.
Well, now, that’s odd! A×B actually is the opposite of B×A.
A×B = – B×A.
This GIF shows the cross product of two vectors in an animation, it pauses at 0, 90, 180, and 270 degrees but watch the cross product vector grow or shrink when it sweeps through the other angles.

Now for the trigonometric interpretation. The magnitude of the cross product AxB is equal to the sine of the angle between them, times the magnitude of both vectors.
∥A×B∥ = ∥A∥ ∥B∥ sinθ
If A and B are unit vectors, it reduces to just plain sinθ.
Here, if you look at the angle from B to A as the opposite of angle from A to B, you can see why AxB = –BxA, because the sine of a negative angle is the same as the sine of the positive angle—except for a minus sign.
OK, now, if you’re dealing with two “raw” vectors, triplets of numbers, how do you compute their cross product?
It’s quite a bit more complicated than a dot product. However, there are a number of gimmicks to help you remember, and I’ll share my personal favorite.
Let’s take the vectors A = [2,7,3] and B = [5, 4, 6]. Let’s also take three vectors, i, j, and k. These three vectors are a physicist’s best friends, they’re unit vectors along the X, Y and Z axes. In other words, i = [1, 0, 0], j = [0, 1, 0], and k = [0, 0, 1]. (Note: I know I should put hats on them…but those characters are unavailable, so I’m settling for just using lowercase to denote a unit vector.)
Arrange things like this:
i j k
2 7 3
5 4 6
In other words, our unit vector friends, then vector A, then vector B.
Now repeat the first two columns:
i j k i j
2 7 3 2 7
5 4 6 5 4
Now start with the first i and run down and to the right, multiplying: i•7•6, which is to say 42i. This is a vector of length 42 along the X axis.
Do the same for j and k, you should get 15j and 8k.
Add these together, and get 42i + 15j + 8k. But, if you think of it, that’s just the vector [42, 15, 8], isn’t it? OK, save that off, we have to go on to the next step.
Start with k. Run down and to the left and multiply. k•7•5 = 35k. Move to the second i and do the same thing, then the final j. You should get 12i and 12j. You can add these up and get 12i + 12j + 35k. But that’s just [12,12,35], right?
OK, last step. Take the second vector and subtract it from the first:
[42, 15, 8] – [12, 12, 35] = [30, 3, -27]
Now I can say that (unless I made a boo-boo), [30, 3, -27] is perpendicular to both [2, 7, 3] and [5, 4, 6]. Which also means it’s perpendicular to the plane those two vectors are in (two vectors that aren’t parallel or antiparallel define a plane, but if the two vectors are like that then the cross product is zero).
Of course I can check that statement, and so can you. I can dot [30, 3, -27] with each of those vectors, if they are perpendicular the dot product will be zero.
[2, 7, 3] • [30, 3, -27] = 60 + 21 – 81 = 0
and
[5, 4, 6 ] • [30, 3, -27 ] = 150 + 12 – 162 = 0.
(So I guess I didn’t make a boo-boo.)
OK, that’s a kind of lengthy process. If you don’t like that, please, just remember the right hand rule and remember the gif. Those will tell you the direction, and give you a qualitative understanding of what’s going on.
Torque as a Vector
Okay, with that out of the way, back to torque. It’s the cross product of the force and the displacement vector, r, from the center of mass to where the force is being applied.
τ = r × F
We no longer need to specify the transverse component of F, the cross-producting takes care of that.
Let’s re-use the picture from Figure 5-2 and show you the torque vector.
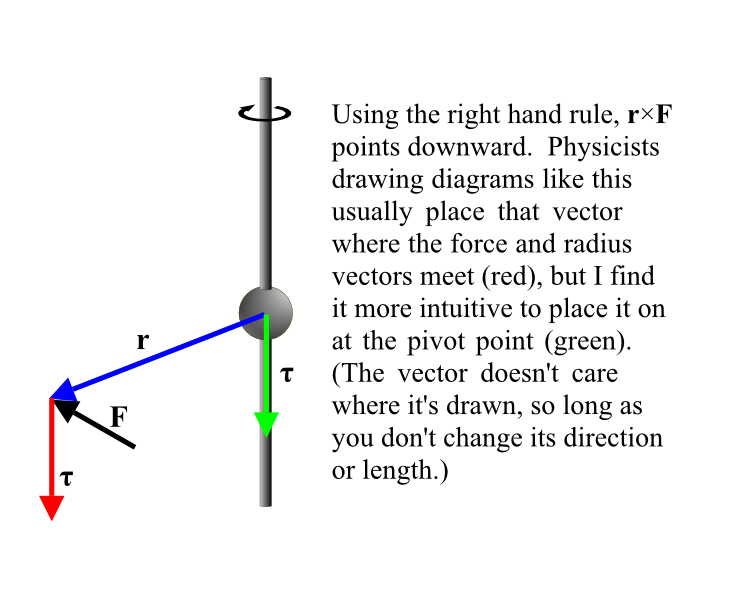
What about the units? F is a force and is in newtons, and r is a distance and is in meters. So torque is measured in newton-meters. Note this is the same units as work, but we don’t ever describe a torque in joules.
In the US customary system energy is sometimes measured in foot-pounds, and torque is quoted in pound-feet, just to keep them distinct.
And remember the direction of the torque is along the axis of rotation it’s trying to create. (In fact, it’s away from the car when loosening a lug nut, try the right hand rule to see.) If you find that counter-intuitive, you’re not alone. You might think the direction of torque ought to be the same direction as the force, or at least the transverse component of it. But on further reflection, that won’t work. In trying to loosen that rusted lug nut, I can be pushing down on a wrench sticking to the left, or I can be pulling up on the wrench while it sticks to the right. Those would be opposite torques if the direction of the torque were the same as the direction of the force. But they’re intuitively the same torque. If that isn’t so intuitive to you, then consider the case where you’re using one of those X shaped tire irons and you are pushing down on the left and pulling up on the right at the same time. The forces should cancel each other out, but clearly the torques they cause do not, they add together.
If you take both cross products left × down and right × up, both give you a vector pointing away from the car, and they add to each other.
Another way to look at is, the force, no matter where it is, is in a certain plane, the plane of the lug nuts. One way to specify a plane is to specify a line perpendicular to it. Of course, this is a vector, and can be anywhere so long as you don’t change its direction or magnitude, so a vector specifies any of a number of parallel planes (like pages in a closed book) depending on where you put it. A vector specifies a specific orientation of a plane, then,
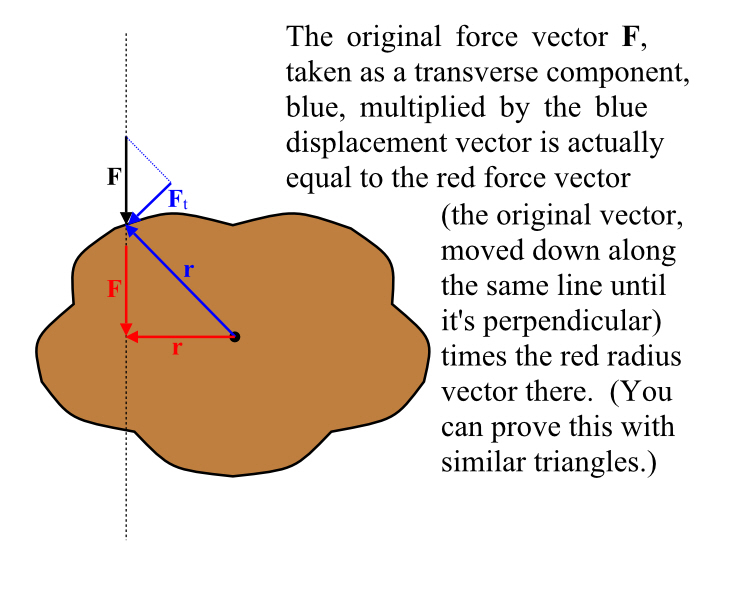
There is actually another way to analyze a torque when you are forced to push on the lever at an angle that isn’t perpendicular. Extend the line of the force, either forward or backward. Find the point where it’s closest to the center of rotation. Use the full force at that point and the distance to that point, and simply multiply (the angle is 90 degrees, so the sine factor is 1). This works because the length reduces by the same factor as you lost by not applying the force perpendicularly; you can prove that geometrically.
Angular Displacement, Velocity, and Acceleration
Imagine a wheel, free to turn, frictionless. You push on the outer rim. That’s a torque. How much does the wheel speed up?
As you might guess, it won’t turn at a high RPM immediately but will speed up as you continue to apply the torque.
You can actually draw a useful analogy here. We talked in Part I about applying a force to am object with a certain mass, causing it to speed up and, given a certain amount of time, covering a certain distance or displacement.
For rotations, we can apply a torque to an object with a certain moment of inertia, causing it to speed up in angular velocity (RPM is a measure of angular velocity) and eventually turn through a certain angle.
It’s actually a pretty tight analogy, everything “works.”
Distance (displacement) is represented by d. Angle, as you’ve already seen, is represented by lower case Greek theta, θ. But here’s the schiff in the punchbowl: the angle isn’t measured in degrees, it’s measured in radians.
A radian is 57.295779513082320876798 degrees.
Approximately.
Where the heck did that number come from? Okay, imagine you’re at a Biden rally, there to heckle, and you’re standing on the edge of one of those silly-ass social distancing circles. And the circle has a radius of 6 feet.
Now walk along the arc of the circle exactly six feet. The angle you covered is one radian. If you were to walk completely around the circle (why not? It’s not as if Biden is worth listening to) you’d cover 6 × 2π feet (approximately 37.699111843 feet), because the circumference of a circle is 2πr. That’s 2π radians. In other words, if you’ve expressed an angle in radians, you’re giving the ratio between the distance along the arc and the radius of the circle. And for reasons I long ago forgot (if I ever truly understood them) this is the most “natural” way to measure an angle, from a mathematical standpoint. (If you take a trig class you will learn like Pavlov’s dogs to recognize, for example, π/6 as being 30 degrees [with a sine of 0.5 and a cosine of 0.866+].)
Since an angle measured in radians is distance along the arc divided by the radius, you’re dividing length by length and a radian is actually a dimensionless value.
Velocity in a straight line is represented by v, the dimensions are distance/time Angular velocity, measured in radians per second, is represented by lower case Greek omega, ω. The units are 1/s, because the angle is dimensionless. Physicists usually write it as s-1, but I’ve avoided that so far and actually written fractions.
It’s possible to think of ω as a vector! It’s circular motion, though, so we cannot use the instantaneous regular velocity, just like we couldn’t define the torque vector as being in the same direction as the force producing the torque. You can define it as r × v or you can visualize it with a variation of the right hand rule. If the fingers of the right hand are curled in the direction of the circular motion, your thumb points in the direction of the vector. So if something is rotating counterclockwise (as seen by you), the angular velocity vector points towards you. [However, do not think of an angle as a vector; it doesn’t follow certain laws of vector addition. A long story…]
Mass is represented by m. Moment of inertia is represented by capital I: I.
Acceleration (in a line) is a. Angular acceleration is represented by lower case Greek letter α. And is in radians per second squared, i.e., 1/s2 or s-2.
And we’ve already seen F (linear force) and τ (torque).
You can follow through the analogy quite well. But I want to get to a specific destination, angular momentum.
But before we go there, if you’re really alert, you may have noticed one bit of the analogy doesn’t seem like the others.
Angular displacement, angular velocity, and angular acceleration are “sort of” like their linear counterparts, but in all cases, the displacement dimension disappears in the angular quantities.
But with torque, the displacement unit doesn’t disappear, it gets worse! Force is measured in newtons, kg m/s2. Torque is measured in newton-meters, kg m2/s2. There is a distance-squared in there, versus a distance, not the no-distance-at-all we’d expect from the analogy.
But in fact this is not a problem. A torque acts to accelerate an object with a moment of inertia at a certain angular acceleration. A torque, by analogy with F=ma, ought to be:
τ = Iα
I has units kg•m2 and α has dimensions 1/s2, combined they are kg m2/s2. This turns out to be newton-meters. So the analogy actually continues to hold, thanks to the fact that the mass-analog includes d2 in its dimensions.
And this is the case for momentum, and its analog, angular momentum as well.
Momentum is p = mv, yes, it’s a vector. Angular momentum is the same sort of thing, for a spinning object. It’s symbolized by L.
And you might expect angular momentum to be the mass-analog times the velocity analog. And indeed, it is:
L = Iω
This has dimension mass•distance2/time, md2/t or in MKS units, kg•m2/s.
You can rearrange this a tiny bit, and get L = md/t • d.
Notice, though, the first part of that has the same dimensions as momentum. And d of course is the distance.
It’s almost as if angular momentum is just regular momentum, times the distance from somewhere.
And indeed, the formal definition of angular momentum of a particle of mass m at a distance d from some point is:
L = r × p
It’s back!!! Here’s the cross product, again, and I could even just recycle some of my figures from earlier on by changing F to p and τ to L. In fact, what the heck, here’s figure five with the central mass removed.
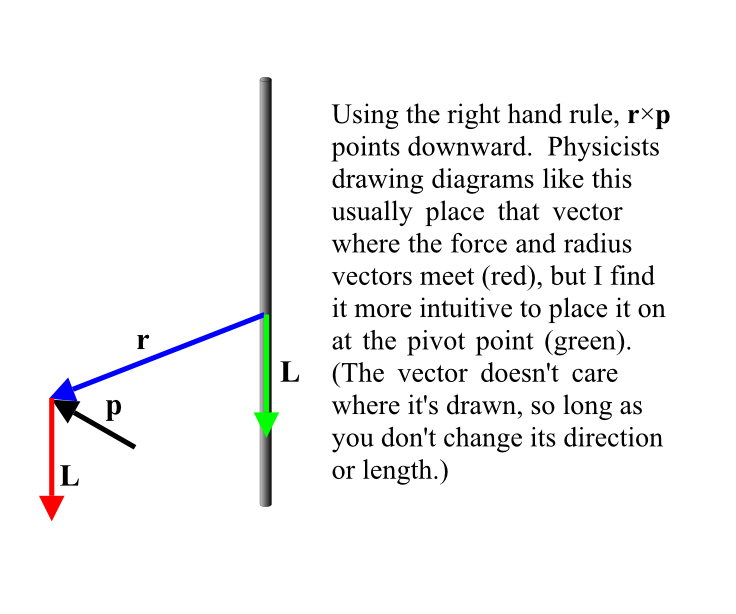
People have a tendency to think of angular momentum as having to do with spinning objects only, or maybe their outlook is a little broader and they’ll give an angular momentum to one object running in rings around another.
But actually, angular momentum applies to everything. If you’re standing by a highway, and a car goes whizzing past, then from your standpoint the car has angular momentum, even on a dead-straight highway!
That definition above doesn’t say a single solitary thing about angular velocity. It does have linear velocity built into p, however! And the car certainly has a lot of that and a lot of mass so p is huge.
When the car was a mile away, it was headed almost directly at you. The radial component was almost as big as its total speed, and there was almost no transverse component. As it drives by, it’s closer, but all of the motion is transverse. This should sound familiar.
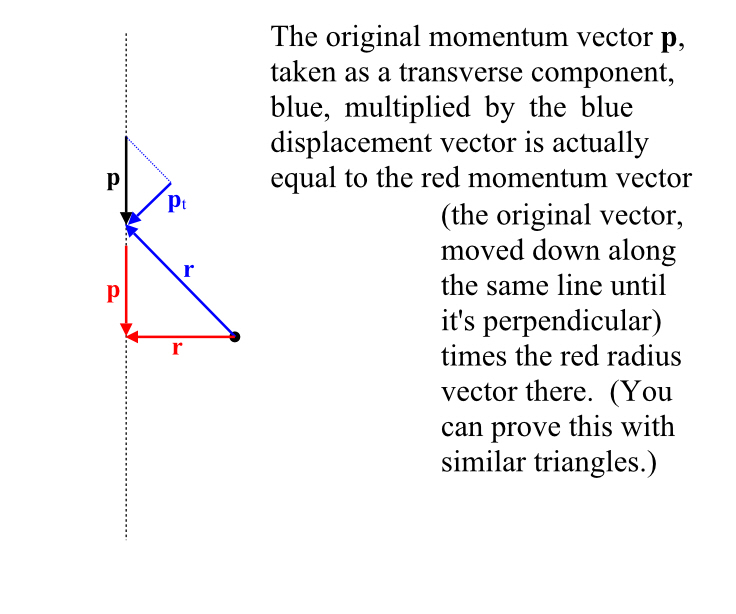
Here, I recycled figure 6, same substitutions. Instead of this being about the torque for a force applied anywhere on a straight line being the same, it’s the angular momentum that’s the same anywhere along a straight line, so long as the object is moving along with constant momentum.
I remember a story problem from a physics book (I cannot find it in my old college textbook, though). A child in a playground is running in a straight line, fixing to jump onto the edge of one of those rotating platforms that have probably been banned from playgrounds now because some idiot thinks they’re white heterosexual male. He has a constant angular momentum (seen from anywhere, but in particular the axis of the platform), then at the instant he jumps onto the platform, his motion is all transverse, and now that he’s revolving about the center of the platform, his motion will remain perfectly transverse. You can mentally relate angular momentum from rotation to angular momentum of an object moving in a straight line this way.
And, here is the freaky thing. You could pick any point on the diagram, and moving objects anywhere on the diagram would maintain the same angular momentum as they move along, relative to that point, as long as they don’t interfere with each other.
Conservation of Angular Momentum
You know, if momentum is conserved in a closed system, maybe angular momentum is also conserved. And indeed that turns out to be the case! Without exception, angular momentum in a closed system, relative to a point in that system, is conserved, and that includes objects in the system spinning about an axis. So even if objects interfere with each other by colliding, or whatever), the total angular momentum will remain the same.
The almost cliche illustration of the conservation of angular momentum is to watch a figure skater spin. When her arms are outstretched, she’s turning slowly, perhaps skating through a turn. Then she brings her arms in, raising them above her head, and suddenly she’s spinning, fast. Then she puts her arms out again and slows down. She’s reducing (and then increasing) the size of the displacement, so the rotation must increase (then decrease) so that the angular momentum will stay the same.
I also remember, but cannot find, a video of an astronaut on Skylab. He’s “standing” perfectly straight, perfectly still. His angular momentum is zero. He then kicks one leg forward, and one leg back, he then sweeps them around 90 degrees–which makes his body turn, but only while he is sweeping his feet around in arcs. Then he returns to standing. He’s managed to turn himself 90 degrees to the right, but he is again motionless. It’s a demo of the conservation of angular momentum because while his feet were moving in arcs, his body had to rotate in the opposite direction to keep his net angular momentum at zero.
And of course there is the gyroscope, but that one is complicated…and I’m going to skip it. Suffice it to say that the force pulling on the axis of the gyroscope is being crossed with the angular momentum vector (which is through the axis), and a vector in a totally different direction results. Optional homework, go find some youtube videos of gyroscopes and see what they have to say.
Applications
But now, let’s apply this to something a lot cooler than lug nuts and kids in a playground and an ice skater. How about an object in orbit around the Earth?
If it’s in a circular orbit, then it’s going to remain moving at the same speed and it’s a no-brainer, the angular momentum won’t change because neither the angular velocity nor the distance will change, and you don’t even need the vector form of the equation, because in a circle the two are at right angles, always. (Of course to verify that the direction doesn’t change, go ahead and take the cross product.)
But what about in an elliptical orbit? At one end of the ellipse, the satellite is closer than at the other end. At periapsis (closest point) and apoapsis (furthest point), furthermore, the motion at these two points is all transverse. So if angular momentum is conserved, the satellite must be moving slower at apoapsis than it does at periapsis. At any other place on the ellipse the satellite has some radial motion, it’s either climbing to its apoapsis or descending to periapsis. So those are harder to analyze.
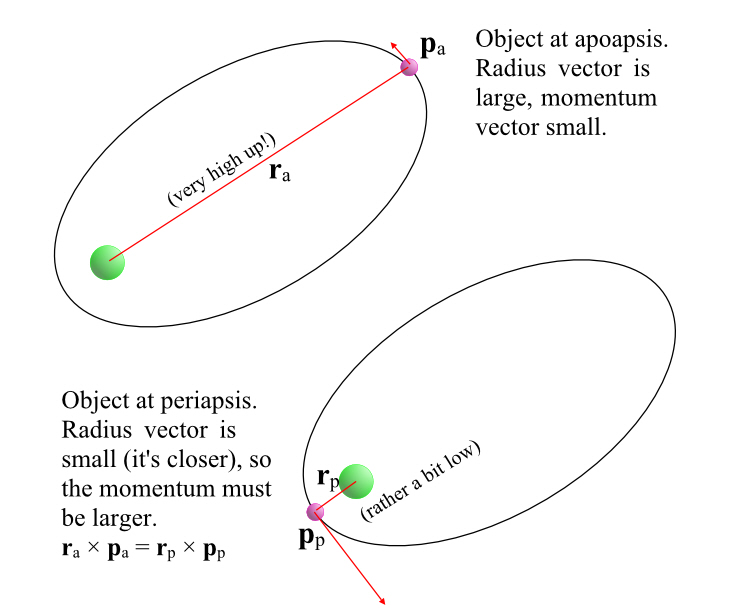
Kepler’s second law, put forward in the late 1500s (!) describes the motion of a satellite in an elliptical orbit. But it doesn’t just say the satellite slows down the higher it goes, it goes further. It says if you draw a line from the primary through the satellite, and look at the area it sweeps out in some time interval, it’s constant! A fat wedge when the satellite is close in, a skinny one when the satellite is further out.
I always wondered how the heck Kepler figured that out.
I’ve seen how it’s done today; you do some calculus on the r and p vectors after setting their cross product to a constant (because angular momentum is conserved) and it pops out, very readily, in less than five minutes of chalkboard time. (And I don’t remember exactly how, just that I was surprised how readily it occured.)
But that’s not how Kepler did it. He didn’t know about the conservation of momentum, and he didn’t know calculus. No one did at that time, because Newton wasn’t even a gleam in his father’s eye.
So I’m still wondering how Kepler did it.
Another cool application of what we learned today to the orbiting satellite, is that it’s very easy to compute the orbital inclination. The orbit is in a plane. The primary is on that plane too, it’s at one focus of the ellipse. But the plane could have any arbitrary tilt. Maybe it sits right over the equator, and maybe it’s at some tilt (like the tilted circle on a globe that’s supposed to represent the ecliptic somehow–I always thought those were silly because as soon as the Earth rotates a tiny bit, that line is wrong).
If you have a measurement of the satellite’s position at a certain point in time and its velocity (including the direction!) at that same time, and they’re vectors in the right coordinate system (one where x and y point at two places over the equator and z points through the north pole), you can take the cross product. Both of those vectors are in the plane of the satellite’s orbit. so the cross product is perpendicular to that plane.
You can then turn that cross product into a unit vector. Take the dot product of it and the k unit vector (usually taken as pointing through the earth’s axis. (Actually you can save yourself some time. Just grab the third element of the unit vector). That’s the cosine of an angle, take the arccosine to get the angle. You now have the angle between a line perpendicular to the plane of the orbit and the earth’s axis, which is the same as the angle between the plane of the orbit, and the earth’s equatorial plane. Easy peasy, doable with almost no data.
This Week’s Mystery
We have a conservation law. I usually try to come up with an 1895 mystery too. Well we have one.
Consider the solar system. 99.9 percent of the mass is in the Sun, which is about 800,000 miles across, and rotates in about 28 days. That’s a certain amount of angular momentum.
The other 0.1 percent of the mass is in the planets (with a small fraction of that small fraction in asteroids, comets, etc). They’re light weight compared to the sun, but they are far out there, and remember there is an r2 term in angular momentum. Mercury, the closest one out, is roughly 100 times as far out from the sun as the sun’s radius. Neptune is almost 100 times as far as that.
It turns out that the vast majority of the solar system’s angular momentum resides in the planets. The Sun is the “one percent” when it comes to mass, but the planets are the “one percent” when it comes to angular momentum.
The mystery is how that came about. And any theory of how the solar system was formed has to explain how the heck all the angular momentum ended up out there in the planets, because angular momentum is conserved. You can’t have the sun just shed angular momentum, it has to be transferred. So if your theory can’t explain that…it can’t explain Jack.
A number of different ideas were proposed as early as the late 1700s, perhaps the most prominent of them is called the nebular hypothesis. It suggests that the solar system formed from a shrinking nebula of dust and gas. The nebula, when initially all spread out, is going to have some very small net rotation (it’s a random melange of particles moving at random velocities, after all; the chance of them all cancelling out perfectly is close to zero). As the nebula shrinks it’s going to spin faster, a disk will end up being formed and the disk will be clumpy and the clumps will eventually form planets because the clumps will tend to attract more matter to them.
Fairly elegant, but it could not explain the distribution of angular momentum, so by the end of the 1800s it had fallen out of favor. I had a book on the planets as a kid (which was probably about ten years old when I was born) that still considered it a mystery, and contained some of the alternatives that had been proposed, including one that suggested the planets had been pulled out of the sun by another passing star’s gravity. (If that one is true, then solar systems ought to be rare, rare, rare.)
Just this once, I’ll give it away now. Unlike back then, today we can actually see some stars forming, and they are surrounded by disks of gas and dust, exactly like the nebular hypothesis. Some astronomers have done a lot of work to refine the nebular hypothesis to make it more detailed and try to address the angular momentum problem…but they still haven’t succeeded. Yet we now know it must be correct, because we can see it happening right now. So the answer to this one is, we still don’t really know. It’s conceivable (though not bloody likely) that the conservation of angular momentum is broken (even though it has been reliably true every. single. time. we have looked at it). More likely, there’s some process at work we don’t understand, perhaps even transfer via magnetic fields.
But we haven’t got to magnetic fields yet…
Obligatory PSAs and Reminders
China is Lower than Whale Shit
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

Three minutes to spare — hardly even exciting….
Yes, except that they start evacuating the center beginning at two minutes, to assist the atomic bomb….
imdb doesn’t have the quote (?), but it may have been “pumping the air out of the complex” instead of “evacuating the center” to avoid confusion with getting people out.
Anyone else remember this movie?
Good news.
I’m delighted to say that it seems as though the runt is about to get squashed like the vile little cockroach he is.
Happy Memorial Day weekend. 🇺🇸
https://theconservativetreehouse.com/2021/05/28/investigative-journalist-and-author-sharri-markson-reveals-how-dr-fauci-restarted-gain-of-function-research-after-obama-administration-stopped-it/
.

(PS – I don’t buy the “Obama stopped it” story one bit, which is not to say he didn’t, but rather that that was done in order to set Fauci up as the fall guy knowing all along they were going to use the scamdemic and might need a sacrificial lamb if things went sideways.)
Agreed. IMO Obama used the 2014 ban as a plausible reason to shift the research to China. Now there is need to protect Obama.
And the only reason there is a ‘need’ to protect the Hussein isn’t because anybody likes the Usurper, it’s because the Usurper is the buffer (or shield) between the light of day and Hussein’s handlers.
They’ll throw the crooked Kenyan under the Monster Bus lickety-split when the time comes, just like they’re preparing to do to Tiny Tony. 😁
Absolutely. Meat shields abound in their circles.
Tony the Tiny… 👹🎇👻
COVID protein spikes…. they’re gggggreeeeaaaatttt (ly deadly)…..
There’s always been a burden for protecting Zero way before this episode.
NATURE: Inside the Chinese lab poised to study world’s most dangerous pathogensMaximum-security biolab is part of plan to build network of BSL-4 facilities across China.
BY David Cyranoski
22 February 2017 Updated: 23 February 2017
If you do not think the Chinese IMMEDIATELY started to use that lab, I have a bridge to sell you…
ALSO
The University of North Carolina is a BSL-3 biowarfare lab NOT a bio level 4!!!
>>>>>>>>>>>
Dr Boyle, mentions this paper Published on November 8, 2015
“A SARS-like cluster of circulating bat coronaviruses shows potential for human emergence.”
It was Electronically
And LOOK who funded it! The National Institutes of Health under Fauci AND the State Key Program for Basic Research Grants from the Chinese Ministry of Science. Fauci not only funded the initial research but indicated interest in funding further research according to Dr Boyle.
SO…
TIMELINE:
1975 — Biological Weapons Convention
… was the first multilateral disarmament treaty banning the production of an entire category of weapons. It currently commits the 170 states which are party to it to prohibit the development, production, and stockpiling of biological and toxin weapons. However, the absence of any formal verification regime to monitor compliance has limited the effectiveness of the Convention. As of April 2013, an additional 10 states have signed the BWC but have yet to ratify the treaty.
https://military.wikia.org/wiki/Biological_Weapons_Convention
CHINA (1974) is a signatory as is the USA (1975).
1990 US Biological Weapons Anti-Terrorism Act of 1989
2010 — Dr Boyle mentions an Australian Gain-of-Function paper.
Published: June 22, 2010 Angiotensin-converting enzyme 2 (ACE2) proteins of different bat species confer variable susceptibility to SARS-CoV entry
End of 2014 – Wuhan Lab completed.
2015 – UNC paper, “A SARS-like cluster of circulating bat coronaviruses shows potential for human emergence.”
12 November 2015 — And just in case there is ANY doubt about what the UNC scientists were doing there is this article in Nature (the same guys who support Global Warming papers and refuse to print papers not supporting that conjecture.):
Engineered bat virus stirs debate over risky research (Update note from editors March 2020 denying lab made covid-19)
So it looks like they are busy covering up the Aussie/USA/China connections to this Gain-of-Function BIO-WEAPON
Bat Lady Bio:
Interesting papers/activities:
Ph.D, major in Virology, University Montpellier II, Montpellier, France.
07/01/2000 – Present Research Scientist in Wuhan Institute of Virology, Chinese Academy of Sciences, China. ,
02/22/2006 – 05/21/2006 Senior Scientist and Principal Investigator, Wuhan Institute of Virology, Chinese Academy of Sciences, China. ,
10/02/2006 – 10/23/2006, Visit scientist in Australian Animal Health Laboratory, CSIRO, Australia
01/01/2011-12/31/2015 Biosafety course training in BioMérieux P4 laboratory, France Grants (recent five years):
01/01/2013-12/31/2017 Mechanism of interspecies transmission of zoonotic viruses, National Basic Research program of China, project no: 2011CB504700. Co-Principal Investigator. 1,300,000 RMB.
01/01/2013-12/31/2017 Mechanism of interspecies transmission of zoonotic viruses, National Basic Research program of China, project no: 2011CB504700. Co-Principal Investigator. 1,300,000 RMB.
01/06/2014-31/05/2019 Identification, genetic evolution and pathogenesis of bat viruses in China. National Natural Science Foundation of China, project no: 81290341. Co-Principal Investigator. 2,900,000 RMB.
GOTCHA FAUCI!!!!
………..
𝟘𝟙/𝟙𝟘/𝟚𝟘𝟙𝟜-𝟛𝟘/𝟘𝟡/𝟚𝟘𝟙𝟡 𝕋𝕙𝕖 𝕖𝕔𝕠𝕝𝕠𝕘𝕪 𝕠𝕗 𝕓𝕒𝕥 𝕔𝕠𝕣𝕠𝕟𝕒𝕧𝕚𝕣𝕦𝕤𝕖𝕤 𝕒𝕟𝕕 𝕥𝕙𝕖 𝕣𝕚𝕤𝕜 𝕠𝕗 𝕗𝕦𝕥𝕦𝕣𝕖 𝕔𝕠𝕣𝕠𝕟𝕒𝕧𝕚𝕣𝕦𝕤 𝕖𝕞𝕖𝕣𝕘𝕖𝕟𝕔𝕖. ℕ𝕒𝕥𝕚𝕠𝕟𝕒𝕝 𝕀𝕟𝕤𝕥𝕚𝕥𝕦𝕥𝕖𝕤 𝕠𝕗 ℍ𝕖𝕒𝕝𝕥𝕙 ℕ𝕀𝔸𝕀𝔻 ℝ𝟘𝟙𝔸𝕀𝟙𝟙𝟘𝟡𝟞𝟜. 𝟞𝟞𝟝,𝟘𝟘𝟘 𝕌𝕊 𝕕𝕠𝕝𝕝𝕒𝕣𝕤.
………..
2014
Joint China-US Call for Employing a Transdisciplinary Approach to Emerging Infectious Diseases. EcoHealth, DOI: 10.1007/s10393-015-1060-1. 35. Hu, B., Chmura, A. A., Li, J., Zhu, G., Desmond, J. S., Zhang, Y., Zhang, W., Epstein, J. H., Daszak, P. & Shi, Z*.
The animal origin of SARS coronavirus; from genome to receptor usage. The 3rd annual “host pathogen interaction in biodefense and emerging infectious diseases” conference. Feb. 12, Manassas, Virginia. YANG X and SHI, Z et al.
….
I think you get the picture
https://www.ws-virology.org/wp-content/uploads/2017/11/CV_SHI-ZL-2018_ASM.pdf
Does anyone remember that we went to war because of possible bio weapon in in Iraq? They did not find any. Was that a putting an idea into our head? Was that an excuse for us to start research on creating bio weapon?
How long has this bio weapon idea floating around?
I thought there was a mutural ban on bio weapons?
I am just trying to connect some dots. They might not be there .
Sing, yes there was a ban and the USA and China signed it!
1975 — Biological Weapons Convention
That is the problem they stop just when it counts.
“(PS – I don’t buy the “Obama stopped it” story one bit, which is not to say he didn’t, but rather that that was done in order to set Fauci up as the fall guy knowing all along they were going to use the scamdemic and might need a sacrificial lamb if things went sideways.)”
___________
Political Moonshine has documented Obama inserting ‘pandemic preparedness’ into the Presidential Transition process, so Hussein is directly implicated. So (some of) his crimes against humanity have already been revealed.
The Hitler mustache belongs on the Kenyan Usurper and his brood of vipers even more than it belongs on Tiny Tony Mengele.
I agree that little Tony was set up to be the fall guy, but there seems to be more to the story.
The other side took preventative measures against being stopped by Trump. And then they moved up the time table for the release to pin the blame on the Lion rather than the donkeys.
Diabolical.
Yeah, that’s a pretty hard graph to ignore.
Bottom line – we were pushed into bad vaccines to advance gentech. TREATMENT with old drugs instead would have saved a lot of lives.
The most chilling moment, to me, was when the French Ministry of Health (or whatever its name is) abruptly yanked HCQ off the OTC medications list and out of pharmacies and drug stores…..despite it having been OTC for 60 years….and despite French citizens still regularly traveling to/from former colonies prone to malaria.
That’s when it became obvious that people were going to be killed and the killers didn’t care, and the conspiracy was worldwide.
See also https://www.zerohedge.com/covid-19/ivermectin-new-penicillin
Yeah, that was brutal. These people are Stalinists. They do the “Barr water bottle shrug” about “some people are going to have to die to fulfill our goals of fewer people which we think is good but we’re not sure but that’s OK because we’re running things and you’re not”.
I have thought a lot about that “Barr shrug.”
I never said a word about it, because at the time it was so pleasing to people because it looked like he was on OUR side. BUT.
That shrug and attitude were a bit disturbing. It looked like extreme arrogance and imperiousness to me. People like that are so confident in their essential “correctness” that they do whatever THEY think is right, without regard to others opinions. That can be dangerous.
I wanted to like and trust Barr, so I ignored the “pings.” I won’t do it again.
There seems to be a pretty good rule for detecting swamp rats.
Anyone with an official position who has spent his entire life not being Donald Trump.
AMEN.
Macaroon is owned by the deep state. Like all good French politicos, he went to “all the right schools” and did all the right things. And, that he could fool around and then marry his “momma wife” with almost no repercussions despite a crime (underage) being involved shows he’s of a “protected” class.
Even though the French look away and sometimes secretly admire some ribaldry among/from their leaders, some things are a bridge too far. And Macaroon crossed that bridge years ago…
>>”abruptly yanked HCQ off the OTC medications list and out of pharmacies and drug stores”<<
“Emergency Use Authorization” may *only* be granted, lawfully, when there aren’t ANY other effective treatments / therapeutics / preventatives available.
This action by the French Ministry of “Unhealth” …
… demonstrates a *coordinated* effort, world-wide, to restrict access to time-tested treatments / palliatives / cures.
Medical censorship.
It’s absolutely a bona fide CONSPIRACY, both in theory and in fact.
ALSO, the Bat Lady, Chinese virus principal scientist Zhengli Shi, GOT HER PhD in FRANCE!!!
10/01/1996 – 05/11/2000, Ph.D, major in Virology, University Montpellier II, Montpellier, France.
AS WELL AS HER BIO-SAFETY TRAINING!
10/02/2006 – 10/23/2006, Biosafety course training in BioMérieux P4 laboratory, France
In 2006 Shi, Z. gave a talk: Bats are natural reservoirs of SARS-like coronaviruses. France- China Medical Symposium. Oct. 23-24, Paris, France.
In 2016 she received the Palm Knight Medal for Education from the Government of the Republic of France
WIKI
BIO:
https://www.ws-virology.org/wp-content/uploads/2017/11/CV_SHI-ZL-2018_ASM.pdf
Not to mention remdesivir, which now looks like absolute garbage.
Had two friends with the Covid (but at this point who can say who really had it), and they were both given remdisivir.
One had pneumonia. The other was really laid low. Typically didn’t go to hospital until then.
Anyhow, remdisivir did nothing for them. Long recovery in one case…like a month.
I tried to tell them about Ivermectin, but they believed the media lies at the time.
Thankfully both are fine now.
It’s intentional murder.
And most of the medical profession was in on it.
The medical mob is real.
I’m thankful that your friends escaped their pre-planned demise.
Me too. She is a dear friend.
Someone made money on it.
I hear that the morticians have a good business going. I haven’t sung a funeral since February, but have a feeling they are coming.
Yep. Things had been kind of dead for a while, but Tony the Tiny™ is looking to change that…
You’re wise to trademark that well-coined epithet!
It does everything a derisive re-nominative should.
And he does seem to have a Napoleon complex (among other substantial psych problems).
Nice pun-punch!
Have to wonder what vaccine caused the growth since 2015… Gates’s experiments in India and Africa? HPV? Ebola vax (if it ever saw the light of day)?
These deaths are the result of the actions of Dr. Anthony Fauci.
There are more than Fauci he is the so called bag man.
Absolutely, Dr. Fauci is a “front man” for the real puppetmasters / paymasters.
However, even if he himself doesn’t know ** everything ** related to the entire operation, he knows plenty enough to be interrogated at, say, Gitmo.
IF he isn’t Arkancided first…. Or is that Epsteined??
Yes he needs to be investigated. What a sad man and his wife is the ethics person for research what a pair.
Right Hand Rule — go to angles less than 0 degrees, and we break your finger; go to angles greater than 180 degrees, we break your thumb.
Another wonderful Saturday physics lecture. Heady stuff, well explained.
And as to things that turn… the kid helped with assembling a cabinet from IKEA yesterday, and he kept wanting to know which way to turn the screws. So I asked him to try and remember which way to turn the cap on a bottle to close it.
A litte nit: there is reference to a red and green arrow in the figures «5-5», but there are two green arrows, one along the axis of rotation, and the other parallel to it out at the point where the force vector is. Presumably one of these should be colored red?
Yeah, the one on the left should be colored red.
Back to the drawing board…or rather the drawing application! Thanks for the catch.
(I spotted an equally embarrassing blunder one of the figures for Part 2 Friday evening after I copied it to use it as the basis for one of these figures…and that was weeks ago.)
5-7 had the same issue, luckily I remembered it was “recycled”
In less than six months.
1oo days…
I just have to say, I’m enjoying that component multiplication example like one of those finger spinner things. I’m not moving on through your lecture, because I’m having too much satisfaction just marveling at the “essence” of vector multiplication which is shown by your ijk explanation.
Vector multiplication is somewhat intuitive by the right hand rule, but not fully, and not really. That mental concept avoids far too many of the numerical implications of what the cross product really is. Likewise, matrix multiplication is intuitively extremely unsatisfying – it provides the HOW but not the WHY. In fact, I’m almost convinced that the entirety of mathematics has been shortchanged by the matrix concept, and I sometimes wonder if there is a completely marvelous formulation of the same thing used “elsewhere” that might be vastly superior. In fact, when I read somewhere that Heisenberg’s “matrix mechanics” formulation of QM was understood by almost nobody, other than agreeing that it was correct, I felt a certain vindication in my despising the damn things. 😉
But I can dawdle over your example and “feel the mojo” of vector multiplication, and it’s really satisfying. It’s repairing a lot of “mathematical debt” that I incurred from the weaker points of some of my teachers, who were very good, but in some cases didn’t really convey the deep essence of certain things – for whatever reason.
So thanks! 😎 👍 🍷🐺 🎼 🔭
Dot-multiplication is just like regular multiplication – in involves a one-thing (magnitude) and another one-thing (same) to produce a one-thing.
Cross-multiplication involves a two-thing (direction and magnitude) and another two-thing (same) to produce a two-thing.
The problem is that “direction” isn’t the exact same thing as “magnitude”, even though they are both “measurable”.
It’s very much similar to the difference between the measurements (and motions) of “rotation” (circular) and of “translation” (linear).
It’s also similar to the “inexactness” of the integral (one must add an unknown constant “C”), as compared to the exactness of the “derivative” (no ad hoc addendum required).
Linear algebra may be of interest to you – it’s the basis for vector multiplication, and it explains the violation of the commutative property of multiplication (in matrices, A x B doesn’t equal B x A, except in rare (called “trivial”) cases).
As an example, a 4×3 matrix, multiplied by a 3×4 matrix, produces a 4×4 matrix.
But a 3×4 matrix, multiplied by a 4×3 matrix, produces a 3×3 matrix. Obviously the results aren’t the same.
Tenser calculus uses integration from one “metric” (a matrix, usually [x,y,z,t]) to another “metric” (the same shape matrix), instead of from one simple point (value) to another. It’s about as complex as one can get.
The “i j k” analysis Steve provided is a “short-cut” way of thinking – and very tough to grock unless one first has knowledge of linear algebra.
The “i j k” notation represents the three UNIT VECTORS which SPAN 3-D space; together, the three vectors form one of the simplest BASES to describe any vector in 3-D space.
Linear algebra is simply solving as many equations, with as many variables, as one wishes to.
Have three variables – x, y, z? One needs three equations to solve them completely. This is true no matter how many variables one begins with – the number of equations must match, or exceed, the number of variables.
If you’re into learning a bit about linear algebra, I suggest getting through Eigenvalues and Eigenvectors, but bailing out on transformations.
It’s actually pretty cool stuff, and I found it helps in understanding mathematics IN GENERAL …
Even whackier when talking about matrices. Depending on the dimensions, A multiplied by B might not even be possible. And if it IS possible, it’s still possible that BxA won’t be.
Technically what I showed was a mnemonic trick, not a real definition’ it was the trick I used a lot during my STEM education (we didn’t call it STEM back then but no matter). What you’re actually doing is calculating determinants, which in higher order matrices gets complicated, very quickly.
And linear algebra is definitely one of mathematics’ power tools, another one being calculus. It also takes a lot less “prerequisites” to get into.
“So I’m still wondering how Kepler did it.”
I think there was some angular momentum in his thinking. There was a force acting upon his consciousness, which moved his thoughts in a particular direction.
Really enjoying your openers. 😀
JOE BIDEN DIDN’T WIN!
Steve, I have to ask…..
…..is all of this just setting us up to hustle pool?
Nope.
Darn, I was hoping for a new revenue opportunity for the Tree.
Damn. That might have given me more incentive to keep up.
That being said there are things I have uncovered as I have been refreshing myself on this stuff, that would have made sense to know back then.
I know my college textbook spends over half its thickness on the kinetics, before even starting into electrical forces. I’m skipping completely over springs and didn’t really do much with pendulums, for instance; there are other topics like that. Not needed for where I’m taking this, but a more thorough look would definitely cover them.
I’m doing a lot of things out of order. That being said I’ve had to think ahead. I would have done the electricity post one week earlier but I realized I wanted potential in there and I was already packing too much stuff in there…so I went back to kinetics to get potential, then I didn’t have to explain it under electricity and magnetism. Likewise there’s something in this one I wanted before going further into electricity and magnetism.
This is all prerequisites for the good stuff.
Just another fun fact about the shots.
“Positron emission tomography (PET) imaging of cancer patients after they received COVID-19 vaccinations showed abnormal radiotracer uptake in lymph nodes, researchers reported.”
https://www.medpagetoday.com/radiology/diagnosticradiology/92800
In the LYMPH NODES?
That might explain why the 5 Doctors, I think it was Dr. Northup, talked about bathing in hot water laced with alfalfa with organic soap, and the nano-particles leave the body and gravitate to the alfalfa, I assume via sweat.
The lymph system is right under the skin. It’s the sewage system for the body. Does the human body recognize the nanoparticles as foreign and try to expel them the way the body gets rid of the rest of the junk?
The Chinese have used lymphatic draining techniques for thousands of years using Gua-sha tools. This is typically performed after prepping the skin with an oil, like jojoba oil. The head and face are the usual areas that is performed on, since these areas in Traditional Chinese Medicine link to every “meridian” (energy pathway) to the body.
The Native Americans have also used lymphatic drainage. They typically did this using a dry brush (even a piece of wood or a stick) on the skin, concentrating on the torso, arms, and legs.
I follow a family of chiropractors that use gua-sha as part of their treatment. I like the concept.
I do think the real solutions to good health are found in a crux of indigenous traditional methods and the old ways. Yes, we do need modern medicine for the big stuff, but to avoid that, the natural methods are preferable, IMO.
There are massage techniques that you can do to yourself for lymph drainage. We do them at home.
To herbally cleanse the lymph system, red clover or cleavers teas are helpful. They have been used thus for centuries.
One of the reasons I walk first thing in the morning is to get the lymph flowing. Plenty of water goes with it. Spring water, of course.
Also, I take baths of Epsom salts, baking soda, and black tea (just throw in half-a-dozen black teabags). This is a good detox bath, too.
I like dead sea salt and Pine needle.
Hot and cold showers.
I used to have body massages first bathing feet in warm water then body massaged with oil. Yes the spots on the legs behind the knee and the rest of the body also feet. I miss that because of covid.
Thank you for bringing up the alfalfa bath. I was super interested in that. Trying to find non-GMO ALFALFA is hard.
I wonder I bought alfalfa meal for my garden . Do not know what is in it.
Alfalfa is easy to grow my father in law did every winter. In spring he dug it over.
You can grow your own dry it like hay I assume and then when dry but it in the blender?
Alfalfa grows well in the north but not here in NC except in the mountains.
I did not know that.
Non-GMO alfalfa.
https://www.trueleafmarket.com/products/sprouting-alfalfa-sprouting-seeds?variant=14551733108851
How to Grow Alfalfa Sprouts
One barn I took lessons at grew oat sprouts to feed to the horses since they are much more nutritious that just oats.
Thank you!!
Well, I got logged out again.
But this time logging in sent me straight back here. That’s an improvement!
Whee!!! Improvement!!!
Sounds like he’s a beast, daily…
I didn’t realize they were thrown out!
.
If it were some blm/floyd crap the cops would have been posing with them for pictures.
TRUTH!
Here we go.
What better way to avoid talking about the Stolen Election…than with “UFO’s are real!”
They really think we are stupid…
Over here we actually have to pay for that drivel (ARD and ZDF, national channels). 18 Euro a month… no exceptions, unless you’re BOTH blind and deaf!
It’s just disgusting.
Pteromyini
All we have to do is say “Yeah – aliens are real – and they’re here to throw Democrats into JAIL.”
EXCLUSIVE: COVID-19 ‘has NO credible natural ancestor’ and WAS created by Chinese scientists who then tried to cover their tracks with ‘retro-engineering’ to make it seem like it naturally arose from bats, explosive new study claims
.
https://www.dailymail.co.uk/news/article-9629563/Chinese-scientists-created-COVID-19-lab-tried-cover-tracks-new-study-claims.html
Bannon is talking about this article right now.
Thank you!
I just put it up, and it seems that Peter Navarro is trending on Twister because of his comments (Fauci a mass-murderer).
“No credible natural ancestor”…
Sounds like Øbøzø….
cthulhu posted a link for Valerie Curren yesterday, and I wanted to re-post it in case anyone missed it. This is a very rational and excellent article on assessing the risks of getting a China virus “vaccination.” Wolf posted a similar type of article a few months back about vaccinations (real ones) in general. The post focuses on young people, but discusses everybody. I highly recommend:
https://market-ticker.org/akcs-www?post=242525
IIRC Valerie had been discussing her daughter (son? offspring?) taking the shot, and I believe cthulhu was responding to that.
Yes, and forgetting that she was blowing town for the hinterlands over the weekend.
FDA document reveals 86% of children who participated in Pfizer covid vaccine trial experienced adverse reactions

https://www.naturalnews.com/2021-05-27-fda-document-pfizer-covid-vaccine-trial-adverse-reactions.html#
……………….From the article:
(Natural News) A publicly-available FDA “fact sheet” document reveals that 86% of children who participated in a Pfizer covid vaccine trial reported adverse reactions ranging from “mild” to “serious.”
As part of the vaccine experiments, children aged 12 to 15 are being injected with mRNA sequences that take control of their cells, causing them to churn our spike proteins in their blood. Spike proteins cause vascular disease and blood clots. Even the Jonas Salk Institute conclusively identifies spike proteins as the culprit behind vascular disease and blood clots.
This is all openly admitted by the FDA, which has published extremely disturbing reports of adverse reactions experienced by children in a Pfizer covid vaccine “fact sheet” labeled 144413. See the original FDA document here (PDF). […]
Among those children injected with the mRNA vaccine medical experiment:
……………….More at link.
And parents are just signing their kids up for this.
Unbelievable.
Of course, since there has been such a pro-vaccine propaganda campaign ongoing for decades, not all that surprising.
It serves two purposes:
They prove they believe in Science, not religion, giving them cred with the “smart” people.
By using their children, they have a new way to virtue signal, it proves they are Super Parents, ingraining Science into their mini-me geniuses.
So many of the people I know who are submitting to their children being shot up are Church goers, though. They’ve steeped in the Kool-Aid.
Ahh, I see, I was speculating based on my “community”. Either way it seems like voluntary compliance to gain acceptance into the group, from propaganda like you say, as well as a decade of ubiquitous flu shots. For sure it is maddening to watch it go down.
This is in fact how superficial and easily manipulated half of America has become.
And the reactions, injuries, and future consequences (sterility, or birth of compromised babies / loss of, or impaired immune function / cognitive issues) to these children — are also the result of the actions of Dr. Anthony Fauci.
yesterday, barkerjim posted a link to an interview with Dr Peter McCullough, and I re-post it in case anyone missed it. It is very powerful. Wolf posted an interview with McCullough several weeks ago, and commented that McCullough was being circumspect and judicious in the way he stated things (Wolf was correct).
In this interview McCullough is much more forceful and direct:
https://ncrenegade.com/massive-world-renowned-doctor-blows-lid-off-of-covid-vaccine/
He really is not holding back in this video.
In the interview from several weeks ago you had to read between the lines, but in this one he is very explicit. He really is sounding the alarm.
Thanks for the tip!!!
If the chicom flu was introduced solely as an excuse to bring about the experimental jab, that puts a whole different perspective on things.
The amount of coordination / conspiracy there must be between the globalists is horrendous, and they can’t claim they were hoodwinked.
No better way to introduce universal contraception via a weakly bisexually contraceptive protein. It’s fairly ingenious – both the treatment and the ploy to make us all inject it.
I think he’s exactly right.
(poly = many, ticks = blood sucking bugs)
I’m borrowing that, thank you very much 👍
Why not, it’s already stolen.
The secret of originality is plagiarism.
There really was a mathematician named Lobachevsky, by the way….
Here are a few more in that vein (including a wonderful swipe at sociology, to the tune (and tone) of “Choreography” as sung by Danny Kaye in “White Christmas”) 🙂
Time jumps:
1:45 The Derivative Song
2:58 There is a δ for every ε
4:48 The Professor’s Song
8:25 Sociology Song
11:17 That’s Mathematics
Born in 1928. He’s still alive and kicking!
He was at UC Santa Cruz for a long time, not sure if he’s still there. Funny thing, his 60s liberalism actually seems conservative now…
With Brink-i-ley and Hunt-i-ley describing contrapuntally…
and “National Brotherhood Week”, and “Alma”…
Brilliant fellow. The comments on this vid are good…
….Non-Euclidean geometry . I did a paper on him back in the day.
That’s the one!
In fact, so was Riemann, mentioned in the song.
“Imitation is the sincerest form of flattery.
In the case of PDQ Bach, this flattery is known as identity.”…
– Peter Schickele, explaining PDQ Bach’s sometimes
thieveryidentical rendering of compositionsCatturd
@Catturd1h
·
When I was a kitten, my mom forced me to take pictures with my liberal cousin Hipturd – so embarrassing.

Verse of the Day for Saturday, May 29, 2021
✟
What shall we say then? Shall we continue in sin, that grace may abound? God forbid. How shall we, that are dead to sin, live any longer therein?
Romans 6:1-2 (KJV)
Thank You, Jesus, for blessings received and prayers answered!!!
BE MY VOICE
🦋 🦋 🦋 🦋 🦋
When I was learning to drive, my dad made me learn All The Things required for maintenance, including changing all four tires in the driveway while he timed me. He gave me a metal pipe about 3 feet long that I would slip onto the jack handle to increase the torque. Easy peasy lemon squeezy. He also taught me how to hold and swing it to use it as a weapon, and made me keep it in the trunk in case I needed it on the side of the road one day.
He’s a great dad, but man he was hard to live with if you were a teenager 😂
He drilled you a lot, but it was on practically useful stuff. And that bit about increasing the torque, well obviously you got reminded of it somewhere. The stuff works!!
Yes!! Thanks for the memories. Maybe you didn’t see me in back of class this morning, waving my hand, saying “pick me Teach, I know this one”. I wish I still had that metal pipe. About ten years later some moron hit me and the insurance company totaled the car and hauled it away before I remembered to get it from the trunk.
I think those two kind of go together 🙂
(“Train up a child” and so on…)
And eventually, you are rewarded with teenagers of your own 🙂 or 😮
That’s the truth! I’m only lucky enough to have one, mostly 🙂 but enough of 😯 to keep me on my toes. He and my dad get along like a house on fire lol, I just shake my head and say “You’re getting soft old man”…he says “You’re allowed to get soft when you’re my age”
Barr actively interfered with private investigation about election fraud:
Let that think in – How corrupt was Barr really?
SCOOP: Private Investigator Says AG Barr Told Him to Stop Investigating Election Fraud Claims (electionwiz.com)
https://twitter.com/i/status/1398427487319871493
Full Video:
https://youtu.be/YabgDDsOU5U
Wow. Just wow.
Bagpipes should be questioned under oath as to why he did that.
Interesting that we are just hearing about it. Things must be moving.
Hold on, folks. Do we have ANY evidence for this other than Tony Shaeffer’s word?
Even so much as an affidavit?
In point of fact, this is actually hearsay, since it’s Chase Geiser saying Tony Shaeffer told him something.
NICE CATCH!
We really really have to keep an eagle eye out for possible dis-info.
I recall an exchange here with someone who was relying on a certain Guy on the Internet. When challenged, it was brought up that someone had tried to silence the Guy on the Internet.
How did we know this, I asked. The Guy on the Internet had said so.
It seems I was the only person who had wondered if the Guy on the Internet could be lying about that in an attempt to increase his cred.
I dunno, I tend to believe LC TSPOOKY. He was silenced before, about Las Vegas. He was on Fox saying that they released the pictures early on purpose for a nefarious,misleading?? reason and that there was a lot more going on that they weren’t telling us. Daily I looked forward to his appearances on Martha’s show for more scoop but he was disappeared shortly after that interview. 🤔🤔 AND I’ll never forget the fact that De Santis, who at the time was Head of Homeland National Security Committee, dropped everything and flew to Vegas within hours, then crickets.🦗🦗 Insert 5,000 Suspicious Cats.
They could have been pulled by the White Hats.
Don’t forget, we are where we are with the audits, the scamdemic and more because of the specific way the events have fallen. A lot of the “good guy efforts” reported to have been derailed would have put YOU ARE HERE in danger of truth exposure too soon.
I have reasons to believe that this was done so that a 9-11 level scare event will open minds to the transmission of truth rather than a preplanned narrative. Just watching the way the various anons are reporting information, it seems like shock will be necessary to overcome the brainwashing.
Nothing like REALLY HURTING to bring home how nasty the Cabal is.
It is very difficult to let things happen that kill people but sometimes that is what it takes to win a war. Never forget that POTUS Trump spent five years in a military school. Although he never served, due to the heel spurs, he had the MILITARY TRAINING to understand that.
The USA was slowly being bled to death and BRAIN WASHED so we would never notice our country was being taken by stealth. Given that brainwashing, a major ‘dislocation’ and even deaths are needed to get people to WAKE THE F…K UP!
I know the deaths of innocents is very hard to handle, but in this case I think it is absolutely necessary to bring home the fact WE ARE AT WAR!
Senior Member of CCP Think Tank Claims China Won Unprecedented Biological War Against the US in 2020 and “Put the US Back in its Place”
PRAYING ON THE ARMOR OF GOD
Father God, I now follow your command to put on the full armor of God, because my battle is not against flesh and blood but against rulers, authorities, the powers of this dark world and against spiritual forces of evil in the unseen world.
I first pray on the Belt of Truth that it may be buckled around my waist, may I be centered and encircled by your truth dear Lord. Hem me inside all that is true and right, and may I be protected and held up by the truth of your living word, in my Lord Jesus name.
I pray on the Breastplate of righteousness, please protect my vital organs and my inner man, cover my integrity, my spirit, and my soul. Guard my heart for it is the wellspring of life, please strengthen and guard the most vulnerable places in my life with that which is right, good, and noble that I might not receive a fatal blow from the enemy, in my Lord Jesus name.
I pray on the Gospel Shoes of Peace. I choose to stand in the shoes of your good news, and on the firm foundation of my Lord and Savior Jesus Christ, the solid eternal rock. All other ground is sinking sand, I pray that I will not slip or fall, but that my feet would be firmly fitted on your lordship, my Lord Jesus. I choose to stand on you, so that the peace of God, which transcends all understanding will guard my heart and mind in Christ Jesus, the eternal Rock of Ages. I receive your holy peace now my Lord, from the sole of my feet to the crown of my head, in my Lord Jesus name.
I pray the Shield of Faith into my hand now. As I take up the shield of faith, I ask that you might extinguish every dart and arrow, that is launched from the enemy to take me down spiritually, physically, mentally, emotionally, and every attempt of the enemy to destroy my joy. I ask that my faith in you would make it flame out. Extinguish every flaming arrow that would come against me, my life, my family, my home, or my ministry. May my faith always be out in front of me like a shield. Give me the courage to “faith my fears” by choosing to walk by faith and not by sight, in my Lord Jesus name.
I pray on the Helmet of Salvation, that you might protect my mind from the thoughts that can lead me astray. I choose to take every thought captive, and arrest all intentioned ideas and motives that would harm others, or distract me from your holy will for me. I submit every captured thought to the Lordship of my Lord Jesus Christ, and ask that you would imprison those thoughts that are not of you my Lord. Transform my mind and renew my thinking that I may think God thoughts, and have a sober mind that is focused on your glory. Please protect me from being double minded that I may allow my mind, I reject to live an earthly life, because I choose to live a holy one, governed by you My Lord Jesus, the prince of peace, please have my mind to be saturated with the holy mind of Christ, in my Lord Jesus name.
Finally, I take up the Sword of the Spirit which is the holy word of God, I pray this powerful offensive weapon into my hand, and ask that your holy word would be fitting for every encounter I face. As the enemy gets close to me, please give me the insight, wisdom, and skill to wield the word of God to drive away the enemy, in my Lord Jesus name.
May the enemy and his team flee from me, upon hearing the word of God spoken by the power and direction of the Holy Spirit. Give me the sword of the spirit to cut through the wiles of the devil, so that I may discern the schemes of the enemy when he is near.
With all kinds of prayers, supplication, and intercession I pray to you my Lord God as the one who fights my battles. Now that I’m in your holy powerful armor, I walk away covered and ready to face my day as you go before me, and please protect me in the midst of the spiritual warfare in this unseen world, in my Lord Jesus name.
Thank you my Lord, for the spiritual weapons of armor and prayer that you have given me. It is written no weapon formed against me shall prosper, and you will refute every tongue that accuses me.
Thank you Father God, my Lord Jesus and the Holy Spirit, that I am more than a conqueror in my Lord Jesus. I pray all of this in the mighty name of my Lord God and Savior Jesus Christ, amen.
𝕁𝕠𝕖 𝔹𝕚𝕕𝕖𝕟 𝕕𝕚𝕕𝕟’𝕥 𝕨𝕚𝕟.
Quick, how many radians around each of those circles? 😀
I’m RETIRED!
Yeah, but you don’t need to do so much as one calculation!

Quick, let me grab my CRC chemical handbook…..
Why? Did you forget your daily exercise?
No, it’s in a
beakerglass right next to me 😀(or, to paraphrase Dorothy Parker, I’d rather have a bottle in front of me, than a frontal lobotomy… or wrt CRC, “this is not a book to be tossed aside lightly; it should be thrown, and with great force” (ibid) )….
For extra credit, erm, workouts, I have the Oxford Unabridged, from the early 1960s… (before they reduced the size and the typeface to like 4-point or so, and included a page magnifier)…
I have one of those, by the way, dating back to the 1950s. Belonged to my dad in college, methinks.
Well, the one in the foreground in blue looks like a weighty-Anne to me…
(or maybe the trans-health secretary)…
https://gab.com/JovanHuttonPulitzer/posts/106318805025910597
Pulitzer has a link to the trailer.
(I don’t know why that little arrow is on the image. Pulled from WATNews 🤔)
Maybe it’s a screen shot – looks like the standard M$ cursor…
Coal Fired Power Dying – Not So Fast – Part One – Introduction | PA Pundits – International (wordpress.com)
AntifaBook.com (@JackPosobiec) Tweeted:
BREAKING: AMC, Cinemark and Regal Cinemas remove mask mandates https://t.co/scKsqk3Huk
But only…”for people who are fully vaccinated”?
Those pronouncements drive me nuts because their implementation makes no sense. How are they going to know who is “fully vaccinated”? Are they going to risk becoming known as the business that is segregating its customers, or, worse, denying service to some? And are they going to ask if people have had their full complement of two vaccines, making them “fully vaccinated”? Of course not. They are just going along with the narrative without having to actually enforce the rules or do anything to put themselves at risk.
They want people divided according to inoculation status, and they are putting the burden of doing that on us. No way am I playing that game. If they want to know my status, they can ask, directly, and suffer the consequences — which could entail having others hear the exchange, to getting the news media involved, to getting Congress people involved, to lawsuits. It’s not good for business, which is precisely why they’re trying to make us do it for them (in addition to conditioning us to be sheep). Not playing.
I am identifying as vaccinated.
Me too. And that’s all they need to know. 💉
Hubby keeps saying that too. 😋
Vaccinated, Immunized, whatever. Doing the same 😉 , has been micro dosing for nearly a year and a half.
And then to not be and be within spitting distance of someone who is is asking for trouble.
Yes, I will self segregate to keep away from the idiots.
I wonder how long that will go on. I think someone (cthulhu?) posted that 35 days after inoculation, the danger of spreading is over…maybe? Of course we know the inoculation status of some in our circles, but how would we know about others? It seems that the need to stay apart could go on indefinitely, seriously curbing one’s freedom of movement.
What I posted was a link to one study that indicated that the amount of shed proteins might decline with time, so as to be negligible after ~40 days.
Of course, one thing this whole exercise has conclusively shown is that any one study may well be an anecdote.
YES!!! I want to see several WELL DONE studies.
Wonder what they will do with people who are in a control group? I was accepted into a control group a couple of days ago, doctor group in Syracuse. I didn’t wear a mask in Walmart and no one challenged me.
They arent going to check….
Chinese scientists created COVID-19 in a lab and then tried to cover their tracks, new study claims | Daily Mail Online
A lot of information in this article.
Ha Ha Ha!
.
https://twitter.com/AmericanaMama_/status/1398463784432381960
Ouch, poor Aubergine!
That’ll probably make her purple with rage 😀
And then there’s CatTurd’s meme of telling Kamel-hoe that “IMAHOE” isn’t an Indian tribe…
Our previous Governor had a mistress who was not well respected by many of the citizenry of the state. In many circles she was referred to as “Miss I-da-ho”
Why is Energy so Difficult to Store? Why is Stored Energy so Difficult to Use? – Watts Up With That?
We can use the physics we are learning to understand the concepts.
Good article!
Any storage scheme is going to take its “cut” of the energy stored as losses. If we could find a truly good scheme it’d be a wondrous thing and I say that not even thinking about “renewables.” It’s far cheaper to design conventional, green-hated electrical plants if they don’t have to have an adjustable output, and if we could store excess power produced at night for use during the day, that alone would reduce energy use without any hit on our standard of living. So it’d be of benefit for that as well, ironically for the opposite reason (allowing you to generate a constant rate, rather than being able to generate at a variable rate that’s not convenient, like with renewables).
A very good lithium-ion battery can store 260 watt-hours per kilogram. (At the low end they store 50 watt hours.)
A watt hour is a watt, for an hour, and is thus 3600 joules (a joule being one watt, for one second). [watt-hours are one of those sort-of-metric units you need to convert to the standard metric units, not hard to do but annoying; electrical energy is sold by the kilowatthour, 3.6MJ per each.] So this good battery stores 936,000 J and weighs one kilogram. It’s just a bit less than one megajoule.
Gasoline stores FORTY FIVE megajoules per kilogram. And to add to that, a kilogram of battery is pretty damned expensive. The reason these whacky mechanical schemes (compressed air, all kinds of variants of mass pushed uphill, and so on) were attractive was because as bulky and ridiculous and thermodynamically inefficient as they are, they’re a lot cheaper than a bank of batteries.
Batteries SUCK, basically.
IIRC there was a long discussion about that at ChiefIO or Tony Heller’s. The only half way viable storage is to use wind/solar power to pump water up to a reservoir and then use the water to generate constant electricity.
Yeah, that’s my “favorite” of these ideas, but even there, you need non-flat terrain! Of course, we *do* know how to move electricity over long distances, but it’s another source of loss.
And, over at NoTricksZone (Pierre Gosselin’s site), Kenneth Richard details the futility of Germany (and other countries) abandoning coal and nuclear, when Red Chyyyna is building one new coal plant PER WEEK, and quite a few nuclear plants as well…
https://notrickszone.com/2021/05/27/whats-the-point-in-2020-china-built-the-equivalent-of-more-than-one-new-large-coal-plant-per-week
Here’s a little chart (click to embiggen):
Just looking at the trends (down is us, up is the Chyyyyneese), it’s obvious we’re losing this “battle”, and effectively funding Red China’s growth and world dominance…
Ground report.
Grocery stores and the like do not have signs posted, yet many wear the masks. Whether they’re doing so out of sheer force of habit or because they haven’t been vaccinated and think they are being good citizens is another question. I’ve certainly not gotten any “Karen” responses from anyone there.
Smaller places I sometimes have to do business with, on the other hand, are still displaying “wear a mask” notices without an exception noted for the vaxxed.
One place is actually posting “wear a mask unless you’ve been vaccinated” signs.
To be honest I haven’t paid much attention to the directives from our Polis-state governor, so I have no idea what the actual current Polis-y is.
I have known this man for years and never believed the accusation made against him. I’m glad the charges were dropped, but she should have to pay for what she put him through!
.
He can counter-sue for the attorney’s fees MINIMUM and for distress and tarnished reputation. I hope he does!
Video of health related professionals from around the world who state (one after another) that there is no actual global pandemic, and that the “vaccines” have not been proven safe and effective, and in fact are highly risky:
This video is not really informative or educational, it is a cry of alarm and warning. In this respect, it is similar to Dr McCullough’s warning posted by barkerjim.
1) I chuckled to myself thinking how, ironically, MAGA Deplorables will constitute a majority of survivors, until it occurred to me that the probable coming world will be Hell, regardless of who survives;
2) The most significant point (to me) Dr McCullough makes (in the video posted by Wolf a few weeks ago and the other video posted by barkerjim yesterday) is about therapeutics. Not only did TPTB not focus on therapeutics, they tried to make therapeutics impossible even to discuss, let alone try. To my mind, this proves their evil intent more than anything else, although their evil intent is inferable from numerous aspects of their ongoing Fakery and Coercion;
3) It looks like the End Game is here. The Satanists/globalists/communists/plutocrats, whoever, are all in. They are all but open and mocking in their blatantly fraudulent machinations and Fake Reality;
4) I see many on our side making guesses about electoral politics, mostly optimistic, and I truly hope they are on to something. There is certainly no reason to abandon the trappings of normality at this point, especially when we are at a huge, practical disadvantage in our daily lives. I simply believe, and could be wrong, but believe we are way past electoral solutions;
5) Substitute “because we are going to rule over the world” for every phony and fabricated reason they give for anything they do (and it is 100 % phony and fabricated, in your face phony and fabricated). It would normally be impossible to tell if their blatant lying is posturing or a genuine expression of might, or to what degree of either, but when I consider how they effectively control all the powerful institutions, and control half the minds in America, I think they are doing what they know they can get away with, without harming their position. IOW they can laugh in our faces, knowing that we know that they know that we know that they know. The essence of their sadistic desires;
6) I recently read a book named Friends Divided, about the friendship between John Adams and Thomas Jefferson, who disagreed on almost every issue, big and small. Unlike Jefferson, Adams foresaw what would happen to America eventually. Adams knew that America depended on the virtue of her citizens, and he knew that men were weak and sinful. Adams foresaw that corrupt, avaricious gluttons for power could use America in precisely the way America is being used now. He was prescient;
7) In thinking about the many institutions and corporations under the control of TPTB, the breadth and depth is breath-taking. It seemed to happen over night, but it did not. That thought, too, is breath-taking;
8) One of those institutions is the pharmaceutical companies. As recently as a year ago, a person could reasonably think they were merely greedy, amoral pigs, who at least produced things of benefit. Now it is obvious they are that, AND they are active players in the destruction of America for political purposes. Breath-taking.
On point 1, a lot of deplorables believe the vax stuff, so perhaps not. Also, the third world is not getting vaxxed nearly as much, so what we’d be heading for is even fewer of us to man the Wall.
Perhaps this is what Q meant when he said they will not be able to walk the streets.
If you hear about sex trafficking of minors or cannibalism, it does NOT have the same impact that spending a YEAR under ‘house arrest’ losing your business, watching your elderly die… AND then finding out it was a COORDINATED ATTACK by the Chinese/American CABAL on the USA.
This is how it needs to be done.
1,000 Lawyers and 10,000 Doctors Join Together and File Lawsuit to Prosecute the “2nd Nuremburg Tribunal” Against Corona Fraud ScandalBy Joe Hoft
Published May 29, 2021 at 9:32am
1,000 Lawyers and 10,000 Doctors Join Together and File Lawsuit to Prosecute the “2nd Nuremburg Tribunal” Against Corona Fraud Scandal (thegatewaypundit.com)
Left Attacks Trump Appointee Who Dares Tell the Truth: Immigration Is Used to Replace White Americans.
What can often get you in far more trouble than telling a big lie is telling a big truth. And it can really put you in hot water if it’s a big truth that threatens big power. Colonel Douglas Macgregor (ret.), a decorated Gulf War veteran–turned–consultant and commentator, is learning this the hard way.
.
The 68-year-old Macgregor, you see, has had the temerity to mention that Democrats are using immigration to effect demographic change that will help them win political power
.
https://thenewamerican.com/left-attacks-trump-appointee-who-dared-tell-the-truth-immigration-is-used-to-replace-white-americans/
They’re doing the same thing here, only using Moslems as the “replacement army”…..
Merde-Kuh, et. al. don’t care: they don’t have any children…
I hope he wears it like a badge of honor.
https://twitter.com/LadyPie6/status/1398671997425655810
Truly a good thing he did revealing FB censoring. Kudos for going public. He had to have known he’d get canned from FB. Rather sure he has already lined up employment elsewhere.
Probably on Caturday, too…
This is Fabulous. 😂 FIGHT BACK!!
California Restaurant Charges Patrons Extra Money if They Wear a Face Mask, Brag About Their Vaccine Status (thegatewaypundit.com)
nd speaking of aliens ?resize=580%2C586&ssl=1
?resize=580%2C586&ssl=1
Hunter Bye, Done and that creepy congresswoman from Kalifornistan?
(or, shudder, “Nick Danger” and Elizabeth Warren…)….
Five Docs from Thursday.
https://www.podbean.com/ew/pb-pqp88-104d674
<iframe title=”CRITICALLY THINKING w DrT and DrP – SPECIAL EVENT – The 5 Doctors Discuss Personal Approaches to Health” allowtransparency=”true” height=”300″ width=”100%” style=”border: none; min-width: min(100%, 430px);” scrolling=”no” data-name=”pb-iframe-player” src=”https://www.podbean.com/player-v2/?i=pqp88-104d674-pb&from=embed&square=1&share=1&download=1&skin=1&btn-skin=7&size=300″ allowfullscreen=””></iframe>
Well, that didn’t work, either.
The Five Doctors are: Dr. Lee Merritt, Dr. Christiane Northrup, Dr. Carrie Madje, Dr. Sherri Tenpenny, and Dr. Larry Palevsky. We have taken a stand together to educate and clarify the ongoing issues of this Plandemic, the fight for your lives, your mind, and your very soul.
In this episode of The Five Doctors Speak Out:
Dr. Lee – gives a big picture overview on why we don’t have clear answers.
Dr. Christiane – talks can you tell us a little bit about why people are using white pine needle tea, anise, fennel, and citrus rinds as a source of schikimic acid, a pathway responsible for the production of vitamins and certain amino acids.
Dr. Carrie – explains what she is personally doing to avoid EMFS and to detox her system.
Dr. Sherri – tells why children and teens absolutely should NOT receive this injection and the approaches she personally is using to safeguard her health
Dr. Larry – takes the discussion home with how we can move forward through these tumultuous times.
Stand on the Earth to decrease the electomagnetic effect on the body.👀
Maybe for those who spend a lot of time working in an office would benefit from having an anti static mat on their desk earthed to any convenient place.
I’m about halfway through, and the highlights:
Dr. Merritt got too close to someone who had recently been injected, and had a nosebleed to end all nose bleeds that she stopped with HCQ and she was quite impressed with that.
Dr. Northrup advocates the citrus simmer HCQ substitute and is willing to try white pine needle tea. Fennel and anise are also mentioned. All women of child bearing years, pregnant or not, stay away from the injected, and refuse all injections while pregnant, and NO hepatitis B shots for the baby. Also, walk barefoot on the earth for 20 minutes a day for some electromagnetic something.
Dr. Tenpenny talked to a nurse who reads charts and the nurse has been reviewing the charts for the shot up. It seems that the worst of the reactions are girls/women using Nuvaring for birth control. Dr. Northrup said that that issue has been known with Nuvaring, and that the clotting issues involved with artificial BC are going to be magnified.
All three are seeing defiant independence among the 20-something crowd bound and determined to get the shots. The kids will not listen to anyone speaking against it.
Really, these people are on top of the issue.
My first citrus peel concoction is simmering on the stove. At this point, I’m just going to have to do it along with all the other preventatives. I’m not in an office situation, and can avoid public restrooms, but will be in Church at least a couple hours a week in multiple buildings for the next few weeks.
Go ahead, get and take HCQ & Ivermectin weekly.
PROTECT YOUR DNA!!
I’m having a rough spring allergy wise. I’m just hoping that’s all it is.
I’ve been taking Serrapeptase for about 6 months now. Blood cleaner, scar tissue dissolver, mucous thinner. It really helps with my allergies, stopped my eyes and nose from watering nonstop. I still take zyrtec daily, but most days do NOT need additional Sudafed. Before the SPEP, I’d need 3-7+ 30mg Sudafeds daily.
After a NASTY sinus infection that had me on juiced up antibiotics and then steroids for the reaction, I refuse to do any OTC or scripts. Someday, maybe, I will need them, but for sinus issues, I Neti-Pot, use salt water sprays, and have ways to get through them.
Now that I’m listening to Dr. Carrie, I’m paranoid about the bottled water I buy by the case. It’s on the fluoride free list and a friend who is an Evian drinker will only use the label I buy as a substitute.
I’m also now thinking its a real boon to live in a gray area when it comes to cell towers.
She and her handful of 25vitamins and supplements. Now I don’t feel so bad about my cabinet full!!😁 Every day I lay out my piles. I also have a daily planner with a checklist of all meds and supplements, so I can keep track of what all I’ve taken. If I get symptoms I go back and check to see if I’ve had too much or too little of something. I also keep track of food, appts, etc…. My life is in my book, It keeps me organized!
She’s taking Nattokinase too. You can get a Spep+Natto combo supplement. Both are similar. Now I’m going to get some Natto.
Research shows serrapeptase possesses significant anti-inflammatory, proteolytic (protein dissolving) and fibrinolytic (fibrin dissolving) properties. It reduces scar tissue, improves tissue healing and supports a healthy respiratory system. Nattokinase has powerful anti-inflammatory and fibrin-degrading activity. It prevents and dissolves blood clots, promotes healthy circulation, and supports normal blood pressure. It also helps maintain healthy C-reactive protein levels (CRP). CRP is an inflammation marker and a serious risk factor for heart disease.
SerrapeptaseNattokinaseHistory of UseSerrapeptase is a protease that has been used in Japan and Europe for over four decades for its anti-inflammatory activity.
Natto has been known for centuries for its positive medicinal properties, particularly for cardiovascular disorders. A researcher, Hiroyuki Sumi, identified the active enzyme in natto and showed its ability to dissolve blood clots.
Where do they come from?Serrapeptase was originally derived from a species of bacteria called Serratia mercesans, which is found in the intestine of silkworms. The bacteria produces an enzyme that enables the silkworm to dissolve its silken cocoon and emerge. Serratia is now grown in cultures and fermented to produce serrapeptase.Nattokinase is derived from natto, a traditional Japanese food made from fermented soybeans. To make nattō, soybeans are fermented with the beneficial bacteria Bacillus natto. During fermentation, the Bacilli produce protease enzymes, the most important of which is nattokinase.
What do they do?Both serrapeptase and nattokinase are widely known for helping the immune system respond to chronic or acute injury. These systemic enzymes act on protein-based complexes such as fibrin in scars around damaged tissue. Fibrin performs an important function in the body, including clotting and wound healing. However, excessive fibrin build-up in the body can impair normal blood flow which may lead to increased blood viscosity, swelling, edema, pain, inflammation and more serious cardiovascular problems. People with pulmonary fibrosis experience low oxygen levels in the blood and breathlessness due to excessive fibrin build-up in the lungs. This extra fibrin thickens and stiffens the lungs and blocks healthy oxygen and carbon dioxide exchange. This is why supplementing serrapeptase and nattokinase can help your body to relieve symptoms caused by too much fibrin build-up.
Research shows serrapeptase possesses significant anti-inflammatory, proteolytic (protein dissolving) and fibrinolytic (fibrin dissolving) properties. It reduces scar tissue, improves tissue healing and supports a healthy respiratory system.Nattokinase has powerful anti-inflammatory and fibrin-degrading activity. It prevents and dissolves blood clots, promotes healthy circulation, and supports normal blood pressure. It also helps maintain healthy C-reactive protein levels (CRP). CRP is an inflammation marker and a serious risk factor for heart disease.
🚨 🚨 WOLFIE!!! 🚨 🚨
May help reduce scar tissue in lungs.
My allergies have been thru the roof. O2 down to 90% this morning again UGH!
Grass here is outrageous. I think that is what is doing it.
Here too. We need to MOW! But it is tough to work when you can not breath.
Exactly. Freshly mown grass sends me into asthma and other assorted issues.
OMG!
Lots of women use Progesterone cream during and Post Menopause to alleviate symptoms. Christian television channel Daystar promotes it.
Nuvaring also contains progestin.
Why does progesterone cause blood clots?
Birth Control and Family Planning
Birth control methods that contain estrogen (i.e., birth control pills, patches, and rings) and synthetic progesterone (progestin) can increase a woman’s risk for blood clots because they cause an increase in the level of clotting factors or clotting proteins in a woman’s body.
Knowing your body and going the natural route is not vogue right now, but maybe God knew what He was doing.
GOOD GRIEF!
Use vitamin E and Co-Q-10. (If I quit for a week I get hot flashes again – a Real PIA here in NC)
❤️ this comment. Seriously had no idea, would love to know more details.
Lots of support for saunas.
Liquid cilantro, silica (Figi Water has lots of it).
Vitamin C. Pine needles have the highest concentration. Interesting.
Magnesium, B12 help to detox. (Red meat)
Another reason they want to get rid of beef.
Dr. Tenpenny connects the dots for the ones pre-pubescent getting the shots and transgender, etc. She doesn’t say it, but it sounds like interchangeable eunuchs.
Ugh. Nauseating.
The nurse is seeing both types of heart attacks from the injections.
People have chosen to defile the body that God made. (See skin ink for the precursor to this. Drives me batty.)
I can tolerate the skin ink, but it’s all the piercings and shit that get me.
Yeah, don’t like those, either.
Gateway Pundit is reporting on this article from March (so it might have been posted here then): https://humansarefree.com/2021/03/legal-team-wants-second-nuremberg-tribunal-to-try-global-lockdown-promoters-for-crimes-against-humanity.html
“Should the technocrats who pushed governments to lockdown their citizens be tried for crimes against humanity?”
_____________
Cart before the horse.
The question should be, “Should the technocrats and politicians who pushed lockdown on their citizens be ARRESTED >> RIGHT NOW <<, before the sun goes down, for crimes against humanity?”
It needs to be URGENT, compelling immediate action, not theoretical.
https://qalerts.app/?n=4954
.

EDIT: Nevermind. Will post new comment.
2021???
Last drop was 12/8/19 #4953 .
No ResultsNo Q Post with number 4954 was found. If this is a recent Q Post, try refreshing this page in a minute or so.
Maybe you meant to say 12/8/20. 😁
Why Yes, yes I did, thanks for the correction TT!!🥰
Alright, this drop was posted to Q’s private board here.
https://8kun.top/projectdcomms/res/20.html#111
Jim Watkins (8kun owner) claims it might be a test comment.
https://gab.com/JimWatkins/posts/106320282599778147
Not sure what’s going on. Whatever it is, it’s calling itself “B” and not “Q.”
Yeah, I’m massively skeptical. As in almost totally.
B for Biden?
Well, that makes me fascinated.
Waiting for further instruction on this one. If it’s authentic, the audience for it is VERY small, and I don’t think we are it.
Feisty cat thread says this is a BlueAnon hack.
https://twitter.com/CHHR01/status/1398766424886329346
https://twitter.com/CHHR01/status/1398754003878662148
I can’t make heads or tails of that, and I don’t know what a blue anon is, but I trust that those in the know have outed someone trying to make fake Q posts.
I’ll put this up on today’s daily also, but this is a possibility.
https://twitter.com/Littleb29872980/status/1398961274961211398
🤨
.
.
And I thought Catholic religious education was pathetic. Ugh.
This is just outright predatory subversion, intentional anti-Christ activity.
I’ve never believed there was a rover on Mars. The government gives NASA a billion dollars, NASA pockets and launders the money for whatever black budget project needs it, and then they release pictures from Devon Island or Arizona to the public claiming it’s “Mars.” Pleased to see that most of the comments on Zero Hedge agree with this theory.
And, in the distance, you can see a few pallets (boxcars?) of freshly-printed ballots for Bye, Done…
Nonsense, Mars is red.
Very well read, I’ve herd 🙂
(Alls Wells that ends Wells)…
LOL! I must warn that an insanely large percentage of the commenters on Zero Hedge are Russians – and I’ll bet the Chinese are pretty thick, too. Dig under the NASA disinfo window dressing, and you’ll find the fentanyl of flat Earth pretty quick.
I’ve studied the “flat Earth disinfo community” for too long. It’s pretty sad what they’ve been able to do to us.
The problem is very deep. Because of denial requirements on “Foreign”, Americans have no concept of the near universality of physics and chemistry phenomena in the universe – nor the extreme age in which that universality operates. Combine that with all the other deceptions long in operation, and the POWER retained by keeping “Foreign” off the public table, and it means Americans are BABES IN THE WOODS for smarter players.
The Bidenoids would not pull out the “alien disclosure card” if they didn’t have to, and IMO they’re teetering on it. Dems are absolutely desperate to be the ones in control. IMO that was one of the big reasons they stole the election. They see disclosure as a threat to their power for some reason. I’m not sure why, but I’m sure it’s true, and that it’s one of the motivations for recent military disclosures.
A very good perspective, even though I’m not 100% in her camp, one might say because of tribal background. Having quality weapons by the crate always results in a more honest deal, as long as oneself is an honest player.
Bottom line – sister planets of same type in same system are gonna look alike because same chem and same phys.
Mars makes sense, and the ChiComs are smart. THEY want to lead there. They know the potential – like TRUMP does. And they will dumb us down until we’re their slaves in the mud to take control.
Here’s something you don’t see every day in Earth deserts.
https://phys.org/news/2016-11-curiosity-space-metal-meteorite-surface.html
See also:
https://phys.org/news/2014-07-curiosity-heavy-metal-meteorite.html
There is an interesting SIMILARITY to Earth processes, but the items are just a bit alien. BIG, too. Huge difference in gravity and atmosphere – again – similar but different in easily understandable ways.
I’m not arguing Flat Earth or even ruling out possible secret black budget Mars exploration going on over there. All I’m saying is that I find it far more plausible that they’re releasing Photoshops in exchange for billions of tax dollars than them sending a machine tens of millions of miles away, and have that machine still working and looking in pristine condition eight years later. We’ve been lied to about everything else, and I’ve got zero reason to believe that they’re suddenly telling us the truth on this one.
After going to a bunch of NASA websites just now and looking at their raw data, I am personally assured that it’s all genuine – BUT – I will split the difference with you.
NASA management is clearly engaged in what might be called “mutual sandboxing” with the real science people. The scientists do what they need to do, and capture an insane number of scientifically fascinating but otherwise boring raw images and technical photos. The whole op has the tells of unmistakable reality to me. BUT management can’t really use most of it. SO there is a certain amount of “marketable shot production” that seems to be mandated, where people outside the scientific nucleus do stitching, panoramas, “illustrations” (Photoshops) where they sometimes even say “Illustration”….

….. in order to churn public interest for cash.
This is why all the images of clouds and whatnot that appear in these articles are months old, and out of sync with news about what’s actually happening with these rovers.
I have some insight on this from a prior employer in “fake science”. When I started with them, they would actually trust chance, and whenever a “showcase event” happened, and we had something newsworthy, the random event would be given to the press. This was actually very cool, because the press would get some insight into random real science.
Well, well, well. It took management a while to figure out how to lie without lying, but sure enough, it’s possible.
When they knew they had a “random” event due, they would have the entirety of relevant management waiting like hawks with PRE-PLANNED INSTANCES of “newsworthy” to throw into the system as the event window approached and began, so that – OMG – the newsworthy event is super-newsworthy, and would feature some corporation, some client, some friend – you get the picture – it was all very “real” and slighty random but still FAKE AS HELL. Of course, that fake became very obvious to us on the inside. Management would find stuff, grab stuff, hold stuff, and dump stuff passing through the system to game the outcome.
So that’s what’s happening here, IMO. NASA management is “sexing it up” to impress people. They may even be holding publications and announcements from the press to varying extents in proportion to how much publicity they can milk from it. And you can bet that if they find that first fossil – which may have already happened – it’s gonna be a LONG TIME before that gets out.
IMO they’re probably now using Curiosity for the “sexy pictures” because all the science heat is going to be on the new lander. AND – very important – IMO that was planned years ago. The scientists sacrifice the old lander for tourist pictures. Management sacrifices the new capabilities for the scientists to announce big stuff without pictures. And that serves double interest by slowing down anything really big that they find.
Zuckerborg 😳

The look of a ChiCom puppet!
He’s a puppet’s puppet.
Real people don’t look like that! 😂
His brain…
😁LOL! You’re a puppet…yeah well you’re a puppet’s puppet!
He cuts his own hair with his mom’s sewing scissors. Little too much off the bangs this time, though.
I always thought he looked like Star Trek’s Data.
Absolutely. More so all the time. But why do it when you have enough money to look like a million dollars?
LaurenWitzkeDE
@LaurenWitzkeDE
20h
·
·
Edited
Joe lost Arizona, and when the truth comes out- We must settle for nothing less than the full criminalization of electronic voting machines and vote by mail.
Oh, and charging all those involved with treason.
https://nationalfile.com/arizona-state-senator-wendy-rogers-reports-from-maricopa-audit-floor-says-results-could-be-legally-actionable/
ARIZONA: State Senator Wendy Rogers Reports From Maricopa Audit Floor, Says Results Could Be ‘Legally Actionable’ – National File
Arizona State Sen Wendy Rogers toured the floor of the Maricopa County forensic audit on Thursday, confirming that the results could be “legally actionable”
National File
View Link Feed
1,837 likes
171 comments
763 reposts
I expect to see a lot more of this as things heat up this summer.
https://twitter.com/disclosetv/status/1398781059748225029
Hope you are correct.
So, magically Antifa and BLM are going to be arrested. Wonder if they will continue, Catch & Release”.
Till the bastards are locked and prosecuted, zero faith in Seattle /Portland PDs and DAs to enforce the law.
So, mini ground report.
I sang a Vigil Mass this evening. The Church itself sits…280ish…when full before people start standing around the perimeter. There were a good 75-80 people there, and many I haven’t seen in months. Most masks were off, and the people sang. Really sang. It was closer to normal then it has been in a long time. However, just about everyone is still distancing. I told the organist that distancing was a must with me. She was puzzled, but respected that I wanted to be beyond spitting distance.
The true believers in the shots just aren’t getting the message from their sources about the transfer, I’m convinced. They really think we’re nuts.
I know a couple of people named in this article, one I disliked a lot. But the one I disliked changed my thinking because he did a very good thing, for which I will always respect him. And the other I know (somewhat, but enough) surprised me also. I thought he was typical and purely political, but he was not. I was wrong.
This is a very moving article, and IMO a must read. Implicitly, it shows the evil of evil men, and the good of good men. It made me proud to be from Buffalo, although I have no personal connection to the matter.
Evil men worked hard to ensure that people died and suffered.
I generally do not like the cowardly and insensitive medical profession, but the good men proved their true humanity. There is a core of good men in every profession, who do what they wanted to do, and are what they wanted to be:
https://www.mountainhomemag.com/2021/05/01/356270/the-drug-that-cracked-covid
New video on Political Moonshine:
https://politicalmoonshine.com/2021/05/29/insurrection/
INSURRECTION?
May 29, 2021
VIDEO: Why does Nancy Pelosi’s House require a commission for the “Capitol insurrection”? Because it was a “organized event.”
Oh, that is an AWESOME video!!!
New article on Political Moonshine:
https://politicalmoonshine.com/2021/05/29/two-more-coffin-nails-and-100-certainty-of-covid-19-fraud-can-anyone-prove-it-isnt/
Two More Coffin Nails and 100% Certainty of COVID-19 Fraud – Can Anyone Prove It Isn’t?
May 29, 2021
Intro: “Care to understand how COVID-19 is a false flag political construct that was intentionally developed as a bio-WMD to facilitate the overthrow of the U.S.? Then this article is for you and it includes an abundance of links and other resources to verify positions and provide you with all of the evidence you need for a deeper and clearer understanding of what is being done to us. That’s right – done to us.
On a date conveniently saddled between Christmas and New Year’s Eve 2019, when the majority of the Western world was occupied and distracted with both holiday recovery and preparation, the world fundamentally changed on 27 Dec 19 when the SARS-CoV-2 outbreak (not yet a “pandemic”) was first announced in the mainstream media news. They eased it in and perhaps many missed it.
GETTING TO THE PRESENT DAY
Curiously and by means of evidence later provided to me by an epidemiologist, we confirmed that the U.S. and other Western nations were ordering “COVID”-specific test kits and supplies by a name that technically wouldn’t exist until 11 Feb 20, when the WHO/CDC cohort would officially apply the “COVID-19” moniker to it.
Moreover, the evidence demonstrates that the U.S. and those other nations were making such “COVID-19” purchases dating back to 2017 and in each and every year up to 2019. How does that happen outside of a planned event? It doesn’t – period.”
Both Lin Wood and Patrick Byrne have posted this article on their respective telegram channels today.
From OT:
Ivermectin, The Drug That Cracked COVID and Treated President Trump
May 29, 2021
SD: “Before going into a fascinating story about a drug called “Ivermectin” and a volume of research studies, successful trials and treatment for COVID-19, there is something to consider that should be forefront.
There is so much hype over the vaccines by all elements of big pharma, government and media; and there has been such widespread acceptance of the hype by millions of Americans who have taken the vaccine; it is important to consider how those invested people would react to any conversation about an inexpensive, safe and effective treatment now.
So many people have bought into the vaccine narrative, and so many people have exposed themselves to the risks of an untested, non-FDA approved experimental treatment, they simply will not be able to admit (or accept) any form of truth that runs counter to that narrative. To admit alternative safe treatments were the better option, is to admit you have been duped and exposed yourself to risk unnecessarily.
That said there is a remarkable, albeit long, article and story about a group of physicians who developed a COVID treatment protocol around the drug Ivermectin. The story is long, but well worth the read.”
Excerpt below:
Mountain Home Magazine
.
I dodn’t remember anything about DJT being treated with Ivermectin.
I specifically remember him saying he was treated with Regeneron.
https://www.regeneron.com/covid19
Yes – it was REGENERON – a synthetic antibody cocktail.
https://www.regencov.com/
Fun fact: “Dodn’t” is what happens when you decide to change didn’t to don’t and forget to remove the second ‘d’ 😁
But what happens when you decide to change it?
The embedded article says VSG took Ivermectin at Walter Reed, but that info was not released to public. So yes, he had both Ivermectin and the Fountain of Youth.
FLCCC.net Dr. Pierre Kory’s alliance with all the Ivermectin info, protocols and docs who will prescribe for treatment or prophylaxis. Hubby and I are both on it, I switched over after a year+ on HCQ.
Fort McHenry. America’s proving ground. Something’s up. (PS I LOVED the place when my family visited when we were kids.)
Possible connection between this tweet and the earlier “B” post on 8kun.
Thunderboomer brewing here, and I suspect it’s going to rain elephants and rhinos here. So here’s hoping the power stays up.
Ill take some of that rain!
You can have mine! It’s rained for 2 weeks straight here and more on deck for next week, Grr.
How’s the temp? Is Darwin going to be ok?
No issues with temperature this time.
Of course we *could* still have a snowstorm in early June. It has happened.
This is excellent:
[Exclusive Documentary] DeSantis: Florida vs. Lockdowns
[Exclusive Documentary] DeSantis: Florida vs. Lockdowns (theepochtimes.com)
Patrick Byrne’s book about the stealing of the election, The Deep Rig, has been made into a movie featuring Byrne and Gen. Flynn. It will be released on June 19th. The trailer can be seen here:
https://thedeeprig.movie
JovanHuttonPulitzer https://t.me/s/JovanHuttonPulitzer
WE THE PEOPLE: PATRIOTS DAY RALLY
WHEN: THIS SUNDAY ***MAY 30th***
FROM: 1:00PM – 6:00PM
WHERE: 18024 137TH TRAIL N, JUPITER, FL
If you are unable to attend in person, catch our LIVESTREAM here: https://www.clouthub.com/defendourunion
General Michael Flynn interview
The Right Side with Doug Billings Published May 28, 2021
The Right Side with Doug Billings – May 28, 2021 (rumble.com)
http://a.msn.com/09/en-us/BB1gfXGp?ocid=se
It’s does work! Click for a wonderful Simone Biles ad, with the Blue Danube Waltz. 👍🏻
I’m working my way through old posts from when on vacation. Thanks for your physics explanations, which tend to hover over my head, but w/ application of diminishing brain power could conceivably make sense. You are providing an heroic service & a nice break from all the CV insanity! Blessings!
If truly interested going back and hitting them again in a few weeks might make things clearer.
Yes, a refresher course when the time & inclination permit. Honestly until after my daughter’s wedding in 2 months that’s not very likely for me. Your reasoned explanations are very well done, it’s my own brain block that gets in the way 🙂
Geez if you’ve got a wedding in two months no wonder you can’t think straight.
LOL! Don’t discount the age factor or even how the pregnancy hormones (back in the day) destroyed/transformed A Lot of my cognitive “skills”…not to mention that I Failed calc-based physics twice (pridefully, shouldn’t have taken the harder course at the outset) in college before barely passing general physics (required for my pre-med major). Got just a bit of a mental block there it seems…