2021·05·22 Joe Biden Didn’t Win Daily Thread

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.

Not an Eagle

On my way to work there’s a large nest up in a half-dead tree, and I’ve been reminding myself to take pictures sometime. Well, I finally managed to do so and I established two things. 1) The autofocus on the camera I used sucks and 2) it’s not an eagle nest; it’s some sort of falcon with a white body. (The head is dark, even if it were an eagle it’d be a golden eagle, not a bald eagle.)

Postmodernism, a/k/a “Theory”

The other day I read a book review, regarding “Cynical Theories: How Activist Scholarship Made Everything about Race, Gender, and Why This Harms Everybody” by Helen Pluckrose and James Lindsay.

I must emphasize I have not read the book. According to the review, it doesn’t actually spend much time on many of the more politically noisome aspects of this latest version of “postmodernism,” but it is invaluable in going a step deeper in critiquing it than many others do.

A lot of the sheer nonsense pervading the Left is so crazy to anyone with a sane worldview that we find it hard to believe that the other side really believes this crap. But they do, because it is part and parcel of a nonsane worldview. And this broader worldview is discussed in the book. It makes Leftist nonsense seem at least somewhat sane within its own context.

We of course spend a lot of time here bashng “Critical Race Theory” (as it deserves) but other aspects of it are pernicious too and I thought I’d adapt the capsule summary of “Theory” I read in the review, here.

“Theory” apparently represents the latest wave of “postmodernism” which began in the 1960s with the work of Michel Foucalt. He argued that there is no such thing as objective truth. Or, if there is such a thing, it’s inaccessible to us because our knowledge is nothing but “narratives,” stories we tell each other and use to keep power.

Leaving aside the jokes playing off the fact that that statement itself is a claim to an objective truth, if there’s no such thing as objective truth, then basically anything goes.

Those two principles lie at the root of “Theory.” The next layer are four “attitudes” or methods.

the blurring of boundaries between intellectual and social categories. This can result in anything from men wearing dresses to scientists relying on anecdotes.
An emphasis on language as the tool that controls every aspect of life.
Cultural relativism–not just in morality (e.g., cultures where behaviors we consider corrupt are considered normal, for instance) but even in epistemology. In other words the methods we use for figuring out the world around us are only valid in our culture. Some other culture can adopt other rules for determining, say, if gravity works.
The lack of distinction between the individual and the universal. This means, among many other things, that “truths” (they insist on a plural there) have meaning only for a group. There aren’t any Steve truths, there are White Male truths. But there also isn’t a truth that is true for all of mankind either.

That’s the philosophic underpinning of today’s Left. No wonder they’ll believe such silly things.

It’s hard to predict what, exactly, the postmodernists will actually do with this, because as I said, these rules mean there are no rules for determining what is and isn’t true, much less what to do about a fact once it’s discovered. The PoMos themselves use bizarre jargon and revel in being incoherent. It’s a feature not a bug. And that’s a consequence of their basic beliefs. There’s no truth, “logic” is just one of many “ways of knowing” and one which must be tainted by racial/sexual/class bias…so what need to express oneself clearly or to give actual proof of one’s assertions?

Demanding that they be lucid is seen by them as a form of oppression; we’re trying to force them to use our standards.

Remember back in 1996 when Alan Sokal (a physicist) wrote a paper full of gibberish and it got accepted by a PoMo philosophy journal? The authors of this book repeated that in 2018, with over a dozen BS papers. One of those papers rephrased Mein Kampf in feminist jargon!

Cynical Theories makes the case that this stuff was apparently harmless up until the 1980s. The practitioners were unable to articulate an ideology, and couldn’t, therefore push to influence society. But in the 1990s they shifted gears. Keeping the two principles and four methods above, they fashioned a menu of separate specialist theories, e.g., “postcolonial,” “queer” and our current favorite, “critical race theory” among them, aimed at “deconstructing” things society used to take for granted, to show there was no objective truth there but just an attempt to hold power and oppress minorities. An example given in the review is “Disability and fat studies.” According to this even deaf or paralyzed people don’t suffer from their disabilities but rather from prejudice against them, held down by the network of power relations in society. So they argue that disabilities are yet another kind of “identity” and that trying to alleviate deafness or paralysis is actually oppressive and exploitative. And if a deaf or paralyzed person asks for help, he’s internalizing his own oppression.

Around about 2010 this garbage heap of “theories” coalesced into “Theory.” Collectivism is merged with the rejection of objectivity and now we have statements like “There’s no true truth but there are different truths for different categories of people.” Pluckrose and Lindsay explain “Having oppressed identities gives the oppressed a richer, more accurate view of reality-=hence we should listen to and believe their accounts of it.”

The dominant society, meaning, you guessed it, white male society, commits injustice against these groups when it fails to affirm their beliefs.

This is an inversion of Marxism, which claimed that the oppressed workers suffer from “false consciousness.” Now it’s the (alleged) oppressors who suffer from it, because they’ve been socialized to believe a certain set of “truths” that benefits them.

Special attention should be paid to the premise that language effectively constitutes reality, and blinds the majority to the fact that they are oppressing the minority. This accounts for one of the most aggravating aspects of the Left: They will insist on orthodoxy while simultaneously disowning their own efforts to enforce it.

And of course, this is why they conflate speech with violence. Because in their view, speech isn’t about reality, it is reality. A difference of opinion creates a power imbalance that threatens to erase a person’s only source of significance, which is other people “affirming” their “experience.” To listen, therefore, requires not just listening but actually affirming. Disagreement or criticism are inherently unjust.

There’s more, much more…I will probably be buying the book.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.

(Hmm a few extras seem to have crept in.)

Spot Prices

All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend).

Last week:

Gold $1844.90
Silver $27.53
Platinum $1232.00
Palladium $2949.00
Rhodium $27,600.00

This week, markets closed for the weekend at 3:00 PM Mountain Time

Gold $1880.70
Silver $27.63
Platinum $1172.00
Palladium $2834.00
Rhodium $25,500.00

Gold is doing very well. Platinum took a big hit, palladium fell 76 bucks on Friday alone, it’s now far away from its $3000+ dollar high point.. Rhodium is down, too, $1200 on Friday alone. Perhaps the PGM bubble is bursting? Realistically, it’s too early to tell.

Electricity and Magnetism (First Half)
(Part IV of a Long Series)

Introduction

The general outline of this story is to start off by putting you “in touch” with the state of physics at the beginning of 1895. Physicists were feeling pretty confident that they understood most everything. Sure there were a few loose ends, but they were just loose ends.

1895 marks the year when people began tugging at the loose ends and things unraveled a bit. In the next three years, three major discoveries made it plain there was still a lot to learn at the fundamental level.

Once I’m there I will concentrate on a very, very small object…that ties in with stars, arguably the biggest objects there are (galaxies are basically collections of stars). And we would never have seen this but for those discoveries in the 1890s.

It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.

And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it…but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)

Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I used 9.8 kg m/s² last time for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.

A couple of go-backs.

I’m actually used to dealing with newtons, joules, and watts as abbreviations, N, J and W. Of course now I’m writing for an audience of about six people many of whom haven’t taken the same classes I have, and often spelling the units out. Ignorantly, I’ve capitalized them because their abbreviations are capitalized. That was wrong. Although the names of the people the units are named after are, of course, capitalized, the units themselves should not be. I knew this 40 years ago, I forgot. For example, “The metric unit of power, the watt (W), was named after James Watt.”

I beg your pardon for this error.

More substantively, I thought I’d say a bit more about the dot product.

And this time, I will reference trigonometry. Just a teeny bit. This won’t hurt…much.

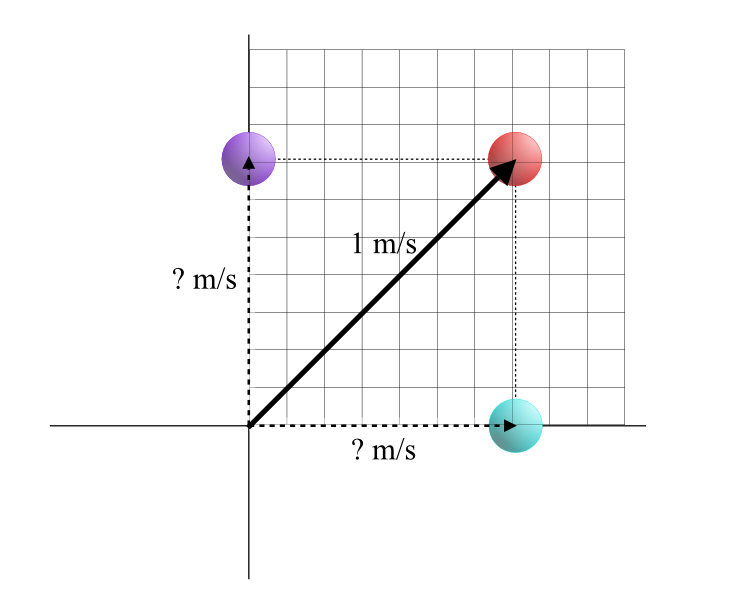
Pictorially, a dot product of two vectors is equal to the magnitude of the perpendicular projection of one vector onto the other, times the magnitude of that other vector.

OK, that’s a mouthful! Let’s call our two vectors A and B. Last time around we defined a symbol for the magnitude of a vector, so that the magnitude of A is ∥A∥ and the magnitude of B is ∥B∥. But let’s also make one more convention, let a_b be the magnitude of the projection of a onto b, and let b_a be the magnitude of the projection of b onto a.

So a dot product of A and B is equal to a_b∥B∥. But it works the other way, too, A•B = b_a∥A∥.

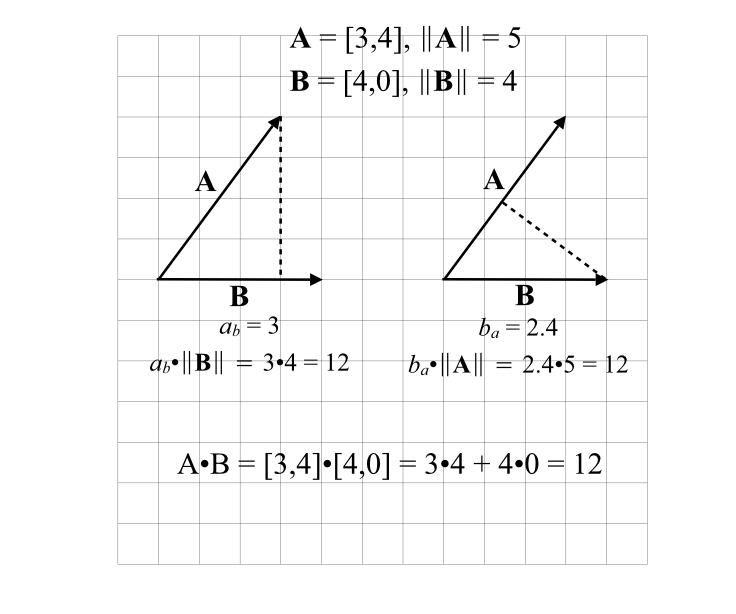
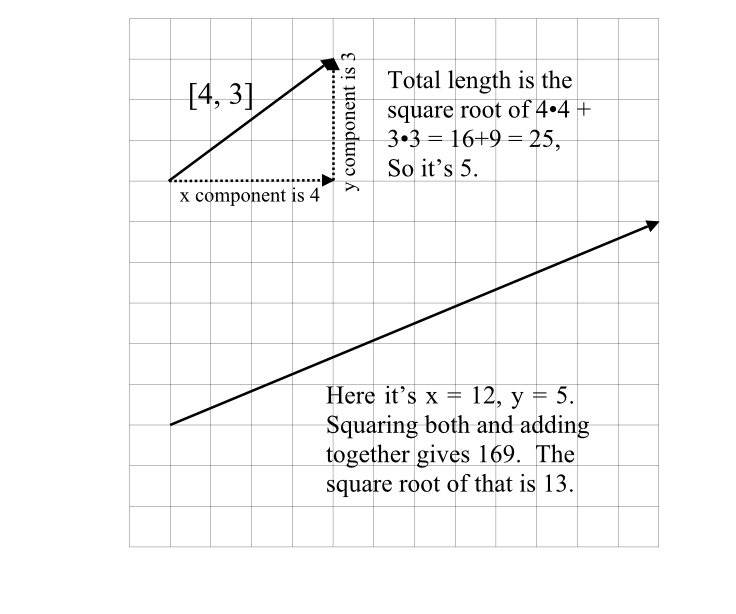
Figure 4-1, graphical interpretation of the dot product.

If you drop a line from the end of A to B, so that that line hits B perpendicularly, you’re said to have projected A onto B. In this case, the length of A‘s projection onto B is a_b=3.

But you can also project B onto A, as in the second part of the diagram. When you do that, the length of the projection, b_a is 2.4. I didn’t measure that, but I used ratios. The length of A is 5 (it’s part of a 3:4:5 right triangle), and the length of B is very obviously 4. The two triangles formed by the vectors and the dashed “dropped” line are similar, they share one angle where the two vectors meet, and a right angle, so all of the angles have to be the same. So if the hypotenuse of one is 5, while the other is 4, the other two sides must also both be cut by 20 percent. The projection of B onto A must therefore be 20% less in length than the projection of A onto B (which we know is 3), so that length must be 2.4.

In the left hand diagram, “the magnitude of the perpendicular projection of one vector [A] onto the other [B]” is 3. The “magnitude of that other vector [B]” is 4. The product is 12.

In the right hand diagram, these numbers are 2.4 and 5, respectively. The product of these two is also 12.

The dot product of these vectors is: [3, 4]•[4,0] = 3•4+4•0 = 12+0 = 12. So it works, at least in this example. I’ll let you look up the proof; I’ve only told you what it means.

What if both vectors are unit vectors? Since the vectors are of exactly the same length, their projections onto each other are the same, and since the vectors are of length one, the lengths of their projection onto each other will be one (if they are pointing in the same direction), or -1 (if they are pointing in opposite directions) or some number in between.

That number is the cosine of the angle between them, abbreviated cos.

The usual way of teaching trigonometry, shown in the first part of figure 2, involves drawing a “unit circle” (one with a radius of one), sticking this circle onto a Cartesian grid, and then drawing a line at some angle from the center of the circle to a point on the circle. Obviously the coordinates of that last point are going to differ depending on the angle, but the x value is the cosine, and the y value is the sine, abbreviated sin.

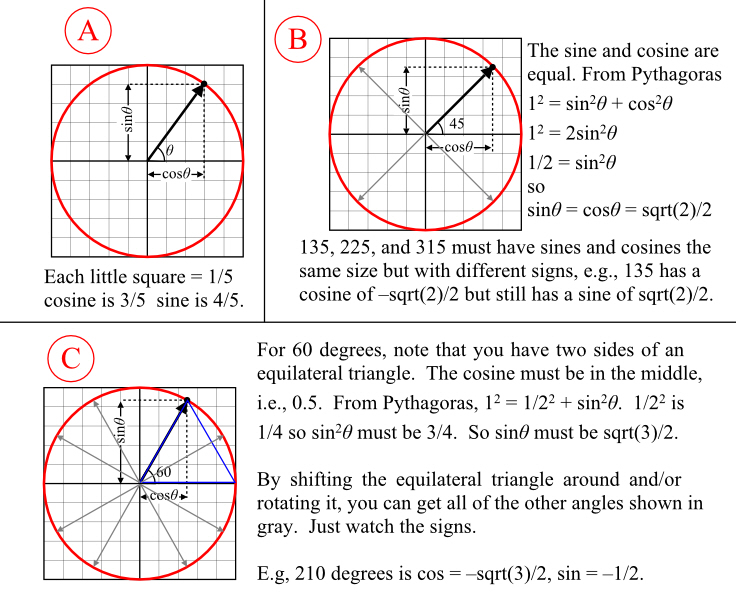
Figure 4-2 A capsule lesson on Trig, from the first day of class.

But you can look at the cosine of the angle as being the same thing as the projection of a unit vector onto a unit vector lying along the x axis.

Go back to my prior statement, about what a dot product was:

Pictorially, a dot product of two vectors is equal to the magnitude of the perpendicular projection of one vector onto the other, times the magnitude of that other vector.

With a pair of unit vectors being “dotted” together, both magnitudes in that sentence are 1. So, for unit vectors, it’s equivalent to

“a dot product of two unit vectors is equal to the magnitude of the perpendicular projection of one vector onto the other.”

But we just saw that the projection of one unit vector onto the other is the cosine of the angle between them. So if both vectors are unit vectors, the dot product of those vectors is the cosine of the angle between them.

If the first vector is not a unit vector, but is, say, twice as long then the magnitude of its projection onto the other is simply twice as long as well. In other words, that projection length is the magnitude of the vector, times the cosine of that angle.

You can go back to the original statement. The dot product of two vectors is the cosine of the angle between the vectors, times the magnitude of the first vector, times the magnitude of the second vector.

So the formal definition of a dot product is:

A•B = ∥A∥∥B∥cosθ

where θ is the angle between the two vectors.

This gives you a sneaky way to figure out the angle between two vectors. Take their dot product. Then divide by the magnitude of the first vector, and divide again by the magnitude of the second vector. You now have the cosine of the angle between them. You can look up the “inverse cosine” (i.e., the reverse of taking the cosine). Today, you can use a calculator (or calculator app). A few decades ago, a fancy slide rule might have a scale on it for cosines, from there you can look up the angle. Also you could look it up in a table. Sines and cosines are actually very well known functions.

There are a number of angles with well-known cosines that are actually expressable as somewhat-sane numbers. 45 degrees, for instance, is an angle at which the sine and cosine are equal, (see part B of figure 2). You can draw a right isosceles triangle there, which means the two legs are equal. Using Pythagoras, c² = b² + a² for right triangles (with c being the side opposite of the right angle), and knowing that c = 1, and a = b, 1 = 2a². So a² = 1/2. Now a is equal to the cosine, or the sine in this case, so both are equal to the square root of 1/2, sqrt(1/2) (sorry, I can’t do fancy square root signs here). That’s 1/sqrt(2), but mathematicians hate it when you put a radical in the denominator, so they multiply top and bottom by sqrt(2) and get sqrt(2)/2. This is roughly 0.707. Similar reasoning will get you the sines and cosines of 135, 225, and 315 degrees, you’ll have to put negative signs in as appropriate.

60 and 30 degrees are other convenient angles. For instance with 60, you can get the answer from realizing that you can draw an equilateral triangle here, as shown in part 3. The X line, the slanted line, and a third line are all length one, and that’s a 60 degree angle there. It’s a symmetrical triangle, so the cosine has to be 1/2. The sine can be had from Pythagoras, too: sqrt( 1 – (1/2)²) = sqrt( 3/4 ) = sqrt(3)/2. Sqrt(3) = 1.732 (remember, Washington’s birth year), sqrt(3)/2 = roughly 0.866.

You can use similar reasoning for 30, 120, 150, 210, 240, 300, and 330 degrees.

Thes are all “magic angles” (as I called them last week) because you just know the sine and cosine and in some cases it’s even a nice nifty fraction like 1/2.

Most angles in whole degrees give you absolutely ugly sines and cosines.

OK, with that exceedingly gentle intro to trigonometry and the additional info on dot products out of the way…

Electricity

It has been known since at least 600 BC that amber (fossilized tree sap), when rubbed, could attract light objects. This was noted by Thales of Miletus. (There is no extant record on whether Thales had difficulty with the sheets coming out of his clothes dryer.)

Sometime in the next 2000 years, someone noticed that glass exhibited the same behavior.

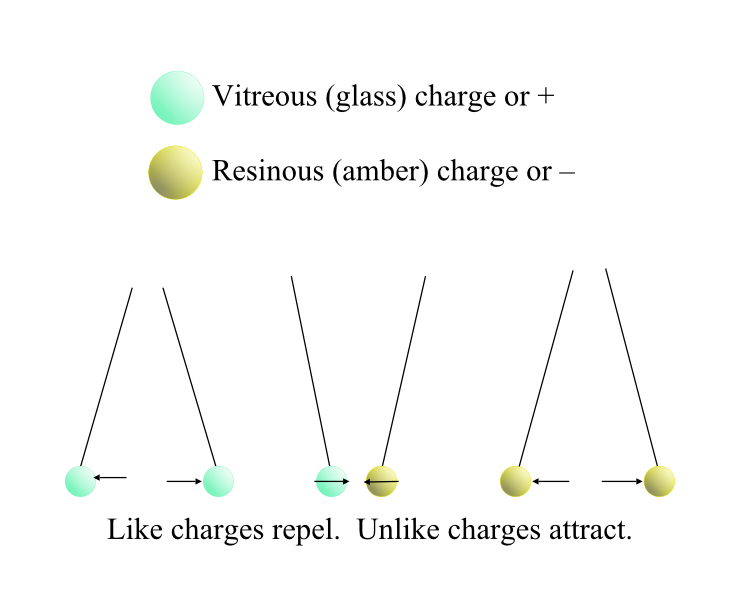
In 1723 Charles Francois Du Fay, a French physicist, realized that actually, glass and amber didn’t quite behave exactly the same way. Whatever it was they were doing was different in a rather interesting way.

Suspend two corks on silk threads. Buff up a piece of amber, touch one of the silk threads. The two corks are attracted to each other, somewhat. Buff up the piece of amber again, and touch the other silk thread. Now the corks actually repel each other, somewhat more strongly.

Whatever it is that’s in the amber that makes it attract small objects, when introduced to two different objects, caused them to repel each other, as if the whatever-it-is repels itself.

Repeat this experiment, but this time touch the second thread with a rubbed bit of glass. Now the two corks attract strongly. And if you repeat again, and touch both threads with the bit of rubbed glass, the corks repel each other again.

There is, in other word a resinous electricity (from amber) and a vitreous electricity, from glass, and they appear to be two different things, but able to interact with each other.

So vitreous electricity repels itself, but attracts resinous electricity (and vice versa), and resinous electricity repels itself too. They both seem to attract small things that don’t have any electricity in them at all. Like repels like and attracts the other.

Figure 4-3 The basic rules of Du Fey’s two electrical fluids.

At this point Du Fay came up with a fluid theory of electricity. Each kind of electricity was a different sort of fluid that would flow from solid object to solid object.

In the 1740s an otherwise obscure individual by the name of Benjamin Franklin in Pennsylvania did some more work. He was able to show that if you took an object with one of the two kinds of charge, and touched it with an object of the other kind, the charges disappeared, as if they had cancelled each other out.

Franklin came up with the single fluid theory. In this one electricity was a sort of fluid and under ordinary circumstances, an object would have a certain normal amount of it. But when it was in surplus, you saw one kind of charge, when it was in deficit, you saw the other kind. (In very similar fashion, surplus money can be used to pay off debt, a negative amount of money.)

And indeed this analogy suggests that the charge with the surplus of fluid could be considered positive, and the charge from a deficit of fluid could be called negative. This would be mathematically convenient. It wasn’t meant in any sort of pejorative way.

That is precisely what Franklin chose to do. However, he had no idea which kind was the surplus! He labeled the vitreous charge “positive” and the resinous charge “negative” and it has been this way ever since. His chances of getting it right (assuming a fluid was moving) were 50-50.

The charges could just as easily have been labeled black and white or red and green or yin and yang. But by Franklin’s time mathematical rigor had begun to pervade science, and so positive and negative, they were.

One difficulty with Franklin’s theory was that although one could imagine a fluid repelling itself (like two positive charges would do), but it was more difficult to imagine the lack of such a fluid in two objects creating a repelling force. Nonetheless, Franklin’s formulation was a lot more widely accepted than Du Fey’s.

One can also have different strengths of charges; one piece of rubbed glass might have twice as strong a charge as another. That, presumably, meant the first had twice as much of the fluid in it as did the second. Similarly, pieces of amber could have different deficits of the fluid. In order for charges to completely cancel out, it turns out, they must have equal magnitude but be opposite. If one is of greater magnitude than the other, then the result of the cancellation will be a slight amount of that charge, the leftover part that couldn’t be cancelled out by the other.

Imagine coming up with some way to measure charge, and you have a positive 3000 charge and another negative 2800 charge. Putting the two together, you’re left with a positive 200 electric charge, just like you’d get from adding the numbers +3000 and -2800.

There is in fact a unit of electric charge, the coulomb, named after Charles A. de Coulomb, and it seems to be a very large unit.

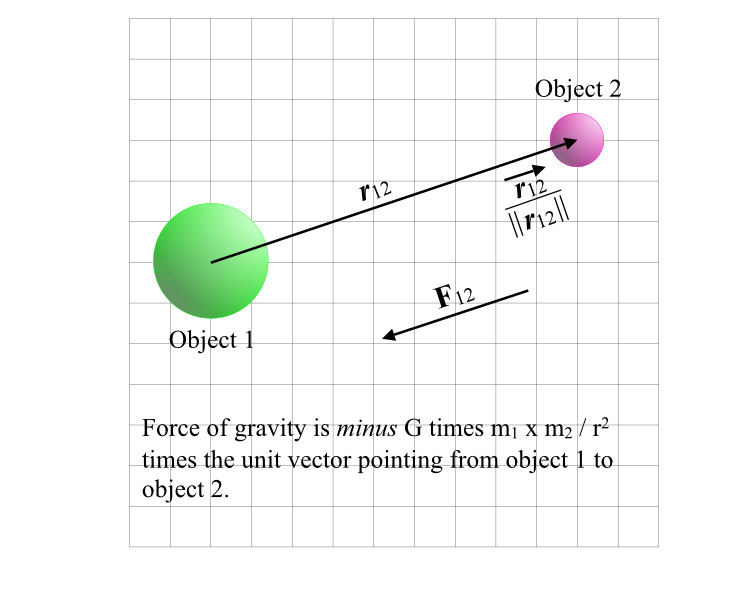
Who was Coulomb? He formulated the law of force between electric charges. This law superficially resembles Newton’s law of gravity. F₁₂ is the force exerted by charge 1 on charge 2.

F₁₂ = (kq₁q₂ / r²)•ȓ₁₂.

As a reminder Newton’s law of gravity was

F₁₂ = -(Gm₁m₂/r²)•ȓ₁₂.

So instead of the masses, we have q, the electric charge of the objects, and we have a different constant, k. G was a small number, 6.67 x 10^-11, indicating that two one kilogram masses a meter apart would attract each other with a force of 6 trillionths of a Newton.

The k in Coulomb’s law is 8.99 x 10⁹. In other words, nine billion.

So two one Colomb charges a meter apart act upon each other with a force of nine billion Newtons. Which is almost the weight of a billion kilograms on earth, or about a million English-system tons. From one Coulomb acting on another.

As I said a Coulomb is a huge unit! The sheets in your dryer don’t stick to each other quite that hard, but when you remember static electricity can lift small objects against gravity, it’s pretty plain the electric force is likely inherently stronger than gravity.

Although Coulomb’s Law and Newton’s law of universal gravitation look a lot alike, with charge and mass filling in for each other, and different fudge factors, there’s one very important difference.

Newton’s law has a minus sign in it. Coulomb’s law does not. The minus sign serves to make gravity an attractive force, because it makes the force vector point the opposite way as the displacement unit vector. This doesn’t happen with electric charges.

But don’t we have situations where electric charges attract? Sure we do. And even though this formula describes a repulsive force, it does allow for this, because the result is negative when some part of the formula is negative; r² must be positive, k is positive, so the only way that can be is if q₁q₂ is negative. If both charges are positive, the product is positive…and they will repel. If one is positive and the other negative, the product is negative, and it’s like gravity; they attract. Finally if both charges are negative the product is positive, and the two charges again repel each other.

So that’s how charges behave. It’s oddly like gravity and also oddly unlike gravity. And it’s a lot stronger than gravity.

Conservation of Electric Charge

It eventually became evident that electric charge is conserved. If your system starts out with 0 total, in other words, “electrically neutral,” you can create a charge somewhere in it, but always at the cost of creating an opposite charge somewhere else in the system–again, as if some amount of fluid had moved from one place to another. And if there is a charge somewhere in the system, it can only disappear if it’s combined with the opposite charge from somewhere else in the system.

What of the small objects…dog fur, scraps of paper, and so on, that are attracted to an electric charge, even though they’re neutral? For example, imagine dog hair stuck to positively charged glass.

We know the dog hair is not simply charged the other way. negatively, because it’s attracted to both kinds of charge.

As it turns out the electric fluid in the dog hair–it has some in it, just exactly enough to be neutral–is repelled by the glass’s positive charge, and ends up at the far end of the hair. Of course, this means the end of the hair closest to the glass now has a negative charge. And the negatively charged end is closer to the glass than the positively charged end is, so the attractive force is stronger than the repulsive force. Voila! The (overall) neutral object now sticks to the positive charge. Even if the hair is lying flat against the glass (and it probably is), the side touching the glass is closer than the side far away.

For the most part, the phenomena we’ve been talking about involves static electricity, electricity that is not moving. Sure, one of our experiments involved having it move along a silk thread. And there were also Leyden jars which could hold a substantial charge and would release it when the contacts were touched—sometimes enough charge to knock a man down. But for the most part, the charges didn’t move.

But electricity is much, much MUCH more interesting when it is moving, especially either steadily or in an oscillating fashion! More on that later; I have to set this aside and start another “thread” of thought now.

Magnetism

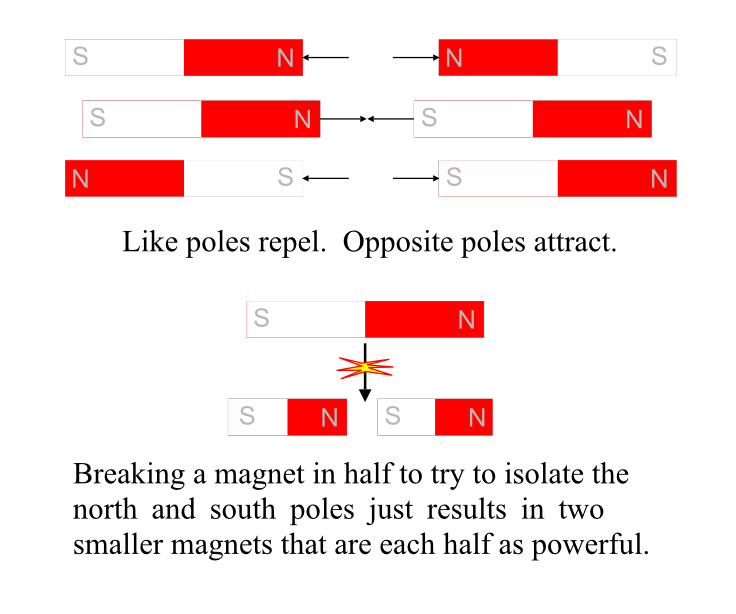
Another phenomenon, very similar to electricity in some ways and rather different in others, also turned up in ancient times. There were occasional rocks that would attract iron. They would also attract each other. But sometimes they repelled each other. And it turned out that the SAME rock would have a part that would repel the other rock, and one that would attract it. On the other hand, this didn’t matter when the rock was interacting with iron; either end would attract it.

This, of course, is what we now know as magnetism. And those two ends that attract or repel each other became known as poles.

That’s because a magnet, left free to swivel, will always point one of its two poles roughly toward the Earth’s north pole, that’s called the north pole of the magnet. The other is the south pole of the magnet. When it becomes a matter of representing these things mathematically, the north pole is considered “positive.”

Very much like electricity, similar poles repel, opposite poles attract. (Ironically, this means the Earth must be a giant magnet, with that magnet’s south pole near the north (geographic) pole, so it can attract magnets’ north poles.)

What happens if you break a magnet in half to try to separate the north pole from the south pole? You get two smaller, weaker magnets, each with north and south poles. The broken end of the north side of the old magnet is now a south pole, and the other side of the break is now the north pole of the other new magnet.

In fact, no matter how small you break a magnet, you will never succeed in having just one pole. This sort of thing, if it existed, would be called a “magnetic monopole” and it’s a true unicorn.

Magnets, too attract or repel each other in inverse propotion to the square of how far apart they are–which is mathematician speech for “there’s an r² in the denominator.” This is hard to see or even use, though, because there’s always an opposite pole nearby which partially cancels things out.

Magnetic poles didn’t seem to move around within objects like electric charge does. But there was a sort of conservation law; in breaking a magnet in two, you still had equal numbers of north and south poles And the fact that there are no monopoles tells you that the total amount of “north pole” must be equal to the total amount of “south pole” because they always come in pairs.

Magnets, too, can be much more interesting when they’re moving.

Electricity Moving. Work and Potential

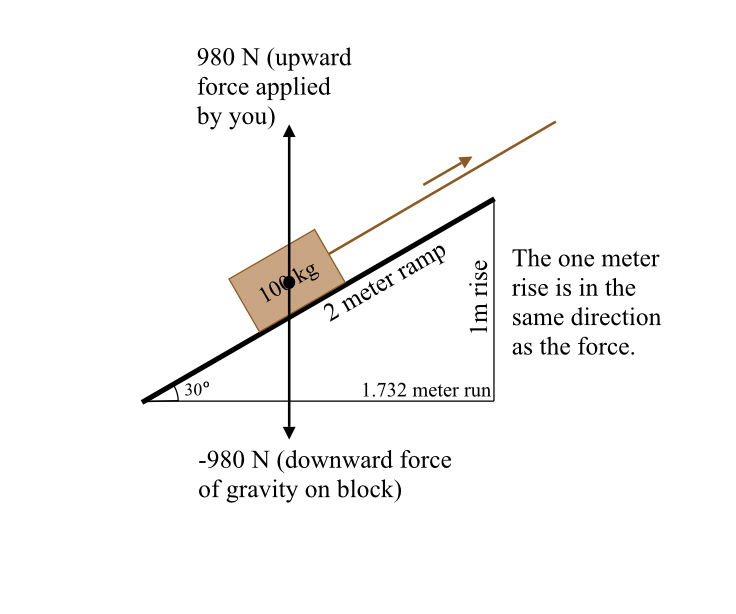
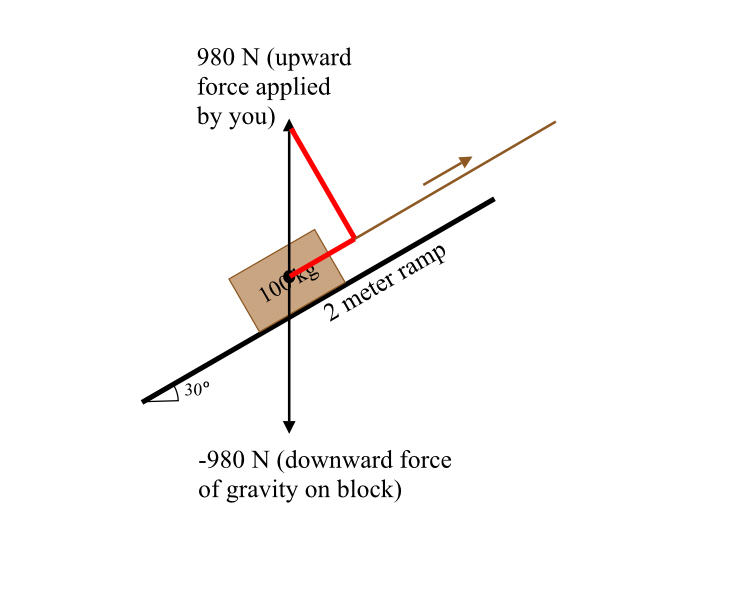
If there is a force, then work can be done.

Imagine an object, a kilogram in mass, with a coulomb of positive charge on it. Allow it the freedom to move. Put a fixed charge nearby, on an object that cannot move.

If you space things properly, that charged object will start to accelerate, at 1 meter per second per second. As if one newton of force were being applied to it.

That’s because there is a newton of force being applied to it, a newton of electrical force, not gravitational force, and not a solid thwack administered by an experimenter. And after a meter of this, the electrical force has done one joule of work, just like with every other kind of force.

In fact, you can draw an analogy here between the sort of potential we talked about, where the height of a cliff was related to how much work gravity would do on an object dropped off of it, to what the electrical force does to a charged object.

If, going from point A to point B, a coulomb charge has a joule of work done to it, the electrical (not gravitational) potential between A and B is one volt. Yes, that volt. Named after Allesandro Volta, about whom, more in a bit, and abbreviated with a capital V.

So the equation here is work = potential x charge. Double the potential, double the work; double the charge, double the work. Or 1J = 1V x 1C.

Equivalently 1V = 1J/C.

And similar to gravitational potential where twice as much work gets done by doubling the mass, you can get twice as much work out of a one volt potential, by having it operate on two coulombs.

Didn’t we just see that a coulomb is a gigantic charge? Or at least, that it exerts a very strong force, so big that no doubt we’ve never seen a coulomb out in the real world? What dang use is a volt? It must be pretty tiny to get only one joule out of a coulomb!

The fact of the matter is, though, that when electricity moves, a coulomb isn’t all that much, particularly if you can get it to move for a prolonged period of time.

This was quite a bit different from the static electricity games that people had been playing up to now. Sure, you could occasionally get static electricity to move (if not careful, it would move through you), but it would usually just do it all at once, and once it had moved there were no positive or negative charges. It was moving from a high voltage to a low voltage, all at once. Sort of like dropping a rock (hopefully not on your foot). Once the rock is at the bottom, you’re done getting work out of the system, and you’re done quite quickly.

Imagine, though, turning on a faucet and getting a continual stream of mass to fall. (Or imagine a waterfall.)

We figured out how to do this in the very late 1700s. The story starts with an Italian named Galvani in the late 1700s; he was dissecting frogs and noticed that a spark could make the leg muscles twitch, even though the frog was quite thoroughly dead. Then he noticed that if he touched it with two different metals, he could also make it twitch.

That was the clue that Allesandro Volta (1745-1827) needed. In 1799 he created something we now call a “voltaic pile.” Start with a disk of copper. Place on top of it a disk of cardboard soaked in salt water. Place on top of that a disk of zinc.

Run a metal wire from the copper plate to the zinc plate, and electricity will flow through it from the copper to the zinc. There’s clearly a “push” being given to the electrical fluid in the wire. That push is a potential of about 3/4 of a volt, but Allesandro Volta certainly didn’t call it that.

If you stack these, you can build up higher and higher voltages. Place another copper disk directly on the zinc one, another bit of salt-water-cardboard, another zinc disk, and the total is 1.5 volts. Do it again, and now you have 2.25 volts. And so on. As long as you put negative zinc right next to positive copper in your stack of these sandwiches, you build up voltage.

But the big thing is, electricity could now be generated chemically, and not just rubbing things together, and it was sustained for some period of time until this pile, what we now call a battery, ran down.

In just a few years, ending in 1808, Sir Humphry Davy was able to reverse things; instead of chemistry making electricity, he got electricity to do chemistry. He was able to isolate no less than seven elements from compounds that had previously proven to be too tightly bound to be broken by conventional chemical means. Up til then we were reasonably confident those elements were there; we just couldn’t actually prove it beyond a shadow of a doubt by getting those elements out of their compounds.

And as early as 1800 electricity from a voltaic pile was used to break down water into hydrogen and oxygen.

The thicker the wire, the faster the battery would run down. Almost as if more electrical fluid could “fit” in a thicker wire.

And now we have hit the concept of electric current. How much electricity is moving? That’s how much electric current there is.

One ampere is one coulomb flowing past a point, every second. It was named after Andre Marie Ampere (1775-1836). He did a lot of the early work on what he called “electrodynamics.”

If you look in your breaker box, you’ll likely see a lot of switches labeled 12, 15, 20 or even more “A”. That’s amperes, and when one of those breakers flips, you’ve drawn more than that many amperes through that switch. In a circuit whose breaker is labeled 12, twelve coulombs will pass through that breaker every second.

With all those coulombs moving around why hasn’t your house blown apart (or been sucked into a vortex) from all those coulombs attracting or repelling each other?

Because the electrical fluid moves, and it doesn’t accumulate anywhere. A coulomb flows from one side of the breaker to the other, but another coulomb of fluid is right behind it, so there’s no deficit to create a resinous/negative charge. And the fluid downstream from your breaker also moved on, leaving space for the coulomb that just flowed through the breaker. No accumulation, no net positive charge (and no places low on fluid to have a negative charge).

The wire forms a closed loop, with your house at one end, and a power source on the other, something that creates an electrical potential, so that current will flow from high to low. (This is sometimes called Electromotive Force, or EMF, and abbreviated with a script capital E: ℰ.)

In a battery the current is “pushed” by the battery through the wire, through whatever it is you’re using the electricity to operate, and back along another wire to the battery…which uses chemical energy to do work, and give it another push around the loop. So a battery converts chemical energy to electrical energy. Once it runs out of chemicals it can react, it’s dead. (This is another aspect of the conservation of energy.)

One difference between a battery and your house wiring is that in your house wiring the current switches direction, back and forth, sixty times a second (50 in Europe and some other parts of the world). This is called “alternating current.” A battery doesn’t switch back and forth, and it’s called “direct current.”

Digression

OK, I’m going to shift for a moment from physics to the metric system itself.

The newton, joule and watt are called “derived units.” They come from combinations of other, more fundamental units, the meter, the kilogram, and the second. Length, mass, and duration are very different things from each other, but force, for instance, has to do with mass, length and duration. But when it comes to electricity, we have yet another thing that’s different from everything else. So something having to do with electricity should be a fundamental unit. The metric system has seven fundamental units; we’ll probably only touch only two of the remaining three.

You would think that the fundamental unit for electrical things would be electric charge, but you’d actually be wrong. The “fundamental unit” having to do with electricity in the metric system is the ampere. The coulomb is defined as one ampere, flowing for one second (C = A•s); the volt is then defined as I stated above.

But it’s even a bit crazier than that. There are two metric systems! The one I’ve used all along is MKS, for “meter kilogram second” because that’s what it derives other units from. But there is an older, mostly disused system called “CGS” for “centimeter gram second,” it derives its unit of force, and energy and so on from centimeters, grams and seconds. Its unit of force is called the dyne—1 g cm/s². When you consider that the gram is 1/1000th of a kilogram, and a centimeter is 1/100th of a meter, it should be no surprise that the dyne is 1/100,000 of a newton. The unit of energy is called the erg, and it is 1/10,000,000 of a joule. These are tiny, tiny units. The MKS units are easily “felt” by people: who hasn’t lifted 100 grams (weighing about one newton) about a meter and done a joule of work? But that’s ten million ergs!

Returning to Electricity…

OK, back to the main story.

Returning to our electrical circuit, from battery positive terminal through something that uses the electricity for energy, then back to the negative terminal of the battery, current is flowing.

What if there is a break in the wire? Won’t the electricity simply pile up?

Only the slightest, tiny bit. As more electrical fluid goes down the wire an unbalanced positive charge builds up, it begins to repel the fluid headed its way and forces it to a stop. This happens very quickly, effectlively, the current just comes to a screeching halt the instant the break happens. And if you measure the potential across both ends of the break, it’s now equal to the potential of the battery, whereas before the break, there was no potential difference at that point, but current was flowing through it.

Electricity is very eager to move, at least in good conductors; it really hates piling up, because a pile of it is a bunch of the same charge confined to a small space, and every bit of that repels every other bit, and hard.

Is there any constraint on how much current flows? Certainly. Every material, even a wire, has a resistivity to the flow of electricity. The more resistance, the less current will flow for the same voltage. On the other hand, if you double the voltage, that’s double the push, and twice as much current will flow through that same object. This works pretty consistently (until you reach the absolute carrying “ampacity” of the stuff and it heats up and melts or vaporizes, at which point, you’re done with that bit). Given a volt put across two opposite sides of a cube of the stuff, how much current will flow? Given that number, you can figure out how much resistance a certain object will have. It increases with length, and decreases with cross-section, so you can figure out the resistance of a wire, or any other object you want to carry a current, if you know the resistivity of the stuff it’s made of.

If the object the current is trying to flow through allows one amp through when it’s subjected to a volt, it has a resistance of one ohm, named after Georg Simon Ohm, who figured out that current flow was proportional to the applied voltage, and the proportion was different for every kind of material. In fact, it’s a law: the current through an object is equal to the voltage across the object, divided by the resistance.

I = E/R

I is current, don’t ask me why. E is from “Electromotive Force” and R is…wait for it…the resistance. Or to put it in metric units,

1 A = 1V/Ω

That funky symbol at the end is a capital Greek letter omega (as in “alpha and omega”), and perhaps it was selected to be the symbol for the derived unit ohm, as a sort of pun (ohm-ega).

If you have a circuit, from the positive end of a battery through three different resistances and back to the battery, you can measure the voltage across those three items and they will all have a pro-rata share of the voltage the battery is supplying. Say, for instance, it’s a 12V battery, and you have three lights hooked up to it, each light is 100 ohms. They’re all equal, and so the voltage across each light will be 4V.

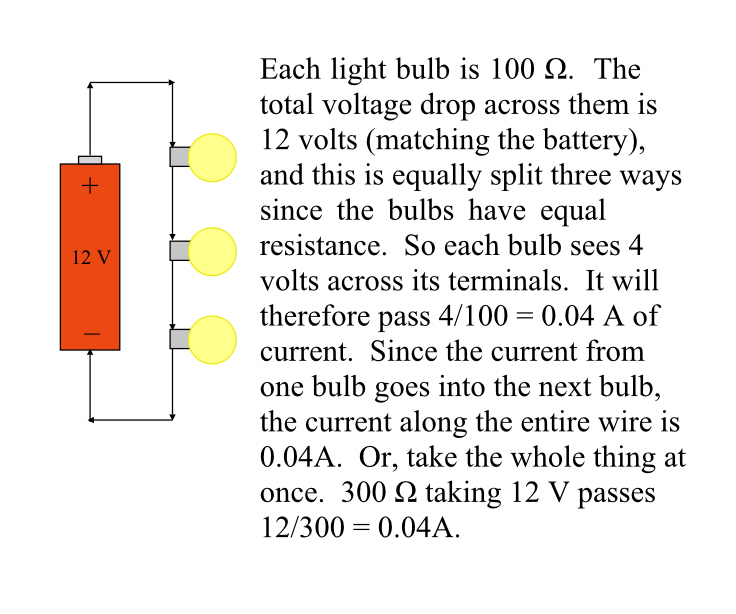
The current through any one of these lights will be 4V/100 ohms, or 0.04A. The same current goes first through one light, then the second, then the last, so it’s a good thing all of those currents are the same (or current would be coming in from nowhere).

By the way, on diagrams like this, for educational purposes, the wires are assumed to have zero resistance. So the voltage drop from the battery to the top terminal of the bulbs is E=IR = 0.4A • 0Ω = 0V. Likewise the wire between the bulbs has zero voltage drop.

Stringing a load end to end like that is known as wiring in series and usually is a stupid way to do things. (If one bulb blows out the circuit is broken and none of them work. Also, adding more bulbs increases the total resistance, reducing the current, and the total amount of light is actually less.)

Connect each of the three bulbs directly to the battery at both ends. This is parallel, because it splits the current into three separate streams. Each bulb now has 12 V across it, not 4, and the current through each bulb is 0.12A. Since each bulb gets a separate stream of current, the currents add up (instead of the voltages) and the battery is delivering 0.36A. Adding more bulbs adds more light, they each continue to use the same current as before.

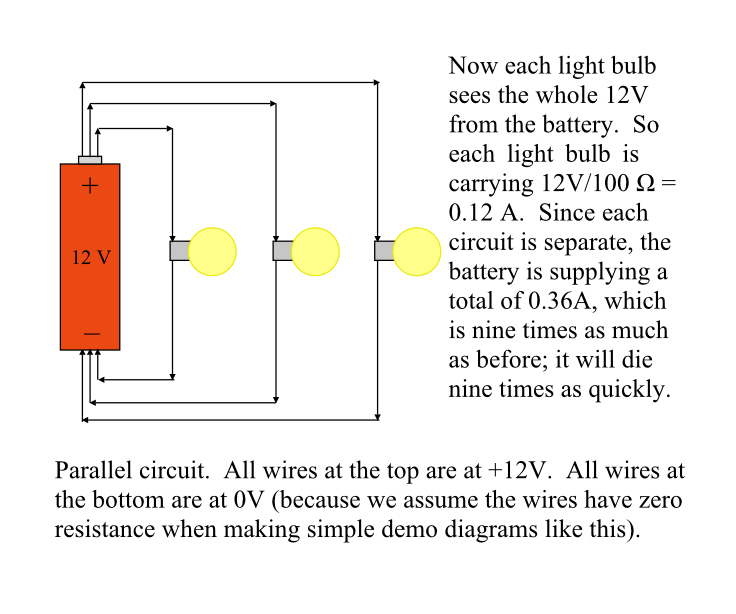
When wiring up a house, if there are, say, multiple lights controlled by one circuit, your electrician wired them in parallel, not in series. (Or he has made a rookie mistake.)

OK, one more thing, before we alas, must call it quits…prematurely.

Imagine a 1A current flowing. That’s one colomb/second (1 C/s). Imagine it’s flowing because of one volt of potential. A volt is 1 J/C.

What happens when you multiply current by potential?

C/s • J/C.

The coulombs cancel, and you’re left with J/s. Which is power, in watts. The same watts we had when we were playing with weights and forces.

(Incidentally, in the US, we tend to think of electrical things in watts–light bulbs especially. But with mechanical things, even an electric circular saw, we think of their power in horsepower. It’d be really odd for someone to brag about how many watts his car engine puts out, though he could. On the other hand, it’s perfectly normal in Europe though even they have a residual use of horsepower, judging at least from car marketing materials (though maybe that’s for the benefit of us Yanks). But just so you have a feel for the difference, one horsepower is 746 watts.)

But this shouldn’t be any surprise. Remember that a volt is what you needed to get a coulomb to do a joule’s worth of work. A current of 1 ampere means that a coulomb of electricity is having this done to it every second, in other words a joule of work is being done every second…which is a watt.

So P (for power) = I (for current…again, don’t ask me why) x E (for voltage).

We can now write many different equivalencies for the watt:

1W = 1J/s = 1V•A = 1 kg•m²/s² = 1 V•C/s…

So we’ve figured out that electricity has potential, it has current, it has resistance and it has power, many of these analogous to gravity, many not really all that analogous at all.

Going back to those two diagrams above, the first has 0.04A flowing through a 12 V potential drop, that’s 0.48 W. The second has 0.36A flowing through a 12 V potential drop, for 4.32W. The latter circuit delivers nine times as much power as the former. Batteries are rated in A•h, not watt-hours, so what matters is how much current it delivers. Because it’s delivering nine times as much current (as well as nine times the power), that battery will die nine times faster.

Now going back to house breaker panels, we know the voltage (on average) is 120V. The breaker says it’s a 20A breaker. Multiply the two together, and the breaker carries 2,400 watts. Why not just label the breaker that way?

Because a breaker is designed to protect the circuit which has a limit on how much current it can carry. The circuit’s capacity is unaffected by the voltage of delivery but it had better not draw more than 20A. In fact the same breaker could conceivably be used in Europe, where the supply voltage is 220V, and therefore be able to pass 220V x 20A = 4,400 watts. (I don’t know if it’s physically compatible with the way their systems are laid out, though, so don’t go selling unused breakers to people in Europe to raise money when the Great Fiscal Apocalypse finally hits.)

There is much, much more to this story, we’re still in the early 1800s. I am sure Wolf will tell you I am quitting before the interesting part. And I am!

But I don’t want this to get overlong, and I still have to draw the diagrams, and it’s already 9PM in Wolf’s time zone.

I’m going to cover a totally different topic next week, then bounce back to this story the week after.

There is a mystery here, you might already see it, but it’s still a mystery in 1895, so let’s save it until we get there.

And Joe Biden didn’t win.

To Be Continued…

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·05·15 Joe Biden Didn’t Win Daily Thread

Another week, another deluge of BS from the White House and from the Controlled Opposition. Not much has really happened, so with that noted, on we go.

On the plus side it looks like the Covid mask is slipping. A lot of places here are now saying no mask if you’ve been “vaccinated.” (And that’s based on the CDC, the governor has not dropped the mask mandate.) The COVIDschina goes on.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices

Gold $1831.70
Silver $27.54
Platinum $1257.00
Palladium $2980.00
Rhodium $27,400.00

This week, 3 PM MT on Friday, markets closed for the weekend

Gold $1844.90
Silver $27.53
Platinum $1232.00
Palladium $2949.00
Rhodium $27,600.00

Gold has broken out, but seems content to stay at this new higher level. Silver has not gone much of anywhere, down one cent. Platinum down (and it had to climb to close at this level today!). Palladium didn’t stay above 3000 for long, but perhaps it will punch through decisively soon, it too was climbing today.

Energy and Potential
(Part III of a Long Series)

Introduction

It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.

Revisiting Gravity with Vectors.

We now know something about vectors, and in light of that, we can go back a ways now to gravitation and take a look at it again.

The law of gravitation we discussed looked like this:

F = Gm₁m₂/r²

But force is actually a vector because it has a direction. This formula is full of nothing but scalars, so it only tells you the magnitude or size of the force vector, not its direction.

If you have a magnitude without a vector, then if you use it to scalar-multiply ia vector of length exactly one, you now have a vector of the right magnitude, because scalar multiplication changes the magnitude of the vector. And if that one-length vector pointed in the right direction, the new vector does too, because multiplying a vector by a scalar does not change its direction.

A vector of length 1 is called a “unit vector” and is a very useful part of the toolkit.

Sometimes it’s necessary to take a vector that isn’t a unit vector and determine the unit vector that matches it.

As you might have guessed, the way to do that is to take your vector, call it V, determine its magnitude, and divide it by the magnitude of V, which is to say, to multiply it by 1-divided-by-the-magnitude. (If multiplication is defined, so is division.)

There’s a symbol for the magnitude of V, and that’s to surround the vector by pairs of vertical lines, like this:

∥V∥

If you’re looking at a diagram, you can measure the vector off the diagram, but if you’re looking at something like [5,-12] how do you know its magnitude?

The answer is you square every element, add them together, and take the square root.

In this case, you’ll want the square root of 5•5 + -12•-12. Doing the arithmetic, you’ll want the square root of 25+144=169, which happens to be 13. So ∥[5,-12]∥ = 13.

This also works in three dimensions, consider [3,4,12], whose magnitude is the square root of 3•3+4•4+12•12 = square root of 9 + 16 + 144 = square root of 169 = 13 (again).

If you noticed something eerily familiar about this, that’s because this is also the Pythagorean theorem, the one about the square of the lengths of the legs of a right triangle equaling the square of the length of the hypotenuse. This makes sense, because the individual pieces of a vector are at right angles to each other.

Figure 3-1 determining the magnitude of a vector, and its relationship to the Pythagorean Theorem

Now that you have your magnitude, you can divide your original vector by it to get a unit vector. So [5,-12], turned into a unit vector is [5/13, -12/13]. That vector has a length/magnitude of 1. A more common example is [3,4] which has a magnitude of 5. The unit vector is a nice tidy [0.6, 0.8].

So a unit vector corresponding to some vector V is V/∥V∥. Usually physicists and mathematicians will write the letter with a “hat” on it (for example, Â) to denote it’s a unit vector, but unfortunately not every letter has a version with a hat on it available in unicode (at least not on this machine), so I’m a bit constrained here. You might have to get used to the V/∥V∥ long form.

So let’s get back to gravity. We have the formula for the magnitude, how do we turn that into a vector? We multiply by some unit vector. Which unit vector? The one pointing in the right direction of course. (OK, smartass, what’s that?) We know that the direction of the force on an object due to gravity is towards the attracting object.

Let’s call the force by body 1 on body 2 F₁₂. (Note the order of the subscripts, the first is the attracting body, the second is the attracted body.) The direction of that force is from body 2 back to body 1. So you can draw a vector, r₂₁ from body 2 to body 1, unit-ize it, and you have your unit vector.

Actually, typically the vector is drawn from body 1 to body 2, the opposite direction, so we will write the formula in terms of r₁₂. That vector is simply the opposite of the first one, it’s equal to -1 times the first vector.

r₁₂ = –r₂₁. Which of course means that r₂₁ = –r₁₂.

Figure 3-2 The Universal Law of Gravitation, as vectors.

So we can write our vector version of Newton’s Law of Gravitation at last. (Edit: found an r-hat character!)

F₁₂ = -(Gm₁m₂/r²) ȓ₁₂

Notice the minus sign, which points the force vector back at the first object.

Energy

OK, so now we’re ready to proceed on to the subject of energy.

This is actually a concept that turns up again and again (and again, and Joe Biden didn’t win), in many different forms, the most basic of which is “work.”

Work, to a physicist, is what is done by a force acting on a body through a certain distance.

If I push on some object (on a frictionless surface, or out in space) and it moves some certain while I’m doing it, the work I’ve done is equal to the force I applied, times the distance.

W = Fd

Note that the distance traveled might not be due entirely to the push I gave the object. If it was already moving in that direction before I pushed on it, I’m still doing work on it by applying a force to it, even if most of the distance it traveled while I was pushing was due to the speed it already had.

(The key words are “in that direction”. If it’s moving at a 90 degree angle to the push I gave it, it has zero effect on the work done. I will have lots more to say about this, further on.)

So as a scalar, that’s just Work = Force x distance. But force is measured in Newtons or kg•m/s². Working with metric units, that’s N•m, pronounced “Newton meters.” You can break it down further, since a Newton is a “kilogram meter per second-squared”, multiply that by “meter” again for the distance, and show that a “Newton meter” is also a “kilogram meter squared per second squared:

Work is measured in: kg•m²/s²

This is another named unit, the Joule, after James Prescott Joule, who in the 1840s performed a number of experiments showing that the sorts of energy we’re talking about today could be converted to heat (more on that later). The Joule in fact is the standard metric unit of energy.

So here’s a simple example. On Earth, a one kilogram object falling one meter, has 9.8 Joules of work done to it by the force of gravity. Let me back that up with the math. The force of gravity on that one kilogram object must equal its mass times the acceleration (F=ma); the acceleration due to gravity on Earth is g = 9.8 m/s². (Little g is often used as a symbol for Earth gravity. Don’t confuse it with Big G, the gravitational constant or fudge factor from the first post in this series.) The mass is 1kg, so multiplying 1kg•9.8m/s², the force is 9.8 Newtons, pointing straight down. (In fact, “down” is defined as the direction gravity pulls, so no coincidence.)

This is acting on the object over a distance of one meter, straight down, so it’s 9.8N x 1m = 9.8 N•m = 9.8 J.

It’s not just gravity. As alluded to earlier, you can push on an object, a rocket can push on an object. So long as it moves in that direction while you’re doing it, you’re doing work.

If you start at a standstill, and continuously apply the same force to an object, its acceleration stays the same. F=ma, or more to the point, a=F/m. The distance covered, d is equal to ½at² (where t is the time you spent pushing it).

d=½at²

So if a is one meter per second per second, after you’ve spent one second applying the force, you’ve moved that object half a meter (½•1 m/s² • 1•1s² = 1m) = 1. After two seconds, you’ve moved the object two meters (½•1 m/s² • 2•2s² = 4/2 =2m). After three seconds, you’ve moved four and a half meters (½•1 m/s² • 3•3s² = 9/2 =4.5m). And so on. Basically, in this case square the number of seconds and divide by two.

If your object has a mass of one kilogram, the work done in the first second is 1m/s² x 1kg x 0.5m = ½ of a Joule. In the second second, though, you travel one and a half meters (bringing the total up to 2 meters). So now the work done in that 2nd second is 1m/s² x 1kg x 1.5m = 1½ Joules. So it seems like the longer you push the more work you do every second!

That moving object is now moving at 2 meters every second. And you’ve dumped a total of two Joules into it, working on it.

After three seconds, the total is 3 meters per second, and the work is 4½ Joules.

The work you’ve done on the object is manifesting itself as motion. Work is a form of energy, so is motion. Both are measured in Joules.

So let’s look at this again, cumulative totals:

t = 1 s d = 0.5 m speed = 1 m/s work done and KE = 0.5 J.
t = 2 s d = 2.0 m speed = 2 m/s work done and KE = 2.0 J.
t = 3 s d = 4.5 m speed = 3 m/s work done and KE = 4.5 J.

Notice the KE and speed match up like this: KE = ½v². But actually, that doesn’t account for the mass. If you were to push a 2 kilogram mass with twice the force, the acceleration would be the same, but the work would double, and the kinetic energy the work does would also double. So the correct formula is:

KE = ½mv²

OK, a quick sanity check. I’m saying that kinetic energy and work are both forms of energy. One way to check that, is to look at the units. Actually, more precisely, the dimensions (distance, mass, time, rather than meters, kilograms and seconds). If the dimensions are different, they can’t be the same thing.

So: Work is force times distance. Force is mass times distance divided by time squared. So, combining, work is mass x distance / ( time x time ) x distance, or more compactly, md²/t².

And kinetic energy is mass times speed squared, speed is distance over time, so combining, KE is mass x distance x distance / ( time x time ). Gathering things together, it’s md²/t².

They match, so they could be equivalent.

And indeed they are, though I won’t be proving that here!

One thing I haven’t mentioned is whether energy is a scalar or a vector. It happens to be a scalar.

OK, let’s go back to that other 1kg object, the one that fell one meter and thudded onto the ground.

Let’s lift it back up one meter, back to where it fell from. Let’s do it smoothly.

While the object is being lifted, its speed does not change. Which is to say, it’s not accelerating. So the net force is zero.

But we know that gravity is always pulling down on that kilogram with a force of 9.8 Newtons. So for the net force to be zero, we must be applying a 9.8 Newton force upward.

Since we’re lifting the object one meter, the work we’re doing on it is

W = 1m • 9.8N = 9.8 Joules.

None of this is kinetic energy, though. What happened to the hard work? I’ll tell you presently.

In this specialized case of working against gravity, you can use a fairly simple formula for the work done:

W = mgd

Where g is the acceleration due to earth’s gravity, m is the mass, and d is the distance. But that’s not quite right.

To see why, let’s go to another scenario.

You’re pulling an object, say a hundred kilograms, up a very slick (frictionless) ramp (you’re doing this because lifting the dang thing straight up is hard!).

And you’re doing it smoothly, like with the lift of the one kilogram object, neither accelerating nor slowing down on the ramp.

If the ramp is 2 meters long, can’t you go back to your formula and figure out the work?

W = mgd
W = 100kg • 9.8 m/s² • 2 m = 1960 J.

But that seems wrong. What if the ramp is almost flat? Versus a ramp that is almost vertical? If those are both 2 meters long, the vertical ramp is obviously more work!

If the 2 meter ramp is at a 30 degree slope, it turns out that the top end of it is 1 meter higher than the bottom end. (Thirty degrees is a “magic angle” in trigonometry. And if that means nothing to you just ignore it, as I’m trying to avoid trigonometry in these articles.)

Intuitively, what matters is the vertical distance traveled. Not the horizontal distance. And if you think about what work is, it’s applying a force. No force is being applied in the horizontal direction, because the object isn’t speeding up or slowing down and there’s no external force in that direction either, gravity points Straight Down.

So you need a way to take your motion as a vector, and use only the component of the motion vector in the same direction as the force to compute the work.

Because your motion and the force you’re countering are both vectors.

So what is the vertical height of the ramp? I just told you, it’s 1 meter. So 1 meter times the force of gravity gives you the right answer.

Figure 3-3 Dragging a block up a ramp, analyzed by breaking down the slope of the ramp in terms of the force.

But there’s another way to analyze this! In fact, it’s probably a bit better. You could instead take the component of the force of gravity, in the direction of the slope of the ramp! After all that’s what you’re actually countering by pulling on the rope.

Figure 3-4 Dragging a block up a slope, analyzed with the components of force in terms of the ramp

Note in red, the vertical vector is now broken down into an up-the-ramp component and a perpendicular-to-the-ramp component. Because 30 degrees is a magic angle, I know the force up the ramp is half the total, or 490N.

Now it is entirely appropriate to use the 2 meter length of the ramp, because it’s in the same direction as the force you are applying. 2m x 490N = 980J of work.

This is why ramps are useful, by the way. You can counter the force of gravity by applying very little force. In this case, half as much. The price you pay is you have to apply that force over greater distance, in this case twice as much. You could reduce the force as much as you want, if you have room and material for a longer and longer ramp.

Dot Products

Gee, it’d sure be nice if you could do this computationally. Well, you can. You can do trigonometry to determine that 1/2 factor for 30 degrees, or whatever it is for any other angle.

Gee, it’d sure be nice if you could do this computationally, without trigonometry. (After all, you don’t want to have to pester a geek and OMG! make him feel useful doing the trig for you.) Well, you can, if you have the vectors!

We do have them. The force we have to apply is [0, 980]N. The amount of distance is 2 meters, but we need the rise and run from the first diagram to be in vector form: [1.732, 1.0]m

[Trivia note: 1.732 is the square root of three (rounded to three decimal digits). Like I said, 30 degrees is a magic angle, the legs with a hypotenuse of 2 are 1 and sqrt(3). It’s easy to remember the square root of three because its digits spell out Washington’s birth year, 1732. If you’re a coin geek you can remember that because the Washington Quarter we use today began to be issued in 1932, his bicentennial. If you’re just a regular geek, you probably don’t know Washington’s birth year, but you probably do have 1.732 memorized and can use it to remember that Washington was born in 1732.]

OK, we have our two vectors, F=[0, 980]N and d=[1.732, 1.0]m

Here’s what you do. Multiply the first elements together, then the second elements, then the third elements (if you’re working in 3D), and if you’re playing 64 D chess, do the same for elements 4 through 64. Just keep going until you’re out of vector.

In this case, I end up with first elements: zero, and second elements: 980N•m. Done.

Add those numbers (all two of them here, all sixty four of them if you’re Donald Trump) and get, 980N•m.

You didn’t have to do any trigonometry! You didn’t have to break the vectors down into components, not in x-y or even along some cockeyed slant!

What we just did was to take the dot product of the two vectors, in other words we computed F∙d. That’s the real, vector form of the formula for work.

W = F∙d

Now I sometimes use a dot to show multiplication, particularly when I’m showing multiplying two actual numbers, or units. I’m having to use a big fat dot here, to distinguish the vector dot product from the just ordinary multiplier dot. (Note: It shows on my computer doing edits in a file, it isn’t showing up in the post editor, and may not show up as a big dot when it posts. We’ll find out, sometime before you read this!)

There are two things you may have noticed.

One, I’m talking about the dot product, not just the product; as if there were some other kind of product. With vectors, there is. Don’t worry…you’ll find out some future week! (Evil laugh!)

And another thing…the result of a dot product, is a scalar.

Work is a scalar. Kinetic energy is therefore also a scalar. Energy has no direction.

OK, let’s have a little more fun with the dot product. Take some vector, like v = [3, 4, 12]. Let’s take the dot product of it with itself, v∙v

That’s 3•3 + 4•4 + 12•12.

Does this seem familiar? Like maybe we did the exact same thing earlier in this marathon of post, while figuring out the magnitude of that exact same vector?

Except that when getting the magnitude we went on to take the square root. With the dot product we don’t do the square root. So the dot product of a vector by itself is the square of the magnitude. So, here’s a rule:

For any vector v: v∙v = ∥v∥²

Another rule. If two vectors are perpendicular, their dot product is zero!

I’m going to make up a four dimensional vector off the top of my head (I promise, I just made it up off the top of my head):

[12, -7, 9, -15]

I can make up another four dimensional vector and know that it’s perpendicular to this one, without having to draw a diagram. Which is good because my supply of four dimensional paper is a bit low right now. (The COVIDschina has caused all kinds of supply chain havoc.)

OK, let’s just make the first element of the second vector 9, and the second one 9 as well. You could literally pick any numbers for all but the last one. Make the third element -20. Let’s hold off a bit on the fourth one, and call it x.

[9, 9, -20, x]

I can take the dot product of this, it’s 108 + -63 + -180 + -15x, combining I get -135 + -15x, which has to equal zero if the vectors are to be perpendicular. It turns out if the last element is -9, the last bit of the cross product is +135 and the total is zero. (I was lucky, I didn’t end up having to multiply by an ugly fraction at the end.)

So even though I can’t draw a diagram of these two vectors, I know, like I know that 2+2=4, that [12, -7, 9, -15] and [9, 9, -20, -9] are perpendicular, because their dot product is zero.

If two vectors are parallel, but of different sizes, the dot product will be the product of their magnitudes. For example, [3, 4] and [6, 8] are parallel, because the second one is just 2 times the first one. Take the dot product, 3•6 + 4•8 = 18 + 32 = 50. If you do Pythagoras on those two vectors, their magnitudes are 5 and 10, which multiply together to make 50.

And that’s as far as I can take you without trig. There is a rule that tells you how big the cross product will be in terms of the two vector magnitudes and the angle between them…but, trig. (Fortunately the geeks here who know trig probably already know the rule.)

Potential Energy

OK, let’s return to the 100 kilogram block we pulled up the ramp, lifting it a meter, doing 980J of work.

In this case once we stop lifting the object isn’t moving. So our work didn’t become kinetic energy. What happened to it? It became potential energy. It’s basically stored in the object, as if it were a battery. To get it back, we drop the object, pretending to do so on some deserving Deep State puke’s head. (Maybe we can lay their picture flat on the ground.)

On earth, at least, we already have a formula for potential energy. It’s the work we put into it, the mass times the acceleration due to gravity times the distance. Only instead of d let’s use h for height, because that’s in the same direction as the force.

PE = mgh

where h is the height above the ground. Its distance times force, and force is in turn mass times acceleration due to gravity, g (9.8 m/s²).

So the object has potential energy. If you want the kinetic energy back, drop it, but then the object is back on the ground and the potential energy is gone.

(Note that we’ve been behaving as if the ground is the place where potential energy is zero. In fact, your choice of where zero is, is completely arbitrary. Imagine dropping the object down a well. If the potential energy is zero at ground level, it’s actually a negative number at the bottom of the well. As it turns out physicists like to put the zero point at infinity, and you’ll see why in a moment.)

It’s almost as if you can swap kinetic and potential energy freely.

Indeed, in many circumstances you can. If you don’t have to deal with friction, and other objects getting in the way, you can do it. One place where this is true is in space, there you only have to deal with gravity. In our discussion so far we’ve ignored everything else, so it won’t be quite accurate–you won’t quite get all the energy back when you drop the object, because of air resistance, no ramp is frictionless, and so on, but in space, there actually is nothing else.

An object’s kinetic energy, plus its potential energy, put together are called the mechanical energy and in space, for some given object in orbit, this is a constant.

So let’s look at kinetic versus potential energy in space.

Kinetic energy, we know how to deal with. But there’s a bit of a wrinkle with potential energy. On earth we deal with lifting an object a short distance, and the force of gravity is effectively constant over that distance. But when in space, you are not dealing with a constant force. Gravity measurably weakens the further you get away from Earth. So PE=mgh won’t work as a formula for potential energy. Instead, when dealing with potential energy with respect to the Earth, it’s –mm_eG/r, with m_e being the mass of the Earth, G being the gravitational constant/”fudge factor” and r being the distance from the center of the earth. And as always, our object’s mass is m. If r is set to infinity, the potential energy is zero. As you get closer to the Earth, the number becomes more and more negative, reflecting less and less potential energy. This formula is only valid above the surface of the earth. Below the surface gravity again decreases. If the earth were a point mass, the formula would be perfect (and the Earth would be a black hole).

m_eG is also known as μ_e, the gravitational parameter of the earth, and that is 3.98×10¹⁴m³/s². So our potential energy formula is now:

PE = –mμ_e/r = – 3.98×10¹⁴m/r

The earth’s radius is 6,378 km (through the equator, not elsewhere, but let’s use it), that’s 6,378,000 meters. So at the surface of the earth, the potential energy of a one kilogram object will be -62,402,000 Joules.

So it stands to reason that if you can give a one kilogram object 62.4 million Joules of kinetic energy, it will keep going until it’s an infinite distance away, having traded all of its kinetic energy for potential energy and bringing the potential energy up from looking like a millionth of the national debt all the way to zero.

Whatever that speed is, it’s the escape velocity of Earth. Impart it to an object on the surface, and it ain’t ever coming back!

Remember:

KE = ½mv²

But this time we know the kinetic energy and we want the velocity. So doing a bit of rearranging:

v² = 2 KE/m

So simply multiply the 62.4 million Joules by two and divide by our mass of one kilogram, then take the square root. The square root of 124.8 million is 11,171.4 meters/second. That works out to 6.94 miles per second. And that’s our escape velocity, at least as seen from the surface of the Earth.

You can do this whole thing again with, say, a 57 kilogram object. The potential energy on the surface is 57 times as much (a bigger negative number), the KE is 57 times as much, but you divide out the mass. So the escape velocity is the same.

Now, let’s consider an object in a perfectly circular orbit. It will have a certain potential energy. It will also be moving at a constant speed. The sum of the potential energy and the kinetic energy, therefore will remain a constant.

But this is true in an elliptical orbit, too!

With an elliptical orbit, one end of the ellipse is as far away as the orbiting object ever gets away from Earth (the apogee, or more generically for any body, the apoapsis), the maximum potential. The other end is as close to the Earth as the object ever gets, the perigee or periapsis. It has a lower potential, which means the kinetic energy must be higher to make up for it. And indeed, if you’re in an elliptical orbit (around anything) you will speed up the closer you get to the object you are orbiting.

Figure 3-5 Conservation of mechanical energy in an elliptical orbit

And in space, with no friction and no objects getting in the way, provided nothing comes along and disturbs that orbit, the object will go on circling, swapping potential for kinetic energy and back again, with perfect efficiency, forever. The mechanical energy, PE + KE, equals some constant. In fact, it’s zero if the object is moving at escape velocity, since PE + KE cancel each other out perfectly at that speed.

Something that doesn’t occur to most people. If the mechanical energy is zero, it will always be zero, and the object is always moving at escape velocity, no matter how far away it gets from Earth; it’s just that escape velocity is lower the further away you get. It also doesn’t matter which direction it’s going. It could even be going almost directly towards Earth. It’s still never coming back, as long as it doesn’t come so close to Earth that it collides with Earth. The one other thing you can say is that the path it traces will be a parabola.

When someone asks “what’s the Earth’s escape velocity?” they almost certainly mean “at the Earth’s surface.” So give them that 11 thousand something. But it’s different if you’re already ten thousand miles up!

If the mechanical energy is greater than zero, it’s not only going fast enough to escape Earth, it’s got surplus velocity to boot. (And it will travel in a hyperbola.) If the mechanical energy is less than zero, it will eventually reach a maximum distance and start coming back. It’s in a closed orbit, which will be an ellipse of some kind, a circle being the limiting case (all circles are also ellipses). The lower the total energy, the smaller the ellipse.

So under a certain idealized set of circumstances, mechanical energy is conserved.

What about other circumstances? Mechanical tends to bleed off, and decrease, especially that part of it that is in the form of kinetic energy. Think of a pendulum, that’s another “ideal” case of swapping kinetic for potential energy; the pendulum swings fastest at its low point, and is motionless at the top of its swing for a split second. It’s clearly trading potential and kinetic energy back and forth, over and over. But a pendulum is moving through the air, and air resistance will take a little bit of speed off that pendulum, so it won’t rise quite as far on the upswing. Over and over again, the pendulum swings less and less and eventually stops. It would go on longer in a vacuum, but the pivot point introduces some friction, too.

Friction is the nemesis of mechanical energy. The more friction, the more energy bleeds out of the system (unless it has no kinetic energy to begin with, think of a rock on a mountain top).

What happens to things when friction is going on? They heat up. So mechanical energy is being turned to heat.

Heat and Chemical Energy

As it turns out, heat is yet another form of energy. Our friend James Joule helped figure that out.

Heat, it turns out, is measured a bunch of different ways. The amount of heat necessary to raise the temperature of water one degree Celsius/Kelvin is defined as a calorie; a thousand of those is a kilocalorie (kcal), or sometimes Calorie with a capital C. That “big C” calorie is what you count when you’re on a diet, a food Calorie, and since heat is energy, it turns out that a Calorie of heat is 4,184 Joules. Chemists tend to use calories and kcal because they heat water a lot, then convert at the very end to Joules. They have 4,184 memorized. (I had to look it up.) It’s easy to work with calories when dealing with water. How many grams of water times how many degrees C you heated it up.

Not only is heat another form of energy, it’s the garbage can of energy. You can convert kinetic energy into heat, like by the energy of impact heating up whatever got hit, but you cannot convert all heat back into kinetic or potential, or any other kind of energy, only some of it. So energy tends to accumulate as heat over time, and this process is not completely reversible, so eventually all energy in the universe will be unharnessable heat. This is a consequence of thermodynamics. We’ll be out of usable energy. That is an energy crisis! Fortunately this is trillions of trillions of years off in the future, so you’d better do your taxes, but still, thermodynamics is the real “dismal science” because it tells us the universe is running down. You can’t win, you can’t break even, and you can’t quit the game.

This is also why any generating plant that relies on heat is not perfectly efficient. You burn the coal to heat the water into steam, you use the steam to turn a generator…but you can’t harness all the energy you put into the water and turn it into electricity, because that energy is all heat. Some is lost to practical use…forever. In fact a coal plant engineer would do cartwheels down the hall if he could get the plant to 35% efficiency. Two thirds of every pound of coal burned is wasted.

There is also energy in chemicals. That should be obvious by now since food contains kilocalories. Obviously, you can get that energy out by burning things. But it comes into play in another way. If you are James Comey, and you finally got your comeuppance and you’re having to make little ones out of big ones while waiting for your date with the executioner, you’re taking a big honkin’ sledge hammer, giving it a lot of kinetic energy, and smacking it into a rock, which breaks.

It take energy to break a rock. And that’s because the rock is full of chemical bonds that have to be broken, that’s a facet of chemical energy. The rock lost energy being formed, you’re resupplying it to break it back apart.

And when you eat bacon, you end up “burning” a lot of that fat for energy, and that is a chemical process.

A huge part of chemistry is tracking the energy through chemical reactions, supplying some where needed, using it where it’s given off. And reactions that give off energy and leave the reactants with less total energy tend to be favored; chemicals like having very little energy bottled up inside them. (There are plenty of added complications here; I won’t trouble you with them, but they are the reason paper doesn’t just burn spontaneously at room temperature.)

Conservation of Energy

OK, let’s take these other forms of energy into account (and others I haven’t even mentioned). What then?

You find that energy is conserved. In a closed system it is never created from nothing nor is it destroyed, though it can be converted from one form to another. So we have our third conservation law. We now have mass, momentum and energy conserved.

And that is another part of the state of physics in 1895.

Potential

I want to drop one more concept on you. The concept of potential. Not potential energy, just potential.

Consider a rock at the top of a cliff. It has a decent amount of potential energy, right? Another rock right next to it twice as massive has twice the potential energy. Or you could find a rock of the same size on a cliff twice as high. The point being that the potential energy depends on the vertical distance and the mass of the object.

Sometimes it’s very convenient to divide by the mass. When you do that with potential energy, you get potential energy per unit mass, also known as specific potential energy, or just plain potential. The two rocks at the top of the same cliff have the same specific potential energy, the same potential. But the rock at the top of the other cliff has twice the specific potential energy, because the cliff is twice as high.

You can turn potential into “how fast will that rock be going when it hits the ground, if it falls off the cliff” because that does not depend on the mass of the rock. Gravity accelerates all things equally, because the more massive the object, the more the force increases.

And with orbital mechanics, the satellite is usually such a tiny fraction of the primary’s mass, we divide the mass out of everything, turn the forces into accelerations, the potential energy into potential, and just square the velocity and divide by 2, because the mass of the satellite never changes, and if it does, so do the forces on it, it’s kinetic energy, and potential energy all in proportion. You’ve seen a hint of this in g being the acceleration due to gravity, not the force due to gravity. It’s more convenient to work with since the mass really doesn’t affect velocity, acceleration, or position.

I didn’t bring this up gratuitously. Potential will turn ot to be an important concept down the road, particularly when we look at electricity.

OK, now on to our 1895 mystery:

What makes the stars shine? (Introducing Power)

This is a big one. Almost everything we can see in the universe is a star. The planets here and out there are an insignificant fraction of the visible matter in the universe.

So if we can’t figure out the stars, in one respect we don’t know Jacques Schitt (or Adam Schiff) about the universe.

OK, so let me try to summarize what they had figured out in 1895. The stars shine, actually, because they’re hot. In the same way that embers in a fireplace glow. But stars are much hotter, the light they put out is whiter (true even for “red dwarfs”), and they put out a lot more of it. Physicists had done work on this “black body” radiation and could describe it really well, though they couldn’t figure out just yet why stars (and embers) didn’t radiate more at even higher frequences (bluer light and even ultraviolet)

But something that is glowing because it is hot, is actually shedding heat that way. Eventually it will cool off, stop glowing and assume ambient temperature.

So really, the question is what makes the stars continue to shine.

And that is a very good question. In order for a star to not just go dark, it must be accessing the same amount of energy every second that it puts out in that second. If it’s getting less energy, it will start to cool off, if it’s getting more, it will heat up. Most stars are fairly stable, so there must be a balance: energy radiated must equal “fresh” energy used to heat up the star.

We are talking about a rate of energy consumption, naturally expressed in Joules per second (J/s). That, folks, is power, and is measured in Watts. Yes, the Watts you know from light bulbs. Chances are good you didn’t know Watts are a metric unit!

The sun, to take a well known example, is pumping out 3.828 x 10²⁶ watts. It’s doing so in all directions, so our little dinky Earth 150 million kilometers away gets only a minuscule fraction of it. Some of it hits other planets, the rest just blasts off into space, a ridiculously tiny fraction of it will hit other stars and their planets and maybe be seen by aliens.

Where does the sun get the 3.828 x 10²⁶ Joules it needs every second to sustain this?

Let’s go over the possibilities that people had come up with. Chemical energy? What if the sun were a gigantic sphere of coal and it were being burned?

Well, we know how big the sun is, and we know its mass. We know how much energy coal releases when it burns. (We know that very well, since our economy largely depends on it.) If the whole thing were coal and were burning to pump out that kind of wattage, it would last 1500 years.

Which means the sun wouldn’t last the span of time since the fall of the Western Roman empire. Well, we have daylight now, and had it back then, so…scratch chemical energy. There are things that release more energy than coal, but not that much more; we can’t get from the pyramids to today.

But we already know kinetic energy can turn into heat, so what if a lot of meteors are hitting the sun, continuously? As it happens, if 1.2 x 10¹⁷ kg of meteorites were to hit the sun at its escape velocity every second, that would be enough to do it. That’s 120 trillion tonnes of stuff, every second!

But there’s no evidence that there’s that much junk hitting the Sun. Some of it would surely hit Earth and meteor strikes would be a lot more common than they are. Besides, this much mass falling on the sun would add one percent to its mass every 300,000 years. Increasing the mass of the sun increases its gravity, and we, monitoring planets orbiting the sun, would definitely know if this were happening, because the planets would gradually get closer to the sun and speed up in response to the mass change. Each year would be two seconds shorter than the year before, and there’s no way we’d miss that.

Finally, the best suggestion…though not good enough…came from Herman L. von Helmholtz in 1853. He was one of the people who first formulated the law of conservation of energy, so you can be sure he took that into account when making his suggestion. Why use meteorites, when the sun itself could be contracting and not gaining mass? If the material at the surface of the sun is in fact still falling towards the center, it’s converting potential energy to kinetic energy which can heat the sun up.

Helmholtz calculated that if the sun were shrinking 0.014 centimeters every minute, that would actually release the energy needed.

That works out to a mere 560 miles (out of a total diameter of 864,000 miles) in the roughly 6000 years of recorded human history, and again, this does not involve altering the mass of the sun at all. That total is a lot less since the invention of the telescope; small enough we could not have measured it as of 1895. (We’ve had more time since then, and our tech is better. Maybe we could do it today.)

So it looks promising. But running the clock backwards, the sun would have been big enough to swallow up the earth in its orbit at some time in the past, and that was calculated to be 18 million years ago. That’s a maximum age for the sun and especially the Earth, if that’s how the sun gets its energy. If it were any older than that, Earth wouldn’t exist today.

And that’s not nearly long enough. Geologists had plenty of compelling arguments that the earth must be hundreds of millions of years old, if not billions. And evolution needed time to act too. The theory had been put forward in 1859, and biologists were becoming convinced. Those were two independent arguments against a less-than-eighteen-million-year-old Earth.

So we have astronomers saying the sun can’t be that old, and geologists and biologists saying it must be that old. Who was wrong? Well, there was tangible evidence for the old earth, against physicists and astronomers not knowing how it could work; they were basically arguing from ignorance, and they knew it.

So they were willing to believe it was old, but that meant they had no idea what was powering the sun.

And that applied to all the other stars in the universe, too.

What’s powering the sun and every other star in the universe?

No one had any real idea, as of 1895. And remember, most of the visible universe is stars, and we didn’t understand them, so we really didn’t understand much, on a weight basis.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

To conclude: My standard Public Service Announcement. We don’t want to forget this!!!

Remember Hong Kong!!!

If anyone ends up in the cell right next to him, tell him I said “hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·05·08 Joe Biden Didn’t Win Daily Thread

His Fraudulency

Joe Biteme, properly styled His Fraudulency, continues to infest the White House, we haven’t heard much from the person who should have been declared the victor, and hopium is still being dispensed even as our military appears to have joined the political establishment in knuckling under to the fraud.

One can hope that all is not as it seems.

I’d love to feast on that crow.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices.

Kitco Ask. Last week:

Gold $1768.60
Silver $25.97
Platinum $1205.00
Palladium $2996.00
Rhodium $29,000.00

This week, markets closed as of 3PM MT.

Gold $1831.70
Silver $27.54
Platinum $1257.00
Palladium $2980.00
Rhodium $27,400.00

That is a big breakout for gold on the upside. It went up fifty dollars just since Wednesday. Platinum hasn’t done too badly either! It went up over $30 on Wednesday.

(Be advised that if you want to go buy some gold, you will have to pay at least $200 over these spot prices. They represent “paper” gold, not “physical” gold, a lump you can hold in your hand. Incidentally, if you do have a lump of some size, doesn’t it give you a nice warm feeling to heft it?)

Update: More info on Valcambi Combo Bars

Somebody asked me about the Valcambi combo bars for gold, silver and other precious metals. These are the ones that can readily be broken up into smaller pieces. I was at the Denver Coin Expo yesterday/Friday, and asked someone who had Valcambi bullion at his table if the bars were worth less broken apart, and he said yes, they are worth less.

Still, it might be worth holding a couple of them (and not breaking them apart) in case there’s a fiat money apocalypse. If that happens, you’ll have bigger problems than worrying about how much fiat you’ll get for a 1 gram bar as opposed to the full, 20 (or more) block chocolate bar, and it might be a good way to subdivide your gold holdings when you absolutely need to. Or, you can use silver for “small” change…but even there, it might make sense someday to be able to break down an ounce of silver.

Velocity and Momentum
(Part II of a Long Series)

Introduction

It’s such a long story I decided to break it down into pieces, and this is the second of those pieces.

A couple of Go Backs

Remembering my previous post on mass, one might wonder, “why bother with this sort of thing? Why should people investigate such things?”

We live in an orderly universe. This is a good thing. It gives us confidence that when we set the groceries on the counter, they won’t jump up and bite us. (Not even Darwin’s live food groceries.) It also means that when we drop a car battery on our feet, we know it!

The point of science, when it is being properly done, is to increase our understanding of this world we are in.

All that work on forces and masses and weight was at its core an exercise in breaking down phenomena we see every day into different effects and studying one of them. We removed friction and gravity from the picture and analyzed what was left. Then we took up gravity. What we didn’t get to was showing that friction is itself a force.

With that kind of understanding, you can predict what will happen in an environment where gravity is different, e.g., on the moon and in orbit. At first you won’t be used to it, but then you do get used to it. There are plenty of stories of astronauts who adapt so well to “microgravity” (i.e., the lack of any sort of sensation of “down”) and free fall that they will come home, put the toothpaste on the toothbrush, and drop the toothpaste tube, because they’re used to just letting it go and having it stay there until they’re ready to put things away. They’re applying Newton’s first law (objects at rest will stay at rest) since it is pretty much unmodified in orbit, no need to worry about gravity pulling things to the floor.

Another Go Back. Last time I rather casually used the concept of acceleration, without really going into it much. I assumed some knowledge that many might not have.

You can think of acceleration as change in speed, the faster the change, the greater the acceleration. And it can be a decrease as well as an increase; to a physicist it’s still an acceleration, albeit one which is in the reverse direction to the motion.

I know, too, I said things like “meters per second per second” a lot. That wasn’t a stammer. That’s truly how you measure acceleration. Think about a sports car, able to go from zero to 60 miles an hour in four seconds. That means, on average, every second of that four seconds, the car’s speed increases by 15 miles per hour. So it accelerates at 15 miles per hour every second, which is to say at 15 miles per hour per second. That can even be written as 15 miles / hour / second (the “per” functioning as a division). Or even, 15 miles • 1/hour • 1/sec.

Yes, when physicists do math, they will multiply and divide by units, not just the numbers. They can be divided and multiplied, and even follow the rules of cancelation. (Chemists often have to convert from one unit to another, like calories to Joules, so they really do this sort of thing a lot.)

Notice there are two time units (hours and seconds) in the denominator. It’s kind of funny that they don’t match. You could convert the hours into seconds, like this: Use the fact that there are 3600 seconds in an hour and do the following: 15 miles • 1/hour • 1/sec • 1 hour/3600 sec.

That last term is simply 1 hour divided by 3600 seconds, which is 1. You can multiply by 1 without changing anything. But now that it’s there, the two hours, one in the numerator and the other in the denominator, cancel

Do that cancellation and you have 15 miles • 1/hour • 1/sec • 1 hour/3600sec, and you can re-arrange to get 15/3600 • miles/sec/sec or 1/240 miles per second per second or 0.004167 miles / sec². You could then move on to convert miles to meters (1609 meters is one mile, roughly), and that works out to be 6.7 m/s², and it turns out that car is accelerating about 2/3 as much as gravity accelerates a falling object.

You may have noticed I seem to prefer metric, and that’s because just about every bit of my technical education was in metric; I’m used to it. When I got exposed to the occasional rocketry done in pounds force and pounds mass, it was like trying to use stone knives and bearskins (and you needed to know when you had to multiply or divide by that 32). Obviously it works (we put men on the moon after all), but it just seems cumbersome to me.

(And a note for the fussy, you’ll notice I’ve sometimes spelled out a unit, e.g., “second” and sometimes abbreviate it “sec” or “s.” That last one, just a plain s, is the “official” metric abbreviation for second. Likewise meters, m, and kilograms, kg. But sometimes I spell things out too, as a reminder.)

But the notion of acceleration (however you measure it) is itself depends on speed…actually, it is dependent on velocity.

Velocity

So my second “go back” actually leads us into today’s topics. Let’s flesh out velocity.

Velocity is both how fast something is moving, and in what direction. So it’s actually a more complex concept than the one we talked about last time, mass. The distinction between mass and weight was probably odd to many, but at least mass can be expressed as a number. Velocity? You need a number (your speed), and a direction. (Or maybe you can get by with a bit less…stay with me.)

Direction is easy on a straight highway. You’re either going forward or backward. Since there’s only two choices, and they are opposite of each other, it’s natural to consider the forward direction positive and the backward direction negative. So driving 60 mph in fourth gear is +60 mi/hr, but switching to reverse (after first stopping, since we don’t want your engine to leap through your hood in an ugly mess), and going fairly fast in reverse might get you -10 mi/hr. The local constabulary, using a radar gun, will measure your speed and may depending on circumstances pull you over to inform you how fast you were going and how much you will have to pay for that.

You can even add and subtract your velocities, just like you do with masses. The usual example here is a railroad car moving along on tracks, also nice and tidy and one-dimensional. If the train is moving at 60 mi/hr and a pitcher is in a cattle car, playing catch with someone, and he throws the ball forward at 60 mi/hr, someone standing on the side of the tracks will see the ball moving at 120 mi/hr, because the speed of the train and the ball add together. If he and the catcher switch places, he’s now throwing the ball at -60 mi/hr and the ball is now stationary as far as the guy by the side of the tracks is concerned: +60 mi/hr plus -60 mi/hr = zero.

OK, I’ve used a very limited situation to make a couple of points, but it’s not very interesting in the real world. What about two or even three dimensions?

I’m going to do what everyone else does when explaining velocity in two dimensions: I’m going to use a pool table as my example. It’s the best choice I can think of, and I guess that was the best they could come up with too.

Let’s say the pool table points north-south along its length. A ball is moving directly north at 1 m/s. Another ball is moving directly east at 1 m/s. They have the same speed, but different velocities, because the direction of motion is different.

Figure 2-1
Two balls moving at one meter per second so they have the same speed,
but they are moving in different directions so they have different velocities.

Now let’s consider a different ball, a red one moving at 1 m/s exactly to the north east. If you think about it, that ball is moving north at a certain rate, and at the same time it’s moving east at a certain rate. Or to put it another way, how fast would a ball (let’s make this one pale blue) moving straight east have to move so that it’s always directly south of the diagonally-moving ball? And how fast would a (purple this time) ball moving straight north have to move so that it’s always directly west of the diagonally-moving ball?

Figure 2-2
How fast does the purple ball have to move so it’s always exactly west of the red ball, which is moving diagonally?
Similarly, how about the turquoise ball? How fast must it move on the horizontal line to stay exactly south of that red ball?

You can do this visually by drawing a diagram like this, then measuring the vertical and horizontal lines. You should get about .7 the length of the diagonal line. Since that diagonal line is 1 m/s, the horizontal and vertical lines should be .7 m/s. (The exact number is actually 1, divided by the square root of 2. That can be derived from the Pythagorean Theorem. To six places, it’s 0.707107, but you will never be able to measure quite that accurately off a drawing you made on a piece of paper.)

You can do this with any velocity, big or small, in any direction. You can break it down into a north-south component and an east-west component.

So any velocity on the pool table can be expressed with numbers, but by writing two numbers, not one. Our diagonal moving ball has a velocity of [ 0.707 north, 0.707 east ] meters per second.

That pair of numbers is enough to do the job of a speed and a direction.

The Vector

And this is what is called a vector in its mathematical form.

You can also represent a vector by picking a scale (1 inch equals 1 m/sec, for instance), and drawing an arrow with the appropriate length, pointed in the appropriate direction. We’ve already done that. You can’t compute things this way but it sure does help you visualize it. And you can get estimates by measuring off the diagram if you’re careful drawing it.

Vectors are considered equal if they have the same length (mathematicians call this the “magnitude” of the vector) and the same direction. There’s no notion built into a vector of “where it starts” and “where it ends.” We can move them around for convenience, especially on those diagrams, just so long as we don’t stretch them or rotate them.

Figure 2-3
Vectors are equal to each other if they have the same length and distance, they are not equal to each other if they are of different lengths (“magnitudes”) even if they’re in the same direction, nor are they equal to each other if they have the same magnitude but different directions.

If you think back to last time, I talked about force, mass and acceleration. F = ma. But it turns out the force is a vector. When you push on something, you’re pushing in a certain direction. Likewise, acceleration is a vector too, you’re speeding up in a certain direction. It’s customary to write vectors in bold face (or if on a blackboard, by drawing a line with a little arrowhead over the letter). So it’s actually F = ma.

Mass was not written in bold, because it takes a single number to express it; it doesn’t have direction. (Weight does. Why?) Such plain-old-number quantities are called scalars in distinction to vectors.

Returning to our current topic, velocity is abbreviated v, bold because it’s a vector. So in our diagonally moving ball example, v = [ 0.707 north, 0.707 east ] m/s.

When you take a vector and express it like this, you’ve broken it down into its north and east components. It actually doesn’t matter which two directions you use, so long as they’re perpendicular, but for now let’s stick with north and east.

Even a total distance moved can be a vector. The total distance is equal to the elapsed time, t, times the speed or velocity (depending on whether you want just the distance, or the distance and direction). d = vt.

What happens when you multiply a vector by a scalar, as shown here? What you do on a diagram, is make the arrow that much longer or shorter. Mathematically, you go to each component of the vector and multiply each one by the scalar. In the case of the diagonal moving ball, you have:

d = 5s [0.707, 0.707]m/s = [3.535, 3.535]m. This is how far the ball has gone, relative to where you first started watching it five seconds before. (And it would go right off the pool table, too, if not for the bumpers. More on that later.)

Mathematicians like to do things as generically as possible. So they will write vectors in terms of x and y, rather than north and south. That means they’re not really wedded to any particular orientation. Remember I said it didn’t matter which directions you used, so long as they were at right angles to each other. For convenience when they draw diagrams, the x direction is to the right, and the y direction is upward, the y axis being 90 degrees counterclockwise from the x axis.

You can do more to vectors than just multiply them by a scalar. They can be added together, provided they’re in the same units. (No fair adding speed to force!) This also means they can be subtracted.

Of course when dealing with pure mathematics (as opposed to mathematics applied to physics), generally units are not a concern. Like in the following example.

On a diagram, take your first vector, whatever it is, and then put your second vector so that its tail is right at the head of the first vector. Then draw a new vector from the tail of the first vector to the head of the second vector. That’s the sum of the two vectors. Mathematically, you add each individual element. So [ 3, 4 ] + [ -1, 6 ] = [ 3-1, 4+6 ] = [2, 10].

Figure 2-4
Vector addition. The two black vectors add up to the red one; vectors must be placed “head to tail” to add them pictorially.

Conservation of Velocity?

So now let’s go back to the pool table, make the scenario slightly more complicated and see what we can use this whiz-bang vector thing to figure out.

This is pool, after all, balls are supposed to hit other balls. So, if we have a cue ball moving along in the x direction at, say, 1 m/s…or more rigorously [ 1.0, 0.0 ] m/s, and it hits another billiard ball head on, what happens? Well, the cue ball hits the other ball. Then the cue ball stops, and the second ball continues on along the x direction, also at 1 meters per second.

Figure 2-5
Two billiard balls, head on collision between a moving and a standing ball.

It’s as if the velocity transferred from the cue ball to the other ball, perfectly. So, is it possible we’re on the track of another conservation law, conservation of velocity?

Let’s do a little more investigation. For starters, consider a glancing blow. Let’s have the cue ball moving at 1 m/s in the x direction (ahem) v = [1.0, 0] m/s, and hit the other ball quite a bit off from head on, as shown below.

Figure 2-6
Billiard balls, an off center collision. This time both balls move after the collision.

You’ve seen this happen often enough, you know the cue ball will, in this case, continue moving, up and to the right. And the second ball will move down and to the right. And perhaps one of the two balls moves at a steeper angle than the other. That doesn’t look very much like velocity was conserved, does it? A motion in the x direction turns into two sort-of-diagonal motions?

But actually, when you look at it a bit closer, it looks good. As you can see, we’ve broken the two vectors into their x and y components.

We started with the cue ball moving at [1, 0]m/s, and the other ball (not) moving at [0, 0]m/s. Afterwards, the cue ball is moving at [0.750, 0.433]m/s and the other ball is moving at [0.250, -0.433]m/s.

If velocity is conserved, the sum of the velocities before must equal the sum of the velocities afterwards. These are vectors, and I already told you how to add vectors. So let’s do some addition:

Before: Cue ball [1, 0]m/s + Other ball [0, 0]m/s = [1, 0]m/s.

After: [0.750, 0.433]m/sec + [0.250, -0.433] = [1, 0] m/s.

So it does look like velocity is conserved. Yes, here I could have just made up the numbers to make it work out, but the fact of the matter is in real life, these billiard ball examples really do work out like this.

(And, since I did contrive this scenario, the direction of the cue ball is 30 degrees “up” from the x axis, and its speed is 0.866 m/s. The other ball is moving “down” at a 60 degree angle, at a speed of 0.5 m/s. Those who took some trigonometry might remember there’s something special about 30 and 60 degree angles and the square root of 3, divided by 2.)

A pool player will have played so many games of pool that he knows this behavior in his gut; he knows exactly where to hit the other ball with the cue ball to get the angle he wants, to send that other ball into the corner pocket.

But if it’s a conservation law, it has to hold all of the time, not just in billiards scenarios. And this one doesn’t hold all of the time in billiards, much less in the “real world.”

Nope, No Conservation of Velocity

What happens when a ball hits the bumper? If it hits the bumper head on at 1 m/s, it bounces back at 1 m/s, in the opposite direction. In other words, whatever the vector was before, it’s now a vector in the opposite direction. That’s not conservation!! (And the pool player knows this one too, of course.)

Also, not quite within the realm of billiards, what if the balls are of different weights…er, masses? You already know from your own personal life what will happen. Hit a pool ball with a cannonball and the pool ball will go rocketing away, much faster than the cannonball was moving, and the cannon ball will slow down the tiniest but not stop moving. Reverse the process, hitting the cannonball with the cue ball, and it will barely budge, but the cue ball will bounce back the way it came.

If you want to mess with a pool player, randomize the masses of the balls. Because normally all of the balls have exactly the same mass, at least as close as the manufacturer can make it. In real life very few objects have the same masses. As soon as the masses are different the tidy behavior we illustrated above goes right out the window and the player can’t predict what will happen.

So if you do some experimenting, it seems like what might be getting conserved is not velocity, but something that is the product of mass times velocity. You have to add the mass times velocity, before and after, and that will be conserved. A heavy object will move less under the same impetus from some other object, than a light one would. If mass goes up, velocity goes down to compensate, and vice versa.

Momentum

That product of mass times velocity is known as momentum. And it’s a scalar times a vector, so it’s a vector, too. And for some reason, they chose to symbolize it with p. (They didn’t use m because m is mass, but why did they pick p instead of q or u or…?). p = mv. And if m is in kilograms, and velocity is in meters per second, we can define the momentum as being in kilogram meters per second, kg•m/sec. That way we can avoid the use of a fudge factor, since the units are already consistent with each other. There is, unfortunately, no named unit of momentum like there is with force (the Newton), so “kilogram meter per second” it is.

OK, that takes care of the unequal masses behaving oddly, but what about a ball rebounding off one of the bumpers?

Actually, what’s happening there is that the ball is striking a much more massive object–the pool table. And the pool table is firmly fixed to the entire planet, if nothing else by friction.

So the entire Earth, it turns out, is reacting to that ball hitting the bumper, and picking up motion in that direction, but the earth is so massive that the motion is very, very small. In fact, in order to make the ball rebound, the momentum of the ball is changing by twice its prior value. If the mass of the ball is b, and it was moving at 1 m/s in the x direction before, its momentum was [ b, 0 ]kg•m/s before, and afterwards its moving in the opposite direction with a momentum of [ -b, 0 ]kg•m/s. Net change in momentum is [ -2b, 0 ]kg•m/s. The earth has to make up this change by gaining [ 2b, 0] kg•m/s. But the earth’s mass is much, much, much more than b, so the velocity imparted by the ball to the earth is microscopic. If one goes up the other has to come down to compensate.

One could complain that since we can’t measure the earth’s “rebound” in this case, maybe it isn’t rebounding. But the absence of evidence (i.e., the failure to be able to measure it) isn’t the same as the evidence of absence (i.e., evidence the earth doesn’t actually rebound when the ball hits the bumper). If we had a way of measuring the earth’s rebound that was sensitive enough to show what we expect based on theory, and it didn’t show that change, then we’d have evidence that momentum isn’t conserved. But if we know our measuring is inaccurate enough that we can’t see it even if it’s there, then not seeing it doesn’t mean anything, one way or the other.

Conservation of Momentum

Since this is a part of the story of where physics was in 1895, I’ll put it out, here, that as of that time, no exception was known. Every time we could measure things, momentum was conserved. It was considered a solid part of physics.

Because a vector consists of two components, and the addition rules keep the two components separately, you could treat the conservation of momentum as if it were two separate laws, conservation of momentum in the x direction, and conservation of momentum in the y direction. No one actually does this, but from a bookkeeping standpoint it’s definitely twice as much time with the ledger as conservation of mass is.

And, Oh By The Way…vectors can be three dimensional, too! It’s then a triple number, and the new axis is the z axis, perpendicular to both the x and y axes. The three edges of a cube that meet at the corner are a good representation of this.

Rockets and Guns

Now for an application. How does a rocket work? It works entirely through momentum. Let’s say the rocket’s mass is a thousand kilograms (one metric ton or “tonne”), including the fuel it has on board. And let’s furthermore imagine that it’s out in space somewhere.

A rocket engine works by shooting matter–burnt rocket fuel, to be specific–out the nozzle at very high velocity.

So if the rocket burns one kilogram of fuel plus oxidizer, and shoots the combustion product out the nozzle at 4000 m/s, what happens?

Let’s do this in one dimension for simplicity. The direction the rocket is pointed is positive. And we’re moving along with it, so it looks stationary to us. The rocket, including the fuel, has a momentum of zero.

The momentum of the rocket fuel after it has been burned is 1kg • -4000m/sec. (Negative because the rocket is blowing the exhaust out behind it, the nose points in the positive direction, the nozzle points in the negative direction.

If momentum is conserved, the rocket must now also have a momentumm, this time of +4000 kg•m/s. The rocket has a mass of 1000 kg, so that works out to the rocket now moving at 4 m/s in the forward direction.

So if we want another 4 m/s, burn another kilogram of fuel and oxidizer, right?

Good logic, but there’s a complication here. Because the rocket burned 1 kg of its own mass to get to this point, and now it masses 999 kg, So another kilogram of fuel, adding 2000 kg•m/s to the rocket’s momentum, will actually add slighly more than 4 m/s, precisely 4000/999 m/s, in fact.

For that matter, if you think about it, the mass of the rocket was declining while we did that first burn, so we must have gained a tiny bit more than 4 m/s even the first time around.

That’s quite true, actually, and the real formula for how much velocity a rocket gains by burning some amount of fuel is a bit more complex. But the takeaway is that even in following the other formula, the rocket and its burnt fuel are abiding by the conservation of momentum; in fact it relies on it to operate.

(If you’ve ever heard astronauts, or NASA types, talking about “delta vee”, that’s a reference to the total change in velocity given how much fuel is left, or alternatively, they’re talking about the total change in velocity for a specific maneuver, because that will be equivalent to a cost in fuel for that rocket, with its current mass.)

How about firing a gun? It’s sort of the flip side of a rocket. With a rocket the goal is to make the big thing move, and flinging the fuel out as fast as possible is a means to that end. With a gun, the goal is to make the little thing (the bullet) move, and the gun kicking in the opposite direction is the price paid.

Why does the muzzle flip up on a handgun? Shouldn’t it go straight back, instead of up? It would, except that the line of the barrel does not go through the gun’s center of mass, so there’s a bit of torque there, that causes the whole gun to rotate. If you grip it solidly enough, it kicks your arm up too. Tense up your arm and the entire weight of your body resists the torque and you don’t move much. (Torque, by the way, is another concept that beginning physics studies…)

These particular scenarios are also vivid illustrations of Newton’s third law: for every action, there is an equal but opposite reaction.

This is actually just another way of stating the conservation of momentum. And the first person to put forward the observation that momentum seemed to be conserved was John Wallis in 1671. Newton put forward his three laws in 1687.

Vector fun.

OK, here’s another application of stuff we’ve learned today. You have two identical cannonballs. You drop one. (Hopefully not on your foot.) At the same instant, the other is fired out of a cannon, perfectly horizontally. (Hopefully at a deserving target.) Oh, and you do your drop at the same height as the cannon’s muzzle.

If you’re on perfectly flat ground, which cannonball hits the ground first?

They hit at the same time.

Look at it from a vector standpoint. X is the direction the cannon fires. Y is straight up.

The dropped cannonball starts the experiment with v=[0,0]m/s. The fired cannonball, on the other hand, starts out with v=[200, 0]m/s. I just made that x number up; it doesn’t matter what it is as you’ll see in a moment. (Well, you’ll see it if if I did my job right, today.)

The force of gravity imparts an acceleration of –9.8 m/s² in the y direction, i.e., straight down.

This acceleration can only affect the y component of the velocity vectors, since it’s purely in that direction. And in the y direction, both cannonballs are stationary and in the same place when the experiment starts.

Thus, they both have the same fall, and they will both hit at the same time. It doesn’t matter how fast one of them is moving sideways! And in fact they don’t even need to be the same weight.

I’ve seen demos of this principle done where steel ball bearings are used, in a special little gizmo that drops one the same time a spring shoots the other one out horizontally. You only hear one clack as both balls hit at the same time.

Can’t get the drift.

Last time around, I highlighted what was, in 1895, a standing mystery. Gravitation seemed to work, except they couldn’t figure out what was going on with Mercury’s orbit about the sun. A similar problem with Uranus had led to the discovery of Neptune, so it seemed as if there must be some planet closer to the sun than Mercury, lost in the Sun’s glare, perturbing its orbit. Despite the best efforts of astronomers, that planet (already pre-named Vulcan) had never been found.

This time I’m going to highlight a different little issue.

I mentioned before that velocities were additive, right? A ball thrown by a pitcher on board a moving train ends up moving, relative to the outside observer, faster or slower than the pitcher threw it, by the speed of the train, depending on the direction of the throw.

Can we do this with other things? Sound, for instance, travels at a specific speed (one which varies depending on temperature, humidity, pressure, whether His Fraudulency is on or off his meds, and a host of other factors, but still, a speed that will remain constant until one of these factors changes). Trains have a nice source of sound on them, the whistle (or today the horn). So how fast is the sound travelling in front of the train, and how fast is it travelling behind the train? Measurements from the ground show that they are travelling at the same speed, not different speeds. (They also show that in front of the train the pitch is higher, but that effect is a different rabbit hole. Some other time, perhaps. No, some other time, definitely.) What’s going on here?

It turns out that sound is a wave that travels through a medium, air. It’s going to move at a certain speed relative to the air.

The train is moving, the air is not (unless it’s Wyoming). Thus the sound wave travels the same speed in all direction from the train’s whistle (horn), as seen from someone on the ground on a breezeless day. If some bored passenger on the train were to measure the speed of sound (assuming they’d let him climb around on top of the train in the first place), he’d see the sound move slower, relative to the train, when measured from in front of the whistle, at a normal speed to the side of the whistle, and faster behind the whistle. He could even figure out how fast the train was going by taking the difference between his “in back of” reading and his “in front of” reading and dividing by two. If he were really ignorant of how trains move, he could even prove it wasn’t moving sideways, but rather forward, this way.

Looking at light, we had originally thought it was instantaneous, it was so doggone fast. But then…well, remember Jupiter’s moons from last time? We could predict their motions once we knew Newton’s law of gravitation, actually we could do so from Kepler’s laws of planetary motion, known earlier. (We didn’t even really need to know the mass or distance to Jupiter to be able to do that.) Well, there was one little anomaly. We could predict the motions all right, but the motions were about eight minutes and twenty seconds early when we were closest to Jupiter, and eight minutes and twenty seconds late when we were farthest from Jupiter.

A little thought and someone realized, that the difference was due to the speed of light not being infinite. What we see now going on around Jupiter actually happened at some time in the past, when the light left Jupiter. It then took some amount of time for the light to get here.

The eight minutes and twenty seconds, really in total a 16 minutes and 40 seconds difference, reflect the amount of time it took light to span the entire width of the earth’s orbit about the sun, because it has to cover that much additional distance when we are farther away, versus closer, to Jupiter. (This works out to about a thousand seconds, by the way, a neat coincidence.)

We didn’t know how big the earth’s orbit was, and wouldn’t until the 1760s. Before that we just knew however big it was, light took a thousand seconds to cross it, you could even call it a distance of one thousand light seconds. But once we discovered that the earth’s orbital diameter is roughly 300,000,000 kilometers, we now knew light moved at about 300,000 kilometers per second (186,000 miles per second). This was another product of all that work measuring the solar system that I totally forgot about when writing that article (which is OK, because it fits better here anyway).

Light was, and is, believed to be a wave. So, presumably it goes through a medium, just like sound does. But it must be an otherwise intangible medium, or planet earth would be suffering drag plowing through it. Only light could “feel” that medium. We knew it had to be there, and so we gave it a name: It was the ether.

We might not be able to feel the ether, but we sure as heck ought to be able to measure the Earth’s velocity through it, the same way as the man on the train: by measuring the speed of light in different directions here on Earth.

Measuring the speed of light in a laboratory was difficult to do accurately in the mid 1800s, but we could be much more precise by comparing two different beams of light in two different directions, and seeing what the difference in their speed is.

Michelson and Morley tried this in 1887. They found no difference in the speed of light no matter which way they measured.

Well, it’s possible that at that point in our orbit, we just happened to be stationary with respect to the ether. But that couldn’t be true a couple of months later, because the earth would at the very least be orbiting in a different direction, so they kept trying.

Others have tried too, with much better equipment.

No difference. Ever. No one has ever “got the drift.”

What’s going on here? Well, that, like Vulcan, was a mystery as 1895 dawned.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·05·01 Joe Biden Didn’t Win Thread

His Fraudulency

One can hope that all is not as it seems.

I’d love to feast on that crow.

Physics?

Part 1 was last week. I intended to do Part 2 this week, but both of my drafts are an utter mess. I’m going to keep plugging away at it, though, so hopefully next week.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

(Paper) Spot Prices

Last week:

Gold $1778.20
Silver $26.07
Platinum $1236.00
Palladium $2914.00
Rhodium $28,000.00

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $1768.60
Silver $25.97
Platinum $1205.00
Palladium $2996.00
Rhodium $29,000.00

Of these, palladium continues its steady climb. In fact, on Thursday it had closed at $3012, above three thousand dollars for at least the second time in the last week.

I did, long, long ago, buy some palladium, not a huge amount. (But I can drop it on my foot. I won’t hurt if I do so, because, like I said, not a huge amount.) I even told the guy I was buying it because it had gone over 900 bucks earlier (which at the time was higher than gold had ever been), maybe it would do so again. He scoffed, and explained that was due to a temporary supply interruption from Russia, unlikely to ever happen again. But now, it’s worth well over ten times what I paid for it. In fairness, I had to hold onto it for over 20 years for it to finally do what I wanted it to do, so this isn’t the short of thing that is a “short term” play.

I knew someone who, about the same time, wanted to find a way to get into rhodium, but back then there was no such thing as a rhodium one ounce bar. I don’t know if he managed to find a way to do it, but if he did, he has done very, very well, even if it took a couple of decades for it to finally move.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·04·24 Joe Biden Didn’t Win Daily Thread

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot (i.e., paper) Prices

Last week:

Gold $1777.50
Silver $26.05
Platinum $1207.00
Palladium $2834.00
Rhodium $28,200.00

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $1778.20
Silver $26.07
Platinum $1236.00
Palladium $2914.00
Rhodium $28,000.00

Unfortunately, when looking at the prices only on Friday, you lose some things. It looks like gold has barely moved, but the fact of the matter is, it almost blooped up above $1800 earlier in the week. A far cry from the situation just a few weeks ago when it would drop below $1700 and then popped back up again, two or three times.

To really get a feel for what is going on, you should look at a chart.

Here is what gold has done this past year:

http://www.dailymetalprice.com/metalpricecharts.php?c=au&u=oz&d=240

The price is moving up and down, but the overall trend is down, imagine a series of sawtooths (sawteeth?). And if you look at the recent rise, it’s still consistent with just being an upward movement in the overall down trend; you can sort of eyeball a straight line through all those peaks, sloping down and to the right, and the price of gold hasn’t broken through that line, not yet it hasn’t. A trader would likely expect it to reverse and drop again.

Palladium on the other hand, is in a slow upward trend, again as seen in a graph for the past year:

http://www.dailymetalprice.com/metalpricecharts.php?c=pd&u=oz&d=240

And so I would expect it to continue to climb, for now. Here’s rhodium:

http://www.dailymetalprice.com/metalpricecharts.php?c=rh&u=oz&d=240

Note that it has gone from below $10,000 to almost $30,000 just since last June. Also note at the far right the price is moving up and down, but the height of the oscillations is decreasing. This may be what the technical traders call a “flag,” if so when it reaches its “point” the commodity often breaks out, either up or down, in a big way.

Here’s iridium:

http://www.dailymetalprice.com/metalpricecharts.php?c=ir&u=oz&d=240

And it probably shows the most stark behavior. Dead flat for months, then suddenly it starts climbing, and climbing, and climbing! That line almost looks like the profile of the Grand Canyon, in fact, complete with the vertical faces and then lines sloping upward to the next vertical face.

Mass (Part I of a Long Series)

Introduction

Having run out of precious metals to babble about, I’m going to change tacks. If you’ve been here a while, you might remember two postings I did on stars. These were independent posts, having nothing to do with politics (poly = many, ticks = blood sucking bugs) and at least some people enjoyed them. I wanted to go to the opposite end of the scale and talk about a certain sub-atomic particle, but then I realized that the best way to do that would be a very, very, very long post. (And yes, it’s a subatomic particle, but it has a lot to do with stars.) A huge part of it would be explaining where physics stood in 1895, and how four discoveries in the next four years basically overturned things, and eventually led to that subatomic particle, the real star (ahem) of the whole series.

So I decided to break this story up into pieces. And this is the first of those pieces.

Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off. I use 9.8, below, for a number that’s actually closer to 9.80665, for instance, similarly for the number 32.

OK so without further ado, mass.

What Mass Is, and Isn’t

Mass is not the same thing as weight, at least not when scientists are using the terms.

But the distinction between mass and weight didn’t become clear until Isaac Newton came along. He tried to imagine what objects would behave like if there were no gravity, and no friction. And he realized that an object under those circumstances would stay at rest unless a force acted on it, or, if were already moving, would continue to move in the same direction at the same speed, unless a force acted on it. It has inertia. But that doesn’t match what we actually see. You let go of an object that’s not on the ground, it falls (or if it’s a balloon, it might rise). An object that’s moving on a flat surface slows down and stops.

But the reason why we see things fall faster and faster, is that gravity exerts a force on them, a downward force, and the reason things moving horizontally slow down is friction, and that, too is a force.

For clarity, we have to ignore friction. Imagine these objects are wet ice on a hockey rink–or cars sliding on ice (yikes!). Or air hockey pucks. There’s still some friction in all of these cases, but not a whole lot. You can imagine, after watching these sorts of things, what it would be like with no friction.

Largely building upon what Galileo discovered (when he wasn’t looking through a telescope), Newton essentially defined the concept of inertia. It’s basically the resistance of an object to being shoved. And mass is essentially a measure of that. If object A is twice as massive as object B, it’s twice as hard to shove around and get the same effect. You need to exert twice as much force.

On the other hand, if you stick with the same object, and apply twice as much force, it reacts twice as much.

You can state this a little more precisely as, acceleration, a, is proportional to the force, F, and inversely proportional to the mass, m. You can increase or decrease any of the three items, decrease or increase one of the other two, and you will see the third item increase or decrease exactly in proportion.

Or to be even more concise, you can write the following:

a ∝ F/m.

That little Jesus fish like thing means “is proportional to” and basically, it means that if you double one side, you double the other side, but they’re not equal.

You can rearrange to get:

F ∝ ma.

And this is the form you usually see this in, it’s Newton’s second law of motion. Well almost. There’s something we can do to get rid of that Jesus fishy thing and replace it with an equals sign. More on that shortly.

Mass is considered to be the ultimate measure of “how much matter” is in an object. Twice as much matter, will have twice as much inertia. And some object, say one of the big weights off of a weightlifting set, will have the same inertia even on the moon.

But the weight of the objects will change on the Moon, because weight is actually force. And the Moon’s gravity will pull on the same objects, with less force than on Earth.

The kilogram is actually a unit of mass. A chunk of metal massing a kilogram (think of it as a one kilogram gold bar if that will put a smile on your face) will still mass a kilogram on the moon, pick it up and swing it around, you will feel the same tugs as you would feel on earth, because now you are playing with its inertia, which doesn’t change–it will take the same force to keep the bar from flying out of your hand as it did on Earth.

But pounds are (usually) a unit of force. That kilogram of gold will weigh about 2.2 pounds here on Earth. That means that the earth’s gravity pulls on it with that amount of force. But take it to the moon, and it weighs about 5.9 ounces, that’s how much force the moon exerts on that one kilogram mass.

[Or–let’s be frank here–for me, and for most of you, it weighs exactly zero both on Earth and the Moon because your kilogram bar of gold doesn’t exist at all except in your dreams. Oh, OK, never mind, forget I said this and return to smiling.]

The one force we can’t get away from in our daily is gravity, and as such in the English system a lot of things are defined with respect to the amount of gravity Earth has. But when you’re doing engineering you have to deal with a lot of forces–the force exerted by a pile driver, the thrust of a jet engine, and so on. So you need a unit of force and a unit of mass, so you can figure out how much your masses will respond to your forces, or alternatively, how much force you’ll have to exert to make that mass move the way you want it to.

The metric system, which starts with unit of mass, has to derive a unit of force, and the English system which starts with a unit of force, has to derive a unit of mass. Metric invented a unit of force called the Newton–the amount of force needed to accelerate a kilogram, one meter per second, for every second it’s applied, and yes, it’s named after Sir Isaac. And the English system retro-invented the slug–it’s the amount of mass that, when acted upon by one pound of force, will accelerate one foot per second, every second.

Once you’ve defined your units, you can change that proportionality constant to an equals sign. But you may need a fudge factor, which I will call k. F = kma. (And yes, Biden can kma.) In metric, as long as you stick to meters, kilograms, and meters per second squared, the fudge factor is 1. The Newton was deliberately defined that way. And in the English system, as long as you stick to feet, slugs, and feet per second squared, the fudge factor is also 1. 1 will disappear if it’s in an algebraic multiplication, so now we’re dealing with

F = ma

Drop a kilogram of gold–it will accelerate at 9.8 meters per second per second, a = 9.8, and m is one. Plug it into the formula above. That means it’s being acted on by a force of 9.8 newtons.

Galileo showed that heaver objects fall at exactly the same rate as lighter ones (once you account for air resistance, which is a force and partially cancels out gravity). So a two kilogram mass of gold, falling at the same rate, which we call g, gives you F = 2 x 9.8 = 19.6 Newtons.

Switch to the English system now. Drop a pound of something else–bananas, say–it will accelerate at 32 feet per second, every second. (That’s the English equivalent of 9.8 meters per second per second…we’re just using a different measuring stick.) But this time we have a weight, not a mass, F, and we have a and are looking for m, so we need to do a bit of beginner’s algebra and come up with:

m = F/a

But this time F is 1 pound, and a is 32 feet per second squared. So our mass is 1/32. And indeed, if our answer is supposed to be in slugs, that’s the right answer. A slug, as it turns out, weighs 32 pounds here on earth, and 1/32 of a slug weighs one pound.

Engineers find it so useful to have a unit of mass, the ones working in the English system (poor sods) actually invented a “pound mass,” the mass of something that weighs a pound here on earth. But when they use the “pound mass” in their formulas they have to put a fudge factor of 32 in. With mass in pound mass, the formula becomes

m = 32 F/a

Or rearranging to the usual form

F = ma / 32

A pound mass will respond to a force 32 times as much as a slug would to the same force, as you can see when you solve for the acceleration (response), a = 32 Fm. Failure to properly account for this has doomed more than one rocket. Metric is cleaner, a kilogram is mass, and only mass.

I got my STEM education entirely in metric, that’s what I’m comfortable with, that’s what I’m going to use from here on out.

OK, so mass and weight are different. How do you measure them? If they are different things, you need different methods to measure them.

A force can be measured with a spring. Your typical bathroom scale, or your kitchen scale, will have a spring inside; the amount the spring is compressed by the stuff you put on the scale is a measure of the force exerted on the spring. Drag your kilogram of gold to the moon and bring your scale with it, it will push on the spring less and therefore weigh less.

A mass is best measured by a balance scale. Your doctor’s scale, for instance, is a balance scale. Take it to the moon, and if it read 100 kg on earth, it will read 100 kg on the moon.

But it’s probably marked off in pounds. If you weighed a hundred pounds on earth…that scale will read 100 pounds on the moon. It’s actually measuring your mass but is calibrated in pounds actually pounds mass. So it only looks like it’s measuring your weight.

A kilogram (mass) weighs 2.2 pounds on earth, the object that exerts a force of 2.2 pounds on earth, has a mass of one kilogram. That 2.2 will change on every different planet, however, since most of us never leave earth, we simply think of a kilogram as equaling or being the same as 2.2 pounds, when it really isn’t. It isn’t the same thing, any more than a gallon is the same as 8.33 pounds. (It weighs that much if it’s water and we’re on earth, but that doesn’t make a gallon the same thing as 8.33 pounds in any fundamental sense.)

With me still? I hope so.

Conservation of Mass

OK, I’ve shown you Newton’s Second Law by way of introducing you to the distinction between weight and mass. It’s called a “Law” not because some politician decreed it, but because the universe works this way.

F = ma

Always.

And when you have to use a fudge factor, the fudge factor is a constant. It’s a constant 1 in the case of metric and English slugs.

One could ask what would happen if the fudge factor were to change, and the answer is a bit surprising. Since the Newton is defined as being the force necessary to accelerate a kilogram at one meter per second per second, if it suddenly, tomorrow, took twice as much force to do that, the Newton would simply get twice as big.

Since it’s awkward having your units of measure change (for exactly the same reason that inflation sucks), the fact that scientists set things up that way should be evidence enough that they are sure the fudge factor never changes.

How do we know that? It is an induction, not a deduction. It has always been true, we assume it’s just the way the universe works, until we find an exception, and believe me, people are always looking for the exception. And also for just outright blatant violation of the rule; such as objects suddenly and inexplicably changing their velocity. That would be an a without an F, or perhaps the m taking a vacation and reducing to almost nothing momentarily.

Our whole view of the universe wouldn’t make sense if Newton’s second law weren’t true. Car collisions on icy roads, air hockey…if someone made an animated movie where this rule were blatantly violated, it would look fake to us. Of course if the movie were almost spot on, with maybe the fudge factor changing by 1 percent at random, we’d have a hard time seeing it, but this has been measured in laboratories, and it’s always true. And the fudge factor doesn’t change.

One other thing turns out to be true, at least as of 1895. Mass never disappears into nothing, and it never appears from nowhere, either.

Sure, the mass of an object can change. It could decrease. But that mass always goes somewhere else, it never gets destroyed. Or similarly, if the mass of an object increases, that mass came from somewhere else.

This is one of those realizations that turned science into a form of bookkeeping. The books have to balance, the mass in has to equal the mass out.

Set a two kilogram log on fire. Weigh the ashes afterwards, they mass out to maybe 600 grams. Did the other 1400 grams just disappear? Nope. It can’t, it’s not allowed to. So that tells the scientists they didn’t account for something. In this case, they didn’t capture and weigh the smoke and the carbon dioxide given off by the burning log (whilst upsetting leftists). So if you add that in, are you okay?

Nope, because now the mass after is more than the mass before. That’s not allowed either; you can go back to the bench and re-run the experiment.

This time, count not just the wood, but also the oxygen used to burn the wood.

Once you do that, your mass before matches your mass after. Life is good.

The books balance.

And this was another thing that (as of 1895) was considered to be always true. Every time it had been tested, it was true. And a test isn’t just an explicit lab exercise like I just described, but literally everything done in a lab implicitly follows this rule.

In this case simple arithmetic is enough to do the bookkeeping. And nothing of negative mass has ever been seen, so you will see addition and subtraction, but never a negative result. Real accountants would find this dead easy. The trick, of course, is to account for everything, and measure carefully.

Gravity

There is one other thing about mass, though, that was (and still is) an important feature of the universe. And that is gravitation. I’ve mostly talked about gravity as something that exerts a force on a mass, so far, but I’ve not mentioned yet that mass actually exerts gravity. Every mass, exerts a force on every other mass. If you double the mass of the object, it exerts twice as much force. If you double the distance between the objects, however, you divide the force by 4. This is the square of the distance, and you’re dividing by it, so it’s called an inverse square relation. But one more thing. If you double the mass of the other object, the force you exert on it doubles too, and it responds with the same acceleration.

You are exerting a tiny gravitational force on the Andromeda galaxy. And vice versa. In fact, it’s the same amount of force in both directions.

The law of gravitation was also first noted by Sir Isaac Newton.

You can write this law as follows, at least as a first cut.

F = m₁ m₂ / d²

Multiply your masses together, divide by the square of the distances, and you get F.

Except, no you can’t. Meters, kilograms, seconds, and Newtons go together with F=ma, but they don’t go together in this equation. Two masses 1 kilogram each, at one meter’s distance? That equation says the force should be one Newton. It’s not. It’s a lot less. You need to plug in a fudge factor, and this one is named G. The law of gravitation properly reads

F = G m₁ m₂ / d²

And G is a very small number, because in Newton’s day you couldn’t even measure what F was. Without being able to measure F, we couldn’t figure out what G was. And for any scenario where we could measure F, we either couldn’t measure one of the masses, or d, or both. Either way, G was unmeasurable.

But even without that, Newton could see the law was good, because he could check the responses of things to earth’s gravity. An apple, and the moon.

To start this out, in fact, let’s assume we want to measure the acceleration, not the force. Both sides of the equation above are a force, dividing by the mass of one of the objects, the one we want to watch, gives:

a = G m₂ / d²

And you can substitute mass of the earth, m_e, for m₂. So the acceleration of, say, an apple dropped, is:

a = G m_e / d²

And if you’re standing on the surface of the earth, d is the radius of the earth. (You can treat the earth as if its entire mass were at the center, so long as it’s radially symmetrical (which it almost is). That’s one of many things Newton proved. He had to invent calculus to do that.)

In this particular case, we knew a, and we knew d, but we knew neither G or m_e. But we knew what their product had to be! This is called the earth’s gravitational parameter, and is usually written μ_e. (Greek letter mu, usually pronounced as “mew” in English, though logically it should be “moo.”) This is very handy, in fact, it’s so handy that even today people who work with orbital motion just use gravitational parameters; it saves them the bother of multiplying the same numbers over and over again.

a = μ_e / d²

Newton had pretty good information on how far away the moon was. He could compute how much it was accelerating as it orbits the earth (always downward, as if it were on a string being whirled around the earth), and his equation and the data matched. The moon responded to Earth’s gravitation exactly the same way as the apple did. This was the first time we had ever shown that something “up there” follows the same physical laws as something “down here.” And that’s why it’s called the universal law of gravitation.

So Newton knew the earth’s gravitational parameter, and the distance to the moon was known before his time. But what about the rest of the solar system? Well, life was rough for astronomers working out the solar system back then. Because we didn’t know the actual distance between the sun and any of the planets, nor between other planets and their moons. We did know the relative distances; we knew, for instance that Jupiter’s distance to the sun was 5.2 times that of Earth’s. Kepler had figured that out in the late 1500s. We could also see that the inverse square law worked: The acceleration Jupiter experienced was about 1/27th that of earth, though we couldn’t tell what it was because we didn’t know the scale. Newton, in fact, showed mathematically that any inverse square force will cause things to orbit in ellipses, thereby vindicating and strengthening Kepler, and using Kepler as evidence that an inverse square law was involved.

Measuring the Solar System, Massing the Earth

So astronomers didn’t know the gravitational parameter of the sun, much less G and the mass of the sun. And they didn’t know d, in this context the distance from anything to the sun, much less the earth-sun difference (but they named it: It’s an astronomical unit, and is still called that to this day). But if they could figure out what d was for Earth, they’d know it for everything else in the solar system, because we knew the proportions. And if they knew d, they could figure out the Sun’s gravitational parameter, because you can figure out the acceleration directly from d and the length of the year.

Astronomers got the first intimations of d when we were able to triangulate on Venus as it crossed between earth and the Sun, in 1761 and 1769. We could plot its motion and position on the sun’s disk from multiple places on earth, see how different it was, and determine how far away it was, just like when you move your head from side to side, a near object will move against the horizon more than a distant one will. If you measure that apparent shift, and know how much you moved your head, you can compute how far away it is. Multiple parties went to different places on earth, just to measure these transits, the more measurements the better. It was one of the first major examples of international scientific cooperation.

Similarly we now had a good number for the distance to Venus, and because we knew the proportions of the solar system, we instantly had the distance from earth to the sun. We therefore knew a, and…now we had the gravitational parameter of the sun, because it was equal to a times d².

The gravitational parameter of the sun is 333,000 times the amount of the gravitational parameter of the earth. Since both numbers are G times the mass, you can see that the sun’s mass, whatever it is, must be 333,000 times that of Earth. Whatever that is. We still didn’t know.

But even better. We now knew the exact distance to Jupiter. And we could therefore watch how far the moons of Jupiter got from it in the night sky, do a quick calculation and get their orbit sizes…and now we could figure out the gravitational parameter of Jupiter! It is 317.8 times that of the earth, so its mass is also 317.8 times ours (again, whatever that is). Saturn has moons, and we could do the same thing for it. Mars has moons too, but they hadn’t been discovered yet.

Then in 1781 the planet Uranus was discovered. And in 1787, two moons were discovered. Shazaam! We knew how many earth masses Uranus was, and six years earlier we hadn’t even known Uranus existed. And we eventually figured it out for Mars, when we finally did discover its moons a century later.

But Venus and Mercury don’t have moons, and we could only make educated guess at their masses…until the 1960s and 1970s when we sent probes to them and could see how they interacted with those planets.

One last piece of the puzzle. Henry Cavendish (1731–1810) was actually able to measure the force of gravity between two heavy lead balls in his laboratory in 1798. This was painstaking work, but he now had a situation where he knew every term in the law of gravity except for G; he had the force, the distance, and the masses. So from that he was able to compute the value of G, and (in metric) it is: 6.67 x 10^-11.

Now that we had that number, we could go back to every gravitational parameter we knew, divide by G and get the masses.

Now we knew the mass of the Earth. It’s 5.972×10²⁴ kilograms. And everything else proportionately.

We did this, but we did not have to go “out there” and weigh anything.

Problems with the Law of Gravitation?

The law of gravitation worked really, really well. We never saw anything inconsistent with it…well, almost!

When we tracked Uranus in its orbit about the sun, it was clear it was not following the law, not quite. Was something wrong with the law of gravitation? The law was so useful everywhere else, and I mean everywhere else, that it would make no sense for it to be broken here, so instead of assuming the law was broken, we figured that there was something unknown out there, pulling on Uranus. It was complicated work, but Le Verrier in France and John Couch Adams in England both did the calculations in 1845, and when they told Galle, another astronomer, one who used a telescope rather than being a theorist, where to look…well, Galle found the planet Neptune almost immediately.

Far from it being a problem for the theory of gravitation, the discrepancy with Uranus’ orbital motion turned into a triumph, for the theory of gravity had been used to discover a planet, and had predicted it so well that it took someone who knew where to look less than an hour to find it.

That gives you a really strong feeling that this is the truth!

But I mentioned two problems. What was the other one?

The other was the orbit of Mercury. It’s an elliptical orbit, and if Mercury and the Sun were alone in the universe, that ellipse would never, ever move. But it does move, the long axis shifts 574 arc seconds every century. And of course Mercury and the Sun aren’t alone in the universe. So what we should be able to see is that the planets–and the sun’s slight oblateness–explain Mercury’s orbit precessing.

But when you add up all those effects, there’s still a discrepancy. They don’t add up. There’s still 43 arcsecond per century left over. And this bothered scientists.

But really, this probably isn’t a problem. We know what the answer has to be. There’s an unknown planet pulling on Mercury, one so close to the sun we just couldn’t see it in all the glare. The same Le Verrier that predicted Neptune predicted this planet. We even gave it a name, Vulcan; a perfect name because he was the Roman god of the forge and it gets hot near forges and near the Sun. But despite what you may have heard, scientists usually want to square things away, they want to see that planet, then they’ll be confident they know why Mercury is misbehaving.

But Vulcan was never found, and in 1895, it remained an open question. They expected to find it, they just hadn’t, yet. In truth, it really would be hard to see something like that; it can only be done during solar eclipses.

Conclusion

Well, this turned out to be pretty long. And maybe hard to follow (I hope not). But as I wrote it I realized how much “hung off” the concept of mass, and the law of gravitation, and how much we were able to learn about the solar system and our own Earth, each bit of knowledge building on the prior, with theory used as a framework. And you saw some limitations…we could only estimate the mass of bodies with no moons. This wasn’t even where I wanted to go with this, but it was too good to pass up. (Next week we continue towards our final destination.)

But hopefully you saw some notion of how science is supposed to function. It’s full of humans with their own foibles, of course, but in the end the truth does out. It’s nice when you can use a theory to predict something unexpected; it gives you a very warm fuzzy sense that the theory is correct. But at the same time, there are implicit assumptions; that the generalizations we see will continue to hold true. Sometimes we discover otherwise, and have to adjust; usually when that happens it turns out that the generalization was true under certain circumstances and is still useful, under those circumstances, but that you have to scrap it under others. (At the risk of a spoiler, you’ll see that Newtonian gravity is one of those cases.)

And in so many cases, if we seem to see far, it is because we stand on the shoulders of giants, the men who preceded us, and they stand on the shoulders of the men who preceded them. None of this could happen if we weren’t willing to use information gathered by others and build on it, and in turn that’s a testament to the power of being able to write things down so that knowledge outlives us.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·04·17 Joe Biden Didn’t Win Daily Thread

Last Precious Metal Post

I left the best (by many measures) for last.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices

All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend).

Last week:

Gold $1745.20
Silver $25.35
Platinum $1205.00
Palladium $2700.00
Rhodium $27,000.00

This week:

Gold $1777.50
Silver $26.05
Platinum $1207.00
Palladium $2834.00
Rhodium $28,200.00

SIlver and platinum have been pretty steady. Palladium continues steadily climbing. Rhodium continues to bounce around like a yo yo. Iridium (not shown) has moved from $6000 to $6250. And gold is actually doing fairly well, breaking out of its range on the up-side.

I will have more to say about the gold market below.

Gold

Gold is the last precious metal on our list of nine.

To summarize/review, the precious metals are numbers 44-47 in the table below (ruthenium, rhodium, palladium, and silver), followed by the group right below them, 75-79 (rhenium, osmium, iridium, platinum, and gold).

It’s a nice tight group. Why isn’t 43 (technetium) on the list? Well, largely because technetium basically doesn’t exist. It’s naturally radioactive with a two million year half life. That means however much you’ve got right now, half of it will be gone in two million years. And since it has been 4500 million years since the earth formed, it has been 2250 half lives. If the entire world had been made of solid technetium when it started, that would have been 6 x 10²⁴ kilograms of Tc. And since ten half lives is enough to reduce the amount to 1/1024 {a number which we should name after Fauxcahontas) of what it was before–which we’ll round to 1/1000th, it would only take eighty half lives to be left with six kilograms of technetium. From the weight of the earth down to six kilograms in 160 million years; you can probably guess how much is left after the remaining 2,170 remaining half lives: zero, zilch, nada, nichevo, nichts. The last atom would likely be gone after only about another 200 million years. (99 grams of Tc-99 consists of 6 x 10²³ atoms of the stuff, that’s 1/60th of the 6 kilograms. You’ll notice how similar that number is to the number of kilograms the earth masses…so basically, just repeat the same time interval as before and it’s down to a handful of atoms, shortly after that, it’s all gone.)

We can make technetium ourselves (and a vanishingly small amount exists from uranium atoms fissioning in nature, but these aren’t left over from the formation of the earth). When you pile enough of it together to be visible…it’s a gray metal, just like all of its neighbors. I imagine if it weren’t radioactive, it’d be a useful alloy metal, perhaps a bit pricey, like silver. Or maybe not; I’m basing that last bit on the fact that rhenium (75) is a precious metal, and that’s because rhenium has no natural ores. But if technetium were around, it might have ores and rhenium could piggyback on it, just like hafnium (72) piggybacks on zirconium (40). So who knows?

But the larger point is, for a metal to be a precious metal, it first has to actually exist. So technetium, though it looks like it should be part of the precious metal “block” of the periodic table…isn’t. In both senses of that word.

But back to gold (79).

Gold has been known for thousands of years. Perhaps longer. And that’s because it sometimes shows up as a nugget. It didn’t have to be smelted to be discovered, unlike (say) iron, which never shows up as a native element on earth, though sometimes our ancestors got a free sample from a meteorite.

So our distant ancestors might well have found gold before they discovered any other metal. [Of the ones that had to come out of ores, copper is probably easiest to obtain. Besides being rarely (but not quite never) found native, some of its ores will release the copper if you heat them over an ordinary fire.]

Ancient Egypt used plenty of gold. In fact it was more common there than silver was; as near as we can tell, three ounces of gold were required to buy one ounce of silver in Ancient Egypt, oh say 2000 BCE. No, that’s not a typo. Egypt simply didn’t have much silver in it, and they didn’t know it was more common elsewhere. Certainly they figured that out as civilization spread throughout the Mediterranean and Near East and they learned more about the rest of the world.

Gold is heavy (dense)–it was the densest thing known back then, far more so than lead. Lead weighs almost twelve times its volume in water. Gold weighs 19.3 times its volume in water. But gold looks fantastic and lead is…meh. About the only thing you can do with lead is use it for weights. Even its use as bullets is primarily due to its weight–it has good momentum–followed by its relative softness and ease of melting and casting.

But gold can be used for jewelry, and was. Not only that, it would never tarnish nor rust nor corrode. Gold coins that have been on the bottom of the ocean for centuries still shine. So it became a symbol for purity and incorruptibility, unlike most politicians. Even modern chemistry has found few things that attack it. (This is largely true of the other precious metals as well, but they are Johnny-come-latelies in our minds. Gold got there first.)

So gold began to be prized in its own right.

Gold and silver are the only two of the nine precious metals whose main use is simply to be. They’re not valuable because of some industrial application, like the PGMs and rhenium are. They’re valuable because they are gold and silver, and their main use is to be formed into blocks and kept on a shelf somewhere.

Even back in the day when men were men and money was money, when gold was used as coins, the point of the coin was to be a certain amount of gold.

Although gold is used in jewelry, most gold today is in the form of 400 ounce bars that sit in bank vaults. I think I linked this video once before; I’m going to do it again.

The sole use of all that gold is to sit in that vault and be gold.

It has been estimated that all of the gold ever mined could fit in a cube 20 meters on a side. That’s 8000 cubic meters of gold, and each cubic meter is 19.3 tonnes. Given how vague the actual number is, we might as well round that to 20 tonnes per cubic meter, and declare that 160,000 tonnes of gold have been mined throughout all history.

A “tonne”, with the extra n and silent e, is a metric ton of 1000 kilograms, very roughly 2200 pounds. 160,000 tonnes sounds like a lot, but this is gold, which doesn’t take up very much room per tonne. it would barely fill three Olympic swimming pools.

Here’s another video. It’s mostly on the never-to-be-sufficiently-damned Federal Reserve System, but there’s a good bit in the middle about gold, and how it is traded.

https://www.youtube.com/watch?v=vTYBp8AazN8

(In fact, National Geographic has done a number of different documentaries on gold, some focusing on the lengths we go to in order to mine it, others focusing on King Tut’s treasure, and so on.)

Gold, is of course, very widely traded. It’s probably traded more than any other commodity, at least in dollar terms. And those trades are how the “spot” price I quote comes into being.

Here’s another documentary, looking more at this aspect of gold:

https://www.youtube.com/watch?v=iqjhdpQIWTs

The spot price is sometimes derisively referred to as the price of “paper gold.”

“Paper gold?” Well, yes. You’re trading paper ostensibly tied to gold in the futures market. If you want to go buy an actual ounce of gold today, and walk away from the purchase with an actual bit of heavy yellow stuff, you will pay (on Apmex.com, as of Thursday April 15 at 8:30 PM Mountain TIme…”as low as” $1,949.29 per ounce, for an American gold eagle, a randomly chosen year.

Nearly two hundred dollars more. (And if you want just one ounce it will cost you twenty dollars more. You have to buy a hundred at a time to get the $1,949.29 price. Actually, that’s not a bad small-buyer premium; it’s usually much higher.)

You can check with your local coin shop, and more than likely they will want a little bit more. This is the real price of gold, though perhaps one should average it with the price a bullion dealer is willing to pay. Unfortunately Apmex doesn’t post their “buy” price, and neither does Kitco, they want you to call and request an offer. But I strongly suspect they aren’t paying much less than this. If so, then it’s rather unusual but you can actually sell your gold for more than spot right now.

I did find one place that would sell you a 100 gram bar (a bit over three ounces) at a rate about a hundred dollars an ounce lower than that. (And they will also buy it at that price. The catch is, you can’t sell their gold back to them in less than seven days, so you assume the risk the market will move against you.) https://www.bullionstar.com/buy/product/gold-bullionstar-100g

Why is there such a big disconnect between the “paper” price and the physical price?

“Conspiracy theories” abound, and I find them more plausible than most such theories. Most state that the price is being held artificially low. (I even attended a presentation in 2012 given by a man from GATA (Gold Anti Trust Action Committee, https://www.gata.org, and he said the “real” price should be about five thousand dollars. No doubt that man would say something even higher today.

But there are rumors galore that something really interesting is happening right now. To understand this I need to give a short, oversimplified precis of how the futures markets work.

Let’s say I promise to sell you an ounce of gold for $2000 in July. And you accept that promise. We sign a contract. I don’t even have to have an ounce of gold right now. But I had better have one by the time July rolls around or you take me to court. But I have an alternative! A couple of weeks later, someone else, call him Bob, might post an offer to sell me gold in July, at some price, and I can accept it. Now I don’t need the gold, because Bob will sell it to me just in the nick of time. If that contract was, say, for him to sell me an ounce of gold at $1980, then I just became the man in the middle, taking $2000 from you in July and pocketing $20, and giving Bob $1980. In fact, because all of these are contracts in July, the brokerage house that is keeping track of all these things can make it simple. They can simply give me $20 today, arrange for you to give them $2000 in July and to pay Bob $1980. And they’ll arrange for Bob’s ounce of gold to go to you on delivery day. I’m no longer involved, and never actually touched that ounce of gold, but I made a profit on it.

If gold had gone up instead, I would have lost money. But sometimes when the market goes badly, the best thing to do is take the loss and get out.

Notice that for me to make money, someone else has to lose it. I made $20, but you are going to pay $2000 in July for an ounce of gold that’s only worth $1980.

And if someone manages to manipulate the price the way they like it, someone else just got robbed. Wealth is not created in this kind of market; it’s transferred from a loser to a winner.

That’s basically the futures market. People are buying and selling pork bellies, silver, wheat, eggs, aluminum, or gold at some future date. And the vast majority of them are doing what I was doing…trading the contracts not because I actually care about the product, but just to hopefully make money when the price moves the right way. In fact, because all of the trades happen on a floor, with a broker doing the actual trade, you have no idea you bought your gold from Bob, or who I am. That’s kept track of by the commodity exchange.

In reality gold is traded in contracts for a hundred ounces (on some exchanges) or a kilogram (~32 ounces) on other exchanges. And sometimes there are so many contracts out there that the aggregate total of the contracts is bigger than many countries’ bank vault holdings. But most of this goes up in a puff of smoke about a month before delivery date as people make the opposite contract, cancel out the physical purchases, and pocket their profit (or take their beating). That chain I described from you to me to Bob is likely much shorter than the chains that develop in the futures market.

Some few people do actually buy a gold contract…and actually want the gold.

And this is what has been going on. The value of the contracts is in the mid $1700s per ounce right now. (Even though it’s a 100 ounce contract, the price is quoted per ounce.) Some people, wanting to buy gold and saying $1950 is bullshit when the spot price is about $200 less, are actually going into the futures market, buying a contract at $1750, and saying, “for delivery” which means “Oh and by the way I really do want the gold.”

Over the last couple of years, people have done this perhaps five to ten times as much as usual.

And what do they get? Do they get the gold?

No. At least, not immediately. They get a piece of paper saying that somewhere in a vault in New York or perhaps Delaware, there’s 100 ounces of gold with their name on it. And if they sell the gold via a contract, they are selling the piece of paper.

Which would have its advantages. You don’t have to worry about keeping it in your house and hoping no burglar ever finds it. Or putting it in a safe deposit box and hoping we don’t have a repeat of FDR’s gold heist.

But how do you know that brick of gold actually exists and isn’t the same block of gold some other poor dumb bastard is holding the paper for? In other words, does that piece of paper have a specific piece of gold allocated to it, and no one else?

You can order that vault to actually send you your gold, comma dammit. But they’ll make it painful. It take a lot of work to get this done, and pay who knows how much for shipping. Personally, rather than trust them to ship it to me when I suspect they’d rather pretend to lose it and give me paper money instead, I’d say, “Let me come pick it up.” (For an item worth almost $200,000 I’d make the road trip.) But they probably have rules against that.

There are signs of desperation in the brokerages. People are now being told their contract is good for a 1/4 ownership share in a 400 ounce bar. Which basically makes it impossible for you to actually lay hands on your gold. But at least if they can bring in a bunch of those bars, the paper actually means something.

Apparently last year, over 100 tonnes of gold had to be delivered. I don’t know whether it got physically delivered or people just wanted the receipts, but apparently someone was watching and they had to make sure those receipts were actually covered. Over 100 tonnes. That’s more gold than many major countries have in their central banks’ vaults!

If the commodity exchanges don’t have it in those vaults in Delaware and New York, they have to go get some. Last year about this time, apparently this did happen. They scrambled, but were able to cover it. And no doubt someone had to pay big bucks for gold right now. A lot of people are suspicious that a lot of gold isn’t where it claimed to be, and maybe it’s true. In some cases, a central bank might have leased its gold to someone who then turned around and sold it as jewelry. Meaning the gold is on your earlobes instead of in some vault somewhere, and they won’t be able to get it back. And who knows how many central banks leased their gold to cover this panic?

This sort of thing is apparently continuing to go on. Perhaps that is why you, you little person, you Deplorable proletarian, can’t buy one lousy ounce at the spot price.

If this trend continues, we might actually run out of physical gold; a lot of vaults presumed full will have to be opened and found empty, and futures markets might implode very scandalously. Gold might find its true price, which would make GATA very happy. As well as anyone who has the physical stuff, either in numismatic gold coins or current bullion bars and coins. If you’re holding a piece of paper, on the other hand, then you will be screwed. If you’re lucky some central bank might make “money” out of thin air to pay you for the gold you never actually owned but thought you did.

Or this could be a conspiracy theory in the bad sense of someone just making shit up and marketing it.

But if you think all of this is true, well: Don’t be that person holding a piece of paper. Get actual gold. And suck up the $200 premium over the price of “paper gold” if you have to.

I’ve got some links, some a bit older than others. I am not quite sure what to make of the combined set….are they having trouble now, or not? A lot talks about last year, when they apparently had to scramble to cover over 100 tonnes of deliveries…but they succeeded. Or at least it looks that way. Did someone just hang onto 100 tonnes of paper gold?

Here’s a website that describes the delivery process as it shows that over a hundred tonnes of gold was purchased through the commodities markets about a year ago:

https://www.bullionstar.com/blogs/ronan-manly/the-curious-case-of-comex-gold-deliveries/

Here are a couple of websites talking about this sort of thing–some of them talk of huge deliveries last year but they managed to cover them.

Entities Are Now Having To Take Delivery Of Gold From The Comex As A Last Resort

I can’t quite figure out when this next one was actually written. The charts at the top say yesterday (April 16, 2021). But a lot of the text seems to be suggesting 2017.

https://www.brrcc.org/comex-gold-delivery/

And OMG, here’s SGT report (who ever heard of them?), from back in September.

https://www.sgtreport.com/2020/09/comex-delivery-update/

As one final note, silver is also, similarly, unrealistically priced on the spot (paper) market, an indication that similar things may be happening there. The American Numismatic Association’s magazine, The Numismatist, ran an article this month (or perhaps last month) by one of their frequent contributors asking if there was some way we could derive a real “spot” price for silver that has nothing to do with the paper commodities market. I’m sure he’d say the same thing about gold if asked.

If you invest in precious metals, remember: Physical over Paper. Get your hands on the actual stuff. If you can’t drop it on your foot, don’t bother.

And Joe Biden didn’t win.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·04·10 Joe Biden Didn’t Win Daily Thread

Another week, another deluge of BS from the White House and from the Controlled Opposition. Not much has really happened, so with that noted, on we go.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices

All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend).

Last week:

Gold $1731.80
Silver $25.01
Platinum $1216.00
Palladium $2736.00
Rhodium $26,800.00

This week, 3 PM MT on Friday, markets closed for the weekend

Gold $1745.20
Silver $25.35
Platinum $1205.00
Palladium $2700.00
Rhodium $27,000.00

Gold has tested the $1760 level during the past week, apparently it’s trying to stage a rally.

Palladium

Two more precious metals to go.

This time, it’s palladium.

It, along with rhodium, are the two metals Wollaston discovered closely associated with platinum, shortly into the 19th century. Indeed, since it sits directly above platinum in the periodic table, it’s basically platinum’s little brother.

There’s one unusual property of palladium that attracts a ridiculous amount of attention: It absorbs up to 900 times its volume of hydrogen. It can even be used as a hyrdogen filter if it’s heated: The hydrogen will diffuse through it, other gases mixed in with the hydrogen will not.

People seem to imagine that this would make palladium a great way of storing hydrogen. But consider: It absorbs 900 times its volume of hydrogen, not 900 times its weight, or even half its weight. That’s basically equivalent to putting hydrogen in a very strong tank. But the tank is cheaper (and lighter) than the palladium would be. However, there is one last little quirk about this I’ll get to later.

Palladium, back in the days I first started noticing things, was sort of midway between silver and gold. Silver was perhaps five to ten dollars an ounce. Gold was $300. Palladium was $80.

A few years later, palladium spiked to $900 bucks an ounce…for maybe a year, then dropped back down to very roughly the $200 level. I thought about buying some, thinking it could spike to $900 again, and people basically laughed–it was a very special set of circumstances that had caused that spike.

Well palladium has been doing very well now, pushing towards three thousand dollars an ounce, higher than gold or platinum have ever been, and in fact its price rise preceded the rhodium/iridium madness we’re seeing now.

You can find palladium in solid form; back when it was 80 or 120 bucks I did buy an ounce in the mid 1980s…and it got burglarized away, not very long after that little event I alluded to. It had just shot up to $180/ounce overnight. Back then a precious metal wasn’t listed if you couldn’t buy a pretty little bar of it.

OK, what was the little event? The apparent discovery of cold fusion. In 1989, Pons and Flieschmann claimed that they had gotten hydrogen–deuterium, the stable heavier isotope of it in fact–to fuse at room temperature. How did they do it? They performed electrolysis on heavy water, using a palladium electrode.

Electrolysis is the process where one passes a current through water, and causes the water molecule to split up into its component hydrogen and oxygen atoms. When this is done to heavy water, the hydrogen, of course is actually the deuterium isotope–still hydrogen, but the nucleus contains a neutron as well as the proton, and it’s much easier to get it to undergo nuclear fusion.

So here’s hydrogen being released right next to palladium, right? And palladium is a hydrogen sponge, right? So basically the hydrogen is effectively very compressed, one of the things you’d need to do to it to get it to fuse.

Pons and Fleischmann claimed to have measured more heat being generated than could possibly have come from anything other than fusion, as well as fusion by products. Other scientists, however, failed to replicate their results.

It’s nonetheless an odd thing, because some people claim they do get unusual amounts of heat out of similar apparatuses (apparati?).

My gut feel–and it’s worth exactly what you are paying for it–is that something a little odd is going on here, but that it’s probably not fusion. Some people are still playing with this, but nothing definitive seems to have come out of it. It’s just barely an open question still, in my mind, though I am largely skeptical.

Which is a damn shame, because fusion would solve the energy crisis. It would avert the next ten energy crises. It is what makes the stars shine, and they can shine for billions or even trillions of years. If they were made out of coal that was being burned, instead of hydrogen being fused, they’d only last a few thousand years. Which tells you how very, very, energy dense fusion is.

Other than the usual catalyst uses, palladium is part of the alloy we know as “white gold.” Which must, therefore be more expensive than the regular yellowish-orange gold. Its melting point is actually under three thousand degrees Fahrenheit, no doubt a bit of a change after all of those metals that need to be melted by lightning bolts. It’s a bit lower than platinum’s melting point, and that was managed by the lime block furnace back in the mid 1800s.

Here’s a picture of a credit suisse palladium bar. This was pretty much the first form it came in for investing.

Credit Suisse now makes the PAMP bar, with a bit of artwork on the bar:

The Soviet Union made coins out of palladium back in the 1980s (when it was cheap), and the United States makes a one ounce eagle.

That eagle coin is given a face value of 25 dollars (and is worth a hundred times that!). The obverse is a blown-up version of the “Mercury” (Winged Cap Liberty) dime, while the eagle on the reverse strongly resembles the one on the Walking Liberty half. Instead of his head facing forward, the eagle’s head is bent downwards, grasping what looks like an olive branch.

As you can see the metal is just another silvery-white metal. When not frosty and lustrous it tends to look like stainless steel.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

To conclude: My standard Public Service Announcement. We don’t want to forget this!!!

Remember Hong Kong!!!

If anyone ends up in the cell right next to him, tell him I said “hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·04·03 Joe Biden Didn’t Win Daily Thread

His Fraudulency

One can hope that all is not as it seems.

I’d love to feast on that crow.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices.

Kitco Ask. Last week:

Gold $1734.30
Silver $25.13
Platinum $1192.00
Palladium $2748.00
Rhodium $25,000.00

This week–markets closed 3PM Thursday for Good Friday (or April Fools, depending)

Gold $1731.80
Silver $25.01
Platinum $1216.00
Palladium $2736.00
Rhodium $26,800.00

What I am seeing here is precious metals trading within a pretty well defined range. Gold has dropped down into the 1680s twice but then immediately bounced up. Which implies (to some) that it might be prepping to go up again. Silver seems to be in the doldrums right now; I don’t know whether it’s going up or down (does anyone really ever know about these things?) and won’t even hazard a guess.

Note: Last week’s gold and platinum prices are almost identical to the prices from five weeks ago! Five weeks ago:

Gold $1735.60
Silver $26.80
Platinum $1191.00
Palladium $2379.00
Rhodium $26,000.00

Iridium: The Smoke From The Smoking Gun

4.567 billion years ago, our solar system began to “condense” from the nebula. Clumps of dust particles began to come together, part of a poorly-understood process that eventually led to the planets. The nebula had a potpourri of “stuff” in it. Mostly elements up to iron, with a heavy leavening of ones after iron, created in supernovas or even neutron star collisions. (Most gold is believed to have come out of neutron star collisions…next time you admire that gold coin or your wedding band…think about where that stuff has been! Any of it not from a collision got blasted out of a supernova at 70,000,000 miles per hour.)

Very large bodies, moon sized and larger certainly, would heat up as they formed, from the potential energy of infalling stuff, and also from the fact that this dust had a lot of radioactive stuff in it. Many isotopes with very short half lives, like aluminum 26, were common then; we have no trouble seeing their traces in meteorites today. But back then they were a source of intense heat. Even today, much of the heat of the earth’s interior comes from radioactive decay of uranium, thorium, and even potassium (which has one fairly uncommon radioactive isotope).

Those large bodies became molten, and the heavy stuff sank towards the center. Iron was quite common in the nebula, and iron is heavier than the sorts of things that became typical rocks, and so we today have planets with iron cores.

A lot of good stuff went down into the core with the iron, including gold, the platinum group metals, and silver. Some gold hung around with the lighter slag since gold likes quartz. That resulted in gold being relatively more common than the PGMs in the earth’s crust.

But a lot of things in the solar nebula got big, but not big enough to melt. They became asteroids, and they are relatively rich in PGMs as compared with the earth’s crust. (If we can ever start mining those suckers…PGM prices will go down, and gold will go down somewhat…remember it’s relatively common in the earth’s crust, but that means it won’t become as common, proportionately to where it is today, when we go after asteroids.)

So one sure-fire sign of a meteorite is extra PGMs.

There was once an asteroid the size of Mount Everest. It probably hung out in the asteroid belt for about 4.5 billion years; in fact, it hung out, wherever it hung out, for almost exactly 4.5 billion years.

Then something happened to alter its orbit. And then, sometime after that, perhaps within a million years, it chanced to encounter Earth.

It plunged through the atmosphere–which rapidly raised its surface temperature. Then it slammed into the ocean, at a point just off the coast of what we today know as the Mexican State of Yucatan. The rocks it hit were the worst possible thing it could find…sulfur-rich gypsum, calcium sulfate. The meteorite vaporized in an instant. And so did a lot of that gypsum.

The tsunami in the Gulf probably reached as far inland as Illinois.

The sky was filled with sulfur trioxide, which became sulfuric acid and rained out over the next few days. And the amount of sunlight reaching the surface of the earth was cut, both by the sulfuric crud and just ordinary dust ejected into the stratosphere by the impact, putting another challenge on plant life. Which is at the root of the food chain. Fewer plants, fewer herbivores, fewer herbivores, fewer carnivores.

There’s good reason to believe life was already under stress from massive volcanic eruptions in what is now the Deccan traps, in India. This was just exactly what wasn’t needed for icing on the cake. (Alternatively, the Deccan eruptions may have been triggered by the impact. Yes, even though they were almost on the other side of the world!)

75 percent of species died out, including almost all of the dinosaurs. Some of the ones that had taken to the air and had feathers and warm blood survived the next five years of darkness. And of course many of those little mammals survived too.

Thus ended the Cretaceous Period and the Mesozoic Era (which included the Triassic, Jurassic, and Cretaceous).

The Cretaceous Period had lasted some 80 million years–note, longer than everything since. If you were to go back in time halfway to the beginning of the Cretaceous, you’d be in the Cretaceous.

65.6 million years later, give or take 300,000 years, a couple of geologists were investigating exposed rock near Raton, New Mexico (less than two hours away from me). They knew from fossil evidence that this little thin white stripe in the rock separated Cretaceous from Paleogene (which used to be called the “Tertiary”). Below the line, many kinds of dinosaurs were alive when the rock was deposited. Above it, only the birds.

I’m not 100% positive that this picture is from Raton, but it’s pretty much what it looks like there.

They analyzed the white stripe. It had 100 times as much iridium as the rock above and below it. Still not a lot (a hundred times almost, almost nothing is still almost nothing), but it was the smoke that showed the smoking gun was an asteroid.

An asteroid almost certainly killed the big “Jurassic Park” dinosaurs.

Many have read this story and come away thinking the asteroid was made out of iridium. No, no more than the gun found at the crime scene is made out of fingerprint oil. Iridium was along for the ride, but the sulfur the asteroid found at its destination probably did as much as anything to kill almost every large animal on earth.

So what is this “iridium” anyway? It’s element #77, with 77 protons in the nucleus, tucked in between osmium and platinum. It was discovered alongside osmium in 1803/4 by Smithson Tennant, a story I told last week. It’s almost as dense–the difference is so small you wouldn’t be able to perceive it. And it’s another one of those bothersome high-melting point elements…six hundred kelvins below osmium but still 2400K. But it does not form iridium tetroxide and kill people. In fact, it may be the most chemically inert metal known, the noblest metal. It is not attacked even by aqua regia, a mixture of acids that will make short work of gold.

What I didn’t mention last week was that iridium tended to be the major impurity in those Russian platinum coins. It could be detected while processing the platinum, because at one point during that processing, some of the aqueous solutions would be orange or even red if any iridium were present, rather than yellow. And indeed when analyzed today iridium and iron are the major impurities in those coins.

Today, iridium can be rendered a solid, with some work. This video is well worth watching! Osmium is rarely made into big solid objects. Iridium, on the other hand…

The professor mentioned the price of iridium. It’s now running six thousand dollars an ounce. Back in early December it was $1700, before that it was fairly stable, the ten year chart shows a few years of $1000/oz and even $600/oz iridium, before it blooped up to $1500 in 2018, slowly rose to $1700, and then went bananas. http://www.dailymetalprice.com/metalpricecharts.php?c=ir&u=oz&d=2400

And now for a link to the story of a man who had two kilograms of iridium powder, and decided to go get it melted. Some of you expressed interest in just how it works with these super-high-melting elements; there’s detail here for you.

https://theodoregray.com/PeriodicTable/Stories/077.x3/

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·03·27 Joe Biden Didn’t Win Thread

His Fraudulency

One can hope that all is not as it seems.

I’d love to feast on that crow.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices

Last week:

Gold $1746.90
Silver $26.33
Platinum $1198.00
Palladium $2688.00
Rhodium $29,000.00

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $1734.30
Silver $25.13
Platinum $1192.00
Palladium $2748.00
Rhodium $25,000.00

Gold and platinum are fairly stable, silver took a fairly big hit, Palladium took a healthy jump, and rhodium seems to have dropped 4000 bucks, however, it did so a couple of weeks before and bounced right back up again. I think rhodium has found a range, a wide one…for now.

Osmium. This One Can Kill You.

Someone last week made snarky comments about writing about precious metals, so I figured I’d respond the only way I could: by continuing to do so. In fact, I was thinking about combining osmium and iridium, and now I know I shouldn’t!

Osmium is one of the Platinum Group Metals. In fact, it’s the one directly “below” last week’s metal, ruthenium, in the periodic table.

It’s famous for one thing. It is the densest stable element, bar none. In other words, it’s the most efficient paperweight. It packs more weight into a smaller volume than anything else, bar none…well, at least until you start spooning up pieces of white dwarf or neutron stars. It comes in at 22.59 grams per cubic centimeter–just a shade more than iridium, which we’ll get to in due course.

It also tends to have a slight bluish cast, not unlike zinc (which is neither dense nor valuable). And it’s very hard (Mohs 7.0) and almost completely incompressible.

Provided, of course, that you can get it in bulk. It generally is marketed as a finely-divided powder, and even if you buy melted beads, the beads will often have voids on the inside, because of the same issues that arise when melting any of the refractory metals. That will make the beads lighter than one might expect.

The melting point is a whopping 3306 K, 5491 F, with rhenium and tungsten the only metals with higher melting points. That’s difficult to attain, even in a black car with black interior parked in Phoenix.

Osmium and iridium both were discovered in 1803 as part of the investigation of platinum by Wollaston and Tennant in England. Smithson Tennant gets the credit for osmium and iridium, while Wollaston gets the credit for rhodium and palladium. Tennant found osmium and irididum by studying the black residue left over after dissolving what they thought was pure platinum in aqua regia.

Aqua regia (royal water) is actually a mixture of hydrochloric and nitric acids; unlike other acids, gold will be attacked by aqua regia, and so will platinum. But even after dissolving the platinum, there was this black residue, which (after a lot of trial and error with various chemical reactions) proved to contain two new metals, osmium and iridium.

Osmium proved to have an oxide, OsO₄,. And that’s where the “kill” comes from. Osmium tetroxide is a solid that readily sublimates, turning directly to vapor like dry ice, and it stinks. Hence the name osmium, from osme, “a smell.” Worse: osmium tetroxide is poisonous, and if it doesn’t kill you, it’s liable to damage your eyes.

And if you open a container of powdered osmium, it can catch fire spontaneously, reacting with the air to form osmium tetroxide. This makes it difficult to machine…imagine lathe turnings catching fire and killing or blinding the lathe operator.

Quoting from wikipedia regarding osmium tetroxide:

OsO₄ is highly poisonous. In particular, inhalation at concentrations well below those at which a smell can be perceived can lead to pulmonary edema and subsequent death. Noticeable symptoms can take hours to appear after exposure.
OsO₄ will irreversibly stain the human cornea, which can lead to blindness. The permissible exposure limit for osmium(VIII) oxide (8 hour time-weighted average) is 2 µg/m³.^[7] Osmium(VIII) oxide can penetrate plastics and food packaging, and therefore must be stored in glass under refrigeration.^[14]“
wikipedia

Based on this…you can die from it even if you can’t smell it.

When the Russians made that platinum coinage I talked about a few weeks ago, part of their purification process involved dealing with the osmium they were extracting from the raw platinum in a way that was safe; fairly sophisticated stuff for the early-mid 1800s.

There is good news: even though the powder can kill you, osmium is completely safe (and practically impervious to anything) in bulk form. (It might start to form osmium tetroxide if heated to 400 C.)

Depending on who you ask, osmium is the least common stable element in the earth’s crust…averaging fifty parts per trillion by mass (weight).

Osmium is found with platinum, but also turns up as a by product of copper and nickel mining. Perhaps that is why its price hasn’t gone bananas like some of the other PGMs, whose production depends on platinum mining.

It’s mainly used in alloys, to harden them (rather than as a catalyst). Osmiridium and iridosmine, for instance (you can guess what they are mixtures of). Osmium and its alloys were once used as fountain point pen tips, and still see use as instrument pivots,electrical contacts. Osmium was also used for phonograph needles. Ballpoint pen balls sometimes contain a tiny bit of osmium, too.

Total world production is very hard to nail down, but in 1971 the US produced about 60 Kg as byproduct of copper mining. We import about twice that much, on average, every year. 120 Kg, by the way, is very roughly a gallon and a half of this stuff. (And we are talking about over 250 grocery pounds here. heavy stuff!!) I found in one place a claim that only one or two metric tons is produced per year world wide. (That would be a slab a meter on a side and about four inches thick, tops.)

The “spot” price is hard to nail down on something so thinly traded, but it seems to be about $400 an ounce (and has sat there for years). On the other hand, I’ve also found a site that claims it’s 1200 euros per gram which would make it something like 36000 euros an ounce–probably about 40,000 dollars an ounce. (That flat out doesn’t seem right to me.) If you do find it close to the spot price, it will be in powder form, in a container you had better not break the seal on.

I can’t really recommend it as an investment, the market for it is so small.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

2021·03·20 Joe Biden Didn’t Win Daily Thread

What IS Hopium Anyway?

Based on some of the reactions to my post of two weeks ago, it became apparent that some people misconstrue where I’m coming from.

When I condemn hopium, am I condemning any and all hope? NO. It’s true that hopium is hope, but not all hope is hopium. So when I condemn hopium, I am not condemning hope as such only false and unfounded hope.

In fact, I wasn’t even dumping on all hopium two weeks ago. I was talking specifically of the kind that implies that at some date in the near future, all will suddenly become well, and more specifically, the speculation that names a date. (This is, by the way, something that Q never did, and I am aware of that yet I got criticized on that point as if I were going after Q for naming dates.)

A perfect example, someone posted a thing from John Solomon claiming the long-awaited indictments would be coming out in 4-6 weeks. That means, before the end of April. I have a couple of questions in all earnest to anyone who pays any attention to John Solomon.

How many times has he promised the indictments would be coming in just a few weeks?
How many times has he been right?
Given the answers to 1 and 2, why in blazes is anyone still paying attention to this guy?

Or for that matter to ANY prognostication about a specific date?

I’m thinking we may finally have broken ourselves of that particular habit. Because I don’t see too much of it any more. Good.

And now to clear up a misunderstanding I did my fair share to contribute to.

I had heard others here refer to Marica’s as a place with a lot of hopium, and (my mistake!) I assumed that they meant it included this sort of date-specific stuff. Having misunderstood them, I took them at what I thought was their word. (And I probably shouldn’t have trusted them at all, much less expected them to mean the same thing by hopium as I do.)

So when I said later on that they really needed to get off the hopium, I meant the date specific stuff. And when I went over there later, and picked a random page off that day’s daily…I found no date specific stuff! So I was wrong about that, not that one would necessarily be able to tell, since *I* failed to define my terms. Regardless, it was factually wrong and I apologize.

Not that there isn’t hopium of other types, there, and here.

The emphasis over there is quite a bit different. They’re Deplorable over there, of course, but a lot of the content is about peoples’ personal lives, their other hobbies, their current difficulties, and so on. It may or may not be more your cup of tea than this place (which is 90% politics); if you think you need a change of pace, go have a look-see over there.

OK, one other thing to get out of the way. Someone (either there or here, I do not remember) seemed puzzled that I could say that I believe something is happening, when I clearly don’t believe the “movie set” and “Trump is really in charge” interpretations of today’s events. Am I contradicting myself or backing off from that?

No, because that word something could literally mean a trillion different things, and I don’t believe it means either of the two things I mention above. Trump is doing something, but I doubt it’s a countercoup; more likely he’s doing a bunch of stuff behind the scenes to discredit a lot of bad actors, and trying (quietly) to fix the fraud issues and trying to defeat the worse-than-useless dogpuke RINOs. A lot more mundane than what many are thinking, but it’s all important stuff that has to happen one way or another.

Justice Must Be Done.

The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.

Lawyer Appeasement Section

OK now for the fine print.

This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.

We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.

And remember Wheatie’s Rules:

(Hmm a few extras seem to have crept in.)

Spot Prices

Last week:

Gold $1728.90
Silver $26.03
Platinum $1207.00
Palladium $2426.00
Rhodium $22,000.00

This week, 3PM Mountain Time, markets have closed for the weekend.

Gold $1746.90
Silver $26.33
Platinum $1198.00
Palladium $2688.00
Rhodium $29,000.00

Just when I thought Rhodium might start returning to sane levels…it jumped right back up again. Iridium, too, is going bonkers, in the realm of $5000. It’s a congener of rhodium. (That’s a fancy word meaning “in the same classification group as.” In chemistry, specifically, it means it’s in the same column of the periodic table, which tends to govern chemical properties.)

What’s causing the PGMs other than platinum to go up while platinum is in the dumpster (relatively speaking)? (And the PGMs are: Platinum, palladium, rhodium, iridium, ruthenium and osmium.)

According to one analysis I read, it’s platinum being in the dumpster that is causing all of these problems! (And I can’t verify this, but it makes sense.)

The other PGMs are not mined in their own right; they are quite rare and specifically going after them is uneconomical. Since they do appear with platinum, they are a byproduct of platinum mining. So production of them halts when platinum production halts, and resumes again once someone starts mining platinum.

And platinum was produced a lot back in 2008-2009, to the point where it became a glut on the market. And it is still a glut on the market. Then Covid came along and killed what little platinum production was still going on. The analysts expect this to continue to be a factor until 2024-25.

If they are correct, it’s still a good time to get into PGMs, however, I at least really can’t afford to do so. On the other hand if rhodium, for instance, were to hit $100,000 or more it might just force a restart of platinum mining!

Watch your tailpipes. Your catalytic converter has about $400 in rhodium in it (which as you might imagine, is not much). There is a rash of ~~practitioners of socialist economics~~ thieves sawing off tailpipes on certain model cars now.

Ruthenium

We have five precious metals to go, having done silver, rhodium, platinum, and rhenium already.

Rhenium is very difficult to find in bar form, and so is this week’s metal, ruthenium. (Even rhodium is showing iup in bar form at Kitco, PAMP is making bars now.) Ruthenium is one of the “platinum group metals,” that block of six metals tucked in under iron/cobalt/nickel. If you find a nugget of one of these metals, the others will be in that nugget as impurities.

(It’s important not to confuse the two names even though they’re very similar. Rhenium and ruthenium are different things, even if the only difference in spelling is the “ut.” It’s of the “ut”most importance not to let this confuse you.)

Ruthenium’s density is 12.45, which makes it a bit heavier than lead. But do not use it for bullets; the bad guys are barely worth the regular cost of ammo. And it would probably wreck your rifling, being a lot harder than lead (even jacketed lead). Besides, you’re going to have a very difficult time casting it! It melts at 4,233 F (2607K, 2334 C), which is pretty darned hot–about like the filament in an incandescent bulb (2400K), but other precious metals would shrug even that amount of heat off (e.g, rhenium, which melts at 5767F or 3459K). To give you another notion as to how hot this is, iron melts at 2800 F, 1811K.

Ruthenium was, in fact, the last of the PGMs to be discovered, in 1844, by Karl Ernst Klaus. Don’t let that name fool you. He had German/Baltic ancestry, but he was born in the Russian Empire (and indeed, many Russian scientists had very Germanic names, at the time). He named the element ruthenium, after Ruthenia, the Latin term for Russia.

It appears that Klaus discovered ruthenium while going through the residue left over when refining raw platinum for the Russian platinum ruble coinage that I mentioned a couple of weeks ago. And indeed the timing is right, the series was produced between 1828-1845.

Ruthenium has some catalytic uses (like rhodium, platinum, palladium and iridium), but not to as great an extent, so its spot price seems to be roughly $385-400 depending on exactly where you look. It seems to be slowly climbing. But even so, it’s by far the cheapest of the PGMs…if you can find it in bar form. It usually trades as “sponge” which is to say loose powder.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

Remember Hong Kong!!!

Whoever ends up in the cell next to his, tell him I said “Hi.”

中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!

China is in the White House

Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.

Joe Biden is Asshoe

China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.

But of course the much more important thing to realize:

Joe Biden Didn’t Win

乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!

Justice Must Be Done.

Not an Eagle

Postmodernism, a/k/a “Theory”

Lawyer Appeasement Section

Spot Prices

Electricity and Magnetism (First Half) (Part IV of a Long Series)

Introduction

A couple of go-backs.

Electricity

Conservation of Electric Charge

Magnetism

Electricity Moving. Work and Potential

Digression

Returning to Electricity…

Obligatory PSAs and Reminders

China is Lower than Whale Shit

China is in the White House

Joe Biden is Asshoe

Joe Biden Didn’t Win

Justice Must Be Done.

Lawyer Appeasement Section

Spot Prices

Energy and Potential(Part III of a Long Series)

Introduction

Revisiting Gravity with Vectors.

Energy

Dot Products

Potential Energy

Heat and Chemical Energy

Conservation of Energy

Potential

What makes the stars shine? (Introducing Power)

Obligatory PSAs and Reminders

China is Lower than Whale Shit

China is in the White House

Joe Biden is Asshoe

Joe Biden Didn’t Win

His Fraudulency

Justice Must Be Done.

Lawyer Appeasement Section

Spot Prices.

Update: More info on Valcambi Combo Bars

Velocity and Momentum (Part II of a Long Series)

Introduction

A couple of Go Backs

Velocity

The Vector

Conservation of Velocity?

Nope, No Conservation of Velocity

Momentum

Conservation of Momentum

Rockets and Guns

Vector fun.

Can’t get the drift.

Obligatory PSAs and Reminders

China is Lower than Whale Shit

China is in the White House

Joe Biden is Asshoe

Joe Biden Didn’t Win

His Fraudulency

Physics?

Justice Must Be Done.

Lawyer Appeasement Section

(Paper) Spot Prices

Obligatory PSAs and Reminders

China is Lower than Whale Shit

China is in the White House

Joe Biden is Asshoe

Joe Biden Didn’t Win

Justice Must Be Done.

Lawyer Appeasement Section

Spot (i.e., paper) Prices

Mass (Part I of a Long Series)

Introduction

What Mass Is, and Isn’t

Conservation of Mass

Gravity

Measuring the Solar System, Massing the Earth

Problems with the Law of Gravitation?

Conclusion

Electricity and Magnetism (First Half)
(Part IV of a Long Series)

Energy and Potential
(Part III of a Long Series)

Velocity and Momentum
(Part II of a Long Series)