His Fraudulency
Joe Biteme, properly styled His Fraudulency, continues to infest the White House, and hopium is still being dispensed even as our military appears to have joined the political establishment in knuckling under to the fraud.
All realistic hope lies in the audits, and perhaps the Lindell lawsuit (that will depend on how honestly the system responds to the suit).
One can hope that all is not as it seems.
I’d love to feast on that crow.
Physics?
I anticipate two more “pre 1895” posts after this one. This one is probably the most challenging to date, but you don’t have to be a math whiz to follow it. I don’t do a lot of math in this one, but I certainly describe it, a lot.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Nothing else matters at this point. Talking about trying again in 2022 or 2024 is hopeless otherwise. Which is not to say one must never talk about this, but rather that one must account for this in ones planning; if fixing the fraud is not part of the plan, you have no plan.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
(Paper) Spot Prices
Last week:
Gold $1904.50
Silver $28.03
Platinum $1187.00
Palladium $2878.00
Rhodium $24,400.00
This week, 3PM Mountain Time, markets have closed for the weekend.
Gold $1893
Silver $27.91
Platinum $1172
Palladium $2890
Rhodium $21,000
(Be advised that if you want to go buy some gold, you will have to pay at least $200 over these spot prices. They represent “paper” gold, not “physical” gold, a lump you can hold in your hand. Incidentally, if you do have a lump of some size, doesn’t it give you a nice warm feeling to heft it?)
Very little change to most of these, a slight downward movement (though all except rhodium are up for the day, so we’re seeing prices recovering to previous levels now). Rhodium is getting hit hard, down $3,400 per ounce. Perhaps the bubble is finally bursting.
The Rest of Electricity and Magnetism (Part VI of a Long Series)
Introduction
If you’ve been here a while, you might remember two postings I did on stars. These were independent posts, having nothing to do with politics (poly = many, ticks = blood sucking bugs) and at least some people enjoyed them. I wanted to go to the opposite end of the scale and talk about a certain sub-atomic particle, but then I realized that the best way to do that would be a very, very, very long post. (And yes, it’s a subatomic particle, but it has a lot to do with stars.) A huge part of it would be explaining where physics stood in 1895, and how three discoveries in the next four years basically overturned things, and eventually led to that subatomic particle, the real star (ahem) of the whole series.
So I decided to break this story up into pieces. And this is the sixth of those pieces, and really it’s a continuation of Part IV, which just got to be too long.
And here is the caveat: I will be explaining, at first, what the scientific consensus was in 1895. So much of what I have to say is out of date, and I know it…but going past it would be a spoiler. So I’d appreciate not being “corrected” in the comments when I say things like “mass is conserved.” I know that that isn’t considered true any more, but the point is in 1895 we didn’t know that. I will get there in due time. (On the other hand, if I do misrepresent the state of understanding as it was in 1895, I do want to know it.)
Also, to avoid getting bogged down in Spockian numbers specified to nine decimal places, I’m going to round a lot of things off.
Fields
A lot of what I’ve covered in the past, 4 of the 5 pieces, in fact, have been what physicists call “mechanics” or “kinetics.”
I think we’re finally done with that. Kinetics had to be covered because a lot of its concepts underlie everything else (so you’ll see constant reminders), but I don’t think I need to bring up new kinetics any more (not that there isn’t plenty that hasn’t been covered, including simple harmonic motion, the most likely candidate for a future apologetic go-back).
We are going to pick up on our discussion of electricity and magnetism where we left off, just before Faraday.
(“But these posts are on Saturday,” you say. No, I didn’t say Friday, I said Faraday.)
One important disclaimer here:
Everything I talk about today is assuming our scenarios happen in a perfect vacuum. When not dealing with a perfect vacuum, adjustments must be made which would make things even more complicated than they already are.
So to begin, or actually resume the tale from two weeks ago, let’s back up a bit.
Isaac Newton, when he was formulating the law of universal gravitation, was bothered by something. The way the law works, one mass is affecting another, without touching it. Pretty much everything else one sees, billiard balls, hammers hitting rocks, Antifa beating down regular people, involves some form of direct contact. Action at a distance was odd to him, counter-intuitive. And he was also assuming that gravity was instantaneous. If the sun were to vanish, the earth would immediately begin to move in a straight line, since its primary was now gone, even before the last light from the now-vanished sun reached the earth.
Yet it seemed to be happening, and he could write math to describe it very well. Newton confessed that he couldn’t explain gravity, only describe it.
Now we have electricity and magnetism doing the same thing, and in damn near the same way!
The real answer to this had to wait until the mid 20th century and it’s headache-inducing. But there was an earlier effort in the early nineteenth century, put forward first by Michael Faraday.
Enter field theory, which applies in all three cases. According to this, there is an intangible, massless, motionless “field” for each of these three forces, covering the entire universe, and any mass, electric charge, or magnetic pole basically adds to this field. It’s not action at a distance, because an object out there in the field acts according to the value of the field right where it is, and can be oblivious to what is causing it. Nor does the effect of moving a mass, or charge, or magnet propagate through the field instantaneously: it takes time for the effects of such a thing to be felt on the field.
Nor is this just a semantic change; there will be an actual consequence of the electrical and magnetic fields as such brought up later in this post.
To see how this works, let’s take the simplest one first.
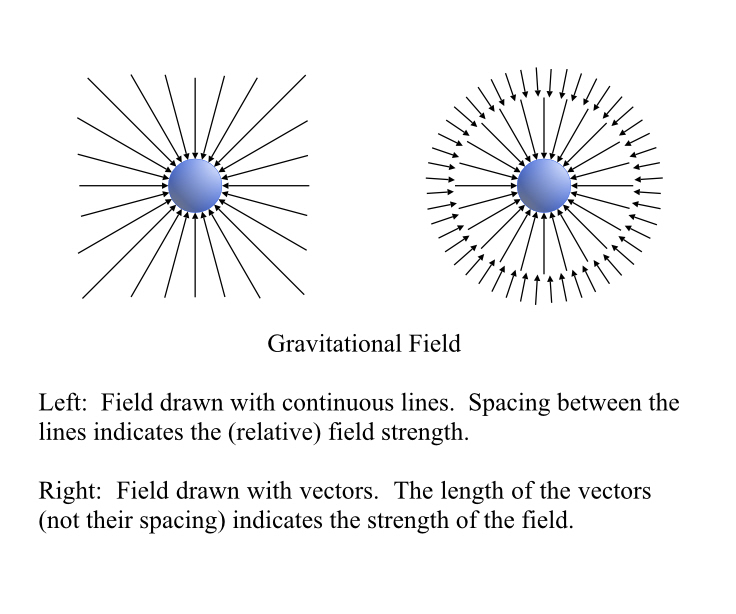
Gravitational Field
Picture some mass, out in the middle of intergalactic space somewhere, quadrillions of miles from anyplace, the corner of “no” and “where.” If that mass were not there, the gravitational field would be very weak or “flat.” But it is there, and its mass causes the gravitational field to “point” toward it. That influence will ultimately extend clear to the edge of the universe, because gravity goes on forever, though in many places it will be overwhelmed by other masses’ effects. This mass’s influence gets weaker and weaker, but never drops to true zero. Sure, at extreme distances it’s a very, very small force, and this contribution to the field would be very tenuous, but it’s still there and as we saw, we can even figure out that if some small body is infinitely far from a large body, we know how fast it will be going when it finally, under the relentless tug of the big body’s gravity, hits it.
(I am, from now on, going to talk as if whatever objects I am considering are alone in the universe. This actually isn’t a bad approximation as long as other things are relatively far away, and it’s a lot easier to get concepts across that way. But someone doing precise measurements in a lab must account for those other things and often they introduce too many external effects for the experiment to be useful.)
There are two ways to picture this field. One is as a bunch of lines radiating out from the object, going off to infinity, with little arrowheads pointing inwards to show the direction of the force. As they get further out, the lines of course get further apart, and there are fewer of them in some given place, and that decrease represents the decrease in strength of the field. In fact it does so perfectly, since the density of lines is going to drop off as the square of the distance, just like the forces of gravity, electricity, and magnetism do. That’s in 3-D; on a 2-D sheet of paper they drop off as the inverse of the distance. That shows there is a geometric basis for the inverse square law.
The actual field strength at any one location is newtons per kilogram. However, the newton already has a kilogram built into it (1N = 1kg•m/s2) so the kilograms cancel and you’re left with a bare acceleration, m/s2.
The other way to pictorially represent a field is to place a little vector arrow at every point in space, making them shorter where the field is weaker.
They’re equivalent, but sometimes one method of visualization is markedly more useful than the other.
Electric Field
Now let’s move on to the next simplest case, electricity.
Every positive charge will, just like gravity, have lines running out of it. Out, this time, because two like charges repel (rather than two masses attracting with gravity). But in the case of electricity, there’s also a negative charge, and lines will run into those charges.
In fact, most of the time, the lines don’t go out to infinity (though they certainly could) but instead end at some negative charge. With gravity, the lines are straight, going out forever, with electricity they will bend towards, and into, a negative charge, and they will be repelled by the lines coming out of some other positive charge. Positive charges are sources, negative charges are sinks.
So even though the electrical force is much, much much stronger than the gravitational one, and it falls off at the same rate (inverse square), electrical forces tend not to be extremely long range. We can certainly see them, but on a cosmic scale they don’t matter nearly as much as gravity, which never gets canceled out.
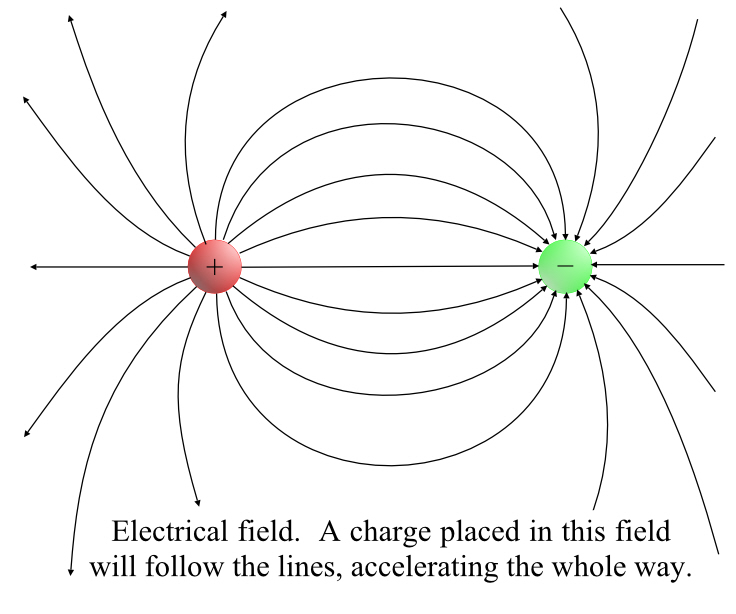
If you let a stationary electric charge go and leave it free to do what it wants, it will follow the field line it’s on, all the way to that line’s end. A negative charge, of course, will go against the arrow, but it will follow the line. If the charge is moving as you turn it loose, it might cross to other field lines depending on which way it’s going when you release it, because the field can’t damp motion perpendicular to the field lines.
There is a special symbol, E, to denote the electrical field. Visually, of course, you can use the diagrams to picture it. Mathematically, it represents the direction and magnitude of the electric force applied by the field. Well, almost. It’s on a per-coulomb basis. A one coulomb charge at a certain point will feel a certain force, a two coulomb charge will feel twice as much force, but the field strength is per coulomb so as to make the field independent of how much it is acting upon. (Of course, the source of the field can have more or less of a charge, but that clearly should change the strength of the field, since it is, after all, the source of the field.) Thus the electric field’s strength is in newtons per coulomb, N/C.
Note that I wrote “direction and magnitude.” Yes, it’s a field of vectors. Every point in space has a specific vector associated with it, and it’s very likely not the same as the vector at some other point just a little ways away.
But we’ve already seen how to represent that. Newton’s law of gravitation and Coulomb’s law give you a vector answer for the force between two objects. Remove one object from the equation and just imagine a measuring device there instead. You get a vector that is the strength of the force. With gravity it’s an induced acceleration on a mass, and that’s analogously true with electricity too, it being an induced force on a charge.
Magnetic Field
Finally, the trickiest one is the magnetic field.
Like electricity, the north pole of a magnet (mathematically represented as positive) is the source of a lot of magnetic field lines, and the south pole of a magnet is a sink for them.
Since there is no such thing as a bare magnetic monopole, with a magnet, even an isolated magnet, all of the magnetic force lines will loop around and hit the south pole of that magnet. And it makes no difference how short the magnet is; every north pole has a south pole of equal strength glued to its backside; actually it might be better to deem the south pole as being the north pole’s backside…and vice versa. Perhaps the best mythic image is that of Janus, the Roman god who had two faces, each on the back of the other. Or perhaps in slightly more modern terms, your average RINO, who is as two-faced as anything in Roman mythology.
Any sort of visible magnet is just a bunch of these magnetic dipoles stacked together, north to south, north to south, with one open-to-the-world north pole at one end and a south pole at the other end.
In fact it’s common to imagine magnetic field lines forming a closed loop, since there’s no distance between the north and south poles of a dipole. Even with two distinct magnets, the field line goes from the first magnet’s north pole, to the second magnet’s south pole, then through that magnet’s body to that magnet’s north pole, then back to the first magnet’s south pole, where it then goes through the first magnet to meet the north pole again, forming, again, a closed loop.
Given that magnets always have a south pole near a north pole, it’s hard to show that the magnetic force is an inverse-square law, because anywhere you measure you’ll be under the influence of both, but it’s true.
The magnetic field is represented by B. Its strength is represented in teslas, yes, named after that Tesla. I’ll hold off on the formal definition of the tesla for a bit since it contains spoilers.
It is with magnets that it’s easiest to actually see the field lines and not just in some cheesy diagram I draw for you. It’s corny but it works: put a magnet under a thin sheet of cardboard, dump some iron filings onto the cardboard, tap it a few times so the filings move, and they will arrange themselves in lines just like these field illustrations.

Gauss’s Laws
We’re now going to take up a bunch of laws concerning electricity and magnetism that were uncovered in the first half of the 1800s. But they all describe the behavior of the fields, not of the charges or poles, so all that stuff up until now has been necessary.
By the very early 1800s, something had become clear about electricity, and that was that the number of field lines that went through any arbitrary surface, was always proportional to the amount of net charge inside that surface. (That’s if you’re using the kind of diagram where the field lines are continuous and the strength is represented by how far apart the lines are. If, on the other hand, you’re using the other kind of diagram…well, I’ll get to that.)
We assume that a line going into the surface is viewed as canceling out a line leaving through the surface.
But that’s almost intuitively obvious with field diagrams. For example picture a positive charge, with some arbitrary surface around it, let’s make it an ellipsoid. All of the lines go through it, outward. See Figure 6-4.
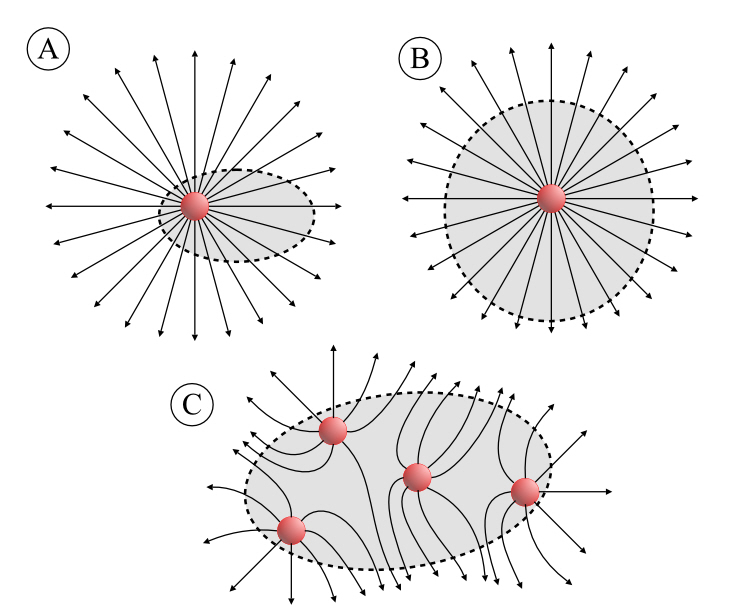
But now draw a second, larger surface (Figure 6-4B). All of the lines go through that, too. The same number of lines go through both spheres, and that number of lines corresponds to the strength of the charge.
But we know the field is weaker, so how does this make sense? Remember that the increasing space between the lines represents the diminishing strength of the field, but the sphere is getting larger. The larger area of the sphere counters the decreasing strength of the field.
Imagine several charges, all positive, inside those spheres. Although the lines will take on an interesting configuration, you’ll see that they all go through both spheres, since they cannot go from one positive charge to another, as in Figure 6-4C.
In fact you can smear the charges out so they all occupy some space, and in fact you can even imagine one large charge spread out over the entire space and the result is the same.
OK, now what happens if there is a small negative charge inside that sphere as well? Some of the field lines from the positive charge(s) will end at the negative charge. If they never cross through our imaginary surface, then clearly there’s no effect. But if they do cross through, then they go back through going back inside to meet their eventual fate in the negative charge. Either way, however many of those lines are collected by the negative charge, they’re subtracted from whatever would go outside and stay outside if there were no negative charge. See figure 6-5.
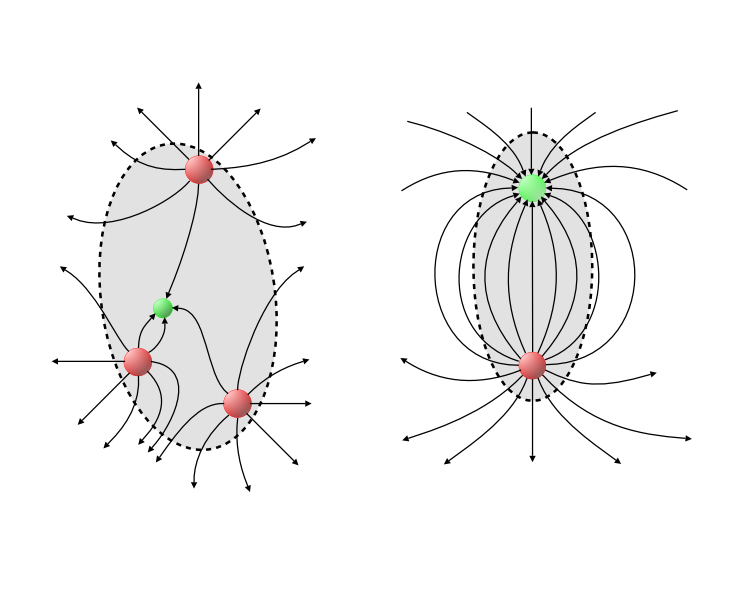
Right, field lines exiting and reentering a surface.
So, basically, if you sum up all of the charges inside the surface, the total number of field lines is proportional to that result.
And this is true for any surface you could draw, anywhere. Even with no charge inside the surface, you could have lines entering from some nearby charge, but they will all leave, net zero.
Of course there’s a weakness to this; because different people are going to draw different numbers of lines for fields of the same strength, or looking at it another way, each person will draw one line for a different amount of charge. So the more mathematically rigorous way is to go over the entire surface and measure the electric field strength at that point, then you have to compensate for cases where the field goes out the surface at a slant. This is for the same reason that an equally bright sun low in the sky won’t heat the ground as that same sun high in the sky–the oblique angle intercepts less sunlight per square meter.
A Whiff of Integration
This is taken care of in the mathematically rigorous form of Gauss’s law for electricity:
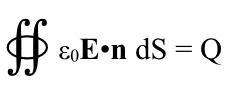
the First Maxwell Equation.
The left side is fancy mathematics speak, it’s actually calculus, but in somewhat-plain English the ∯ and the dS mean, “go over the entire surface, S, bit by bit, and evaluate what’s in between these two pieces at every single point, then add them up.” The two tall s-like things mean a surface, and the oval on top of them means it has to be a closed surface, no openings in it. The E•n just mean to take the dot product of E, and a unit vector perpendicular to the surface at this point. This compensates for any “slant” to the vector (and also turns it negative if it’s diving inside the surface). It’s a convention to label such a unit vector n because “normal to” is another way of saying “perpendicular to” in mathematics. But what is that cute little ε0? It’s our fudge factor. It converts the electric charge into the strength of the field.
Q on the right hand side is the total charge inside the surface. (Sometimes this is written as taking the sum of the charge inside the volume, calculus style, but this is good enough.)
We had a fudge factor k in Coulomb’s equation back in Part IV. Why not use that one here? Because we want to sum up the entire force (per coulomb) over the entire sphere surrounding the charge. The sphere’s area is 4πr2 times its radius, and there’s already an r2 in the denominator of Coulomb’s law, so basically this ε0 is equal to 1/4πk. Or k = 1/4πε0, take your pick.
This new symbol is called the “permittivity of free space” and obviously directly affects the strength of the electric field.
ε0 = 8.8541878128×10-12 C2/Nm2.
This maybe makes more sense if you represent the field with arrows rather than lines, and pick some sort of irregular surface.
This is all advanced calculus and though I’ve tried to explain what it means, I am not going to drag you through an example (even though there are “trivial” ones, like spheres centered on a charge).
OK, that’s Gauss’s law for electric fields (usually just called Gauss’s law). For magnetic fields, there is Gauss’s law for magnetic fields. It’s exactly the same situation, but with magnetic poles inside the surface instead of electric charges, so your mental picture should be almost the same. Here it is:
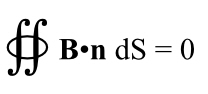
The second Maxwell Equation
Zero!!! We do NOT bother to sum up the magnetic poles inside the surface because we already know there will be an equal number of north and south poles (since they’re literally front and back of the same thing) and the net will be zero! Or you can look at it another way; this law is a positive statement that the sum total will always be zero. There is no way for some spare, bare magnetic monopole to be inside the surface. Any surface, any size, any where.
These two equations are two of Maxwell’s four equations.
Those four equations are one of the most important achievements of mankind’s intellect, ever.
The reason why these are called Maxwell’s equations even though every one of the formulae individually are named for someone else, is that he did the heavy mathematical lifting to bring all the disparate experimental data together to express them into the relatively neat and tidy form you see here.
The two equations I’ve shown are actually one of two forms they can appear in. These are called the “integral forms” and there are equivalent “differential forms.” They’re a lot less intuitive, but much more useful most of the time since they address what’s going on at a single point in space, rather than forcing you to go off and compute or measure things all over some surface or throughout a volume.
Just for completeness, I will present the differential forms, but I’m not going to try to explain them. Ultimately, they mean the same thing as the integral forms, anyway.
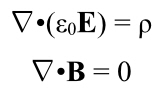
They’re much more compact than the integral forms, and you may have seen me quoting one of these to Wolf in a comment here or there, trying to say “no magnetic monopoles.”
The Connection Between Electricity and Magnetism: Ampere’s Law
The other two of Maxwell’s equations are actually much more interesting for a host of reasons, and in fact modern life would be impossible without them.
But it is going to take a little while to get there.
The next step in our story is the discovery by Hans Christian Oersted in 1820 that an electric current would deflect a compass needle.
So wait a minute. An electric current applying a force to a magnet. Up until now electricity and magnetism had been considered two totally different things. Now, it seems, there is a connection.
In fact, by placing numerous magnets (like compasses) around a wire carrying a current, it can be demonstrated that there is a magnetic field around the wire, in fact it literally runs rings around the wire.

The created magnetic field lines form a closed loop. Even one of these “artificial” magnetic fields that didn’t come from an actual magnet, doesn’t have start and stop points! To a magnet on the field lines, it’s as if there’s a phantom north pole, and a phantom south pole, somewhere else on the ring, but they’re not really there because this field is created by a current, not a magnet.
Here is a drawing of the situation.
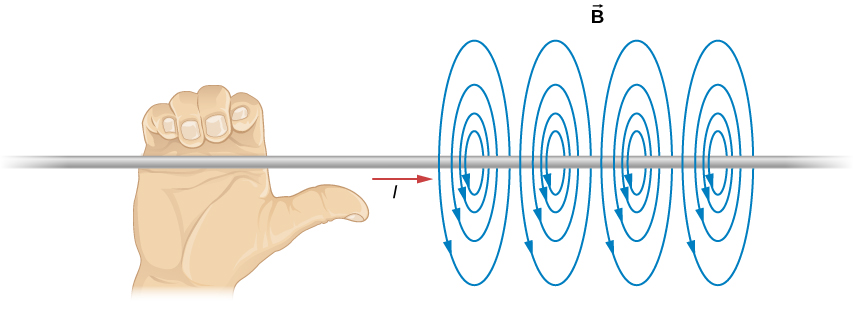
Orient your right thumb in the direction of the current, and your fingers will point in the direction of the magnetic field loops. Yet another right hand rule.
OK, so we now have a closed loop magnetic field line running through empty space. What would happen if we could put a magnetic north pole, by itself, into that field? It would be pushed, repelled by a phantom north pole, around and around and around, speeding up forever, because the line has no end! Of course, there is no such thing as a monopole; a real magnet would basically just swing until the north pole pointed “downstream” towards the phantom south pole of the field and the south pole pointed towards the north phantom pole. They’d both be attracted in their respective directions, but by exactly equal amounts so the magnet would stay motionless.
There is in fact a general law here, Ampere’s law. Draw some kind of closed loop around the wire. Stretch a surface across that loop–it doesn’t have to be flat, any shape of surface will do. Note that this time it’s not a closed surface, far from it! This surface is how the mathematicians “capture” the current through the wire, because in reality, it could be going through several wires, or it could be a bolt of lighting with no wire at all! The net current going through the surface is what counts.
If you walk around that loop, the net magnetic force going around that loop is directly proportional to the amount of current going through the surface.
Here’s the equation.
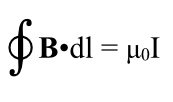
part of Maxwell’s 4th Equation
Now on the left we are adding up around a loop, in other words following a line, l, which is one dimensional so only one ∫. It’s a closed loop, hence the circle. We again dot B with the line of the loop; we get to add more to that total if we are walking along B than if we’re walking at some slant to it.
We again see ourselves multiplying by a fudge factor, this is a new one, μ0.
This one is called the permeability of free space (not to be confused with the permittivity of free space, above). Its value is:
μ0 = 4 π x 10-7 N/A2.
Note that it’s defined in terms of amperes!
This law, by the way, is a case where the strength drops off, not as 1/r2 as you get further away from the wire, but as 1/r. But this makes some sense if you think about it. If you walk in a perfect circle one meter from the wire, you’ll cover a certain distance (2π meters) and total up some certain amount of magnetic field times length. Walk further away, 2 meters, and you’ve now walked a total of 4π meters, but according to this law, you’ve encountered the same total. But the only way that can be is if B is half as strong, not a quarter as strong.
This law, including the concentric rings of the magnetic field, can be demoed with the same iron filing trick as was used with the bar magnet. Just remember that the wire has to be perpendicular to the plane of the cardboard the iron filings are on (best to make it vertical so the cardboard lies flat.
This law is what allows one to create an electromagnet, most effectively with a coil of wire. If you draw a closed loop through the center of the coil, and then around the outside of the coil, every single turn in that coil runs through the closed loop in the same direction, and the current each time can add up (even though it’s the same current “circling back”).
Electromagnets are the heart of many electric motors, and many loudspeakers. So this law is of very great importance in our modern lives.
But this is only part of this law. Ampere didn’t recognize the other factor involved. I’ll get to it in due course. So what I’ve shown is only part of the fourth Maxwell equation.
Faraday’s Law
Yes, I skipped over number 3, because I’m saving the best for last! (Of course, I didn’t really skip over it because I didn’t actually present the fourth equation, did I?)
Now we get to the really important one. It’s so important, it’s one of the most important facts out there.
Up until Faraday’s work, there were only two ways to generate electricity as a current so it could do some work. One was to arrange to continuously produce static electricity and draw it off as it was being created. The other was to build a battery. But when the battery ran down, there was no way to recharge it, other than to take it apart, replace the wet cardboard and build it again.
The fact that an electric current–a flow of the electric fluid–could create a magnetic field made just about everyone involved wonder if there was a way to create an electric current using a magnet.
Early experiments were disappointing. Simply setting a magnet near a wire, or even a coil of wire, did nothing. Michael Faraday, however, in the early 1830s discovered that a moving magnet would cause an electric current in a nearby wire, and the effect was stronger moving the magnet into and out of a coil of wire. The key was the change in the magnetic field (getting stronger as the magnet approached the wire, or getting weaker as it moved away), more than it was the mere fact of the magnet moving. This is known as Faraday’s Law. The current would flow in one direction while the magnetic field was getting stronger, then flow in the other direction when it got weaker.
Upon this discovery, modern life is utterly dependent.
Any electrical generator uses this fact, from your backup generator to hydroelectric dams to coal fired plants to nuclear power. And yes, even the bird-killer wind turbines. All generate electricity via this principle. If we did not have this, everything electrical or electronic would depend on batteries, which might not sound so bad until you realize there would be no way to recharge the battery.
The only exception to this is solar electric power (i.e., photovoltaics), and that is a much newer innovation, so imagine where we would have been without the generator!
We owe Faraday a YUUUUGE debt. Thank him the next time you flip a light switch. Or hit any power button on anything.
Well, this led to Faraday’s law, which got bundled up with Maxwell’s Equations as the third such equation.
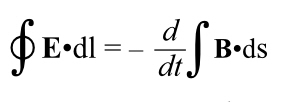
Maxwell’s Third Equation.
That right hand side looks a bit odd, because it has a d/dt in it. We’re used to summing things up over surfaces (closed and partial), and around closed loops, but this is a new wrinkle. But it’s not bad, conceptually. Basically, the d/dt means “the rate of change of” what follows it. And what follows it is the magnetic field going through the surface enclosed by a loop. So: as the magnetic field changes, it creates an electric field, if it changes fast it creates a stronger electric field. If that electric field is near a wire, it will make a current flow. Voila! Now there is a negative sign, so basically, a positive change in the magnetic field will produce a negative current through the wire, by the time you figure out all the directions involved.
That’s the third of Maxwell’s equations.
Maxwell’s Fourth Equation, Completed
Now let’s pick up where we left off with the fourth one.
It turns out that when dealing with the magnetic current around a current, there is also a term for a changing electrical field.
Now any small electrical field associated with the current isn’t going to matter, if the current is constant, it’s because the electric fluid in the wire is being driven by a constant electric field.
But if the electric field through that surface changes, then we get an additional contribution to the magnetic field, in a mirror image of the way changing magnetic field inducing an electric field (and causing a current).
So here is the fourth of Maxwell’s equations, in full.
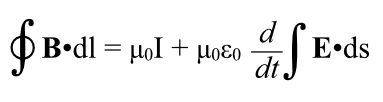
the Fourth Maxwell Equation
Nothing new here; if you can get the gist of the others through my attempts to explain them you should have this one knocked.
The third and fourth of Maxwell’s Equations also have their differential forms, which I am going to present without explanation.
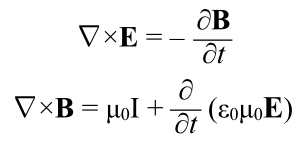
We now have four equations that completely describe the behavior of electricity and magnetism.
In fact it should be plain by now that electricity and magnetism are joined at the hip. We should, in fact, be speaking of “electromagnetism” not “electricity and magnetism.”
Work can be done to describe them with alternating fields, i.e., where the fields flip back and forth. In fact if this is done it’s possible to set up a situation where the E and B fields propagate each other across space, since each can be generated by a change in the other. But hold that thought.
James Clerk Maxwell
(Clerk is pronounced British-style, as “clark.”)
You might have noticed that every single one of the four of Maxwell’s equations is named after someone else, Gauss, Ampere, or Faraday. Does this make him a Joe Biden-level plagiarist? (Remember in 1988 when Biden’s campaign for the Democrat nomination was sunk because he turned out to be a plagiarist? It’s now much more difficult to sink a Democrat, isn’t it?)
No, it doesn’t. Because Maxwell (1831-1879, a disappointingly short life) was the person who did the math that tied these laws together. In particular, Faraday could do his experiments and could verbally describe what he had seen, but he had no formal mathematics background to speak of. He would never have understood his own law, in the form I wrote it above.
Not that it was easy, even for Maxwell; he published his big work tying everything together mathematically in 1865. At the time, this was second only to Newton as a grand unification of a bunch of different physical phenomena. I was not kidding when I said Maxwell’s Equations were one of the most important achievements of human intellect, ever. Imagine your life without electricity, ever (and not just for a power outage), and you will see the practical importance of these laws even if you can’t (yet) visualize their mathematical elegance.
Magnetic Deflection of an Electric Charge
There’s another connection between electricity and magnetism I want to bring up.
What happens to an electric charge in a magnetic field?
Well, nothing. Magnets respond to magnetic fields, electric charges respond to electric fields.
Ah, but what if the electric charge is moving? (It does seem as if something has to be moving, or at least changing, for the connection between electricity and magnetism to manifest.)
In that case a force is generated by the magnetic field. But that depends on the direction of the motion of the charge and the direction of the magnetic field.
In fact, here’s our cross product again!
F = qv × B
If a particle is moving up, and the magnetic field points into the computer screen, the force pulls the particle to the left. After a split second of this, the particle is now moving slightly to the left of upward, and the force is left and a little bit downwards. After a bit of that the particle has turned some more. In fact it will start to go around and around in circles.
It won’t do this forever, it will lose velocity to various effects I’m not going to get into (even if it’s not meeting any air resistance). But if you can figure out how to pump energy into the particle you can keep it going round and round for as long as you do that. An electric field can be used to pump the particle up, just be sure to switch it off just as the particle passes it so the field doesn’t put the brakes on the particle. (This is how cyclotrons work; why you need a cyclotron, however, is post 1895. This is also how mass spectrometers work, but again…post 1895.)
I didn’t define the tesla, the unit of magnetic field strength, before. And that’s because it relies on this fact, which wasn’t actually formulated until well after Maxwell put forward his equations; it’s a part of the Lorentz equation.
A one tesla field is one where a charge of one coulomb, moving at one meter per second experiences a force of one newton. Or, it generates one newton per coulomb, per meter per second. Thus:
1 T = 1N/(C•m/s) = 1N•s/(C•m).
If you look at that you have s/C, which is the same as 1/A. So most usually,
1 T = 1 N/A•m
Note that the magnetic field strength is defined based on electrical stuff using the electrical current unit.
A lot of these physical laws have “fudge factors” in them. Many of the others really also have fudge factors too, but the units are defined in such a way as to cause those fudge factors to be 1. The fudge factors depend on our choice of units. For example, remember that:
ε0 = 8.8541878128×10-12 C2/Nm2.
Part of the definition of this is the coulomb, squared. What if a coulomb were half as big as it actually is? Then we’d have to multiply the number by four to make up for it!
If we had defined a tesla independently of the ampere, there would be a fudge factor involved getting from there to amperes, and the μ0 fudge factor would be different too.
But we defined the tesla based on the ampere, so the fudge factor μ0 is based on the ampere. Of course the ε0 fudge factor was also based on the ampere.
So any relationship between or involving these two numbers is probably not a coincidence, because they’re both based on the same thing.
Let There Be Light
Look again at Maxwell’s fourth law. There’s a μ0ε0 in it. We have to multiply the two together to apply that law (in either form).
Well, let’s do that. Let’s multiply them together!
The value of ε0 is: 8.8541878128x 10-12 C2/Nm2
The value of μ0 is: 4π x 10-7 N/A2
So, combining the two actual numbers (well, just their exponents), we have:
ε0μ0 = 4π•8.8541878128 x 10-19 NC2/A2Nm2
The newtons cancel.
ε0μ0 = 4π•8.8541878128 x 10-19 C2/A2m2
Amperes are simply coulombs per second, or to put it another way, coulombs are amp-seconds. So replace C2 and A2s2 and then cancel the amperes.
ε0μ0 = 4π•8.8541878128 x 10-19 A2s2/A2m2
ε0μ0 = 4π•8.8541878128 x 10-19 s2/m2
Now we finally have to do the arithmetic.
ε0μ0 = 1.11265005544 x 10-17 s2/m2
Let’s take the square root of that. s2/m2 will become s/m.
sqrt(ε0μ0) = 3.3356440951 x 10-9 s/m
That looks like it’s the inverse of a velocity. Seconds per meter instead of meters per second. So divide into 1, and get:
1/sqrt(ε0μ0) = 299,792,458 m/s.
That should be familiar to a great many of you as…the speed of light. (Which is presently, by definition, exactly this number of meters per second. The meter, in fact is defined in terms of the speed of light. Why this makes sense…is a topic for a future post.)
So basically,
ε0μ0 = 1/c2
where c is customarily the speed of light.
But, what the heck is the speed of light doing showing up in Maxwell’s equations?
Remember when I said that under the right circumstances, a varying electrical field could produce a varying magnetic field, which could produce a varying electric field, and they could propagate through space? It takes a lot of math that I won’t dive into here to show it, but if you can arrange for an electric field to oscillate in a sine wave (so that E is proportional to the sine of the time), you will get a companion magnetic field doing the same thing, and they will propagate in a direction perpendicular to both fields.
And they will propagate at the speed of light.
And light is what you get when this happens.
Maxwell’s equations turn out not just to be about electric current and magnets, they turn out to be about light.
Who’da thunk?
And this is why I said, early in this post, that fields are not just a semantic thing. You cannot get from action-at-a-distance Newtonian style physics to light as an electromagnetic wave, but you can if you start with fields.
In fact, I’m going to share with you a bit of geek humor. It goes:
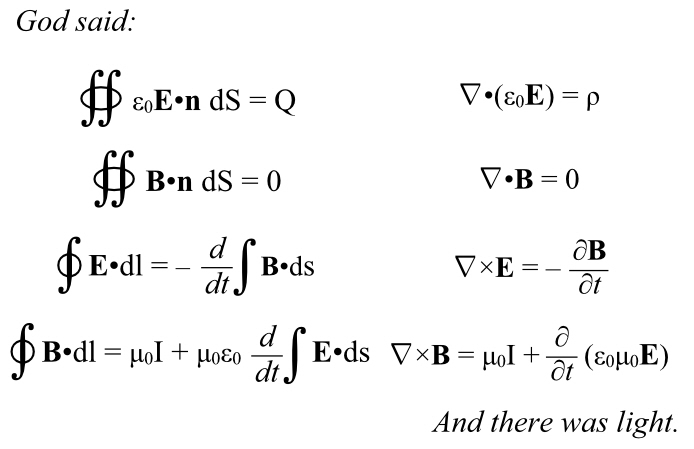
Conclusion
As we continue this series, it’s going to turn out that as far as anyone in 1895 could tell, the combined “electromagnetic force” underlies every physical phenomenon in our daily lives, other than gravity, which we already understood.
I wasn’t kidding about Maxwell’s Equations.
(There was one very big fact that they took for granted that isn’t due to electromagnetism nor gravity. Something they probably hadn’t bothered to ask.)
So, to someone in 1895, it really was starting to look like we had reality knocked. Yeah, there were a few mysteries out there, but we’d figure them out or reconcile them.
The last time we talked about electricity and magnetism, I brought up a conservation law, the conservation of electric charge. Since this is really a two-piece part to this whole thing, I mentioned that there was also a mystery which I would defer until now. So here it is, our 1895 mystery.
I’ve talked about electrical fluid. But what, exactly, is it? And really, do we know whether Franklin or DuFey was right about it? Are there two fluids, or one?
As 1895 dawned, we had one tantalizing clue, and a bunch of other info that would turn out to be important in answering the question.
And that came from the study of atoms.
Obligatory PSAs and Reminders
China is Lower than Whale Shit
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!
