A Caution
Just remember…we might replace the RINO candidates. (Or we might not. The record is mixed even though there is more MAGA than there used to be.) But that will make no difference in the long run if the party officials, basically the Rhonna McDaniels (or however that’s spelled–I suspect it’s RINO), don’t get replaced.
State party chairs, vice chairs, secretaries and so on, and the same at county levels, have huge influence on who ultimately gets nominated, and if these party wheelhorses are RINOs, they will work tirelessly to put their own pukey people on the ballot. In fact I’d not be surprised if some of our “MAGA” candidates are in fact, RINO plants, encouraged to run by the RINO party leadership when they realized that Lyn Cheney (and her ilk) were hopelessly compromised as effective candidates. The best way for them to deal with the opposition, of course, is to run it themselves.
Running good candidates is only HALF of the battle!
SPECIAL SECTION: Message For Our “Friends” In The Middle Kingdom
I normally save this for near the end, but…basically…up your shit-kicking barbarian asses. Yes, barbarian! It took a bunch of sailors in Western Asia to invent a real alphabet instead of badly drawn cartoons to write with. So much for your “civilization.”
Yeah, the WORLD noticed you had to borrow the Latin alphabet to make Pinyin. Like with every other idea you had to steal from us “Foreign Devils” since you rammed your heads up your asses five centuries ago, you sure managed to bastardize it badly in the process.
Have you stopped eating bats yet? Are you shit-kickers still sleeping with farm animals?
Or maybe even just had the slightest inkling of treating lives as something you don’t just casually dispose of?
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
And here’s my response to barbarian “asshoes” like you:
OK, with that rant out of my system…
Biden Gives Us Too Much Credit
…we can move on to the next one.
Apparently Biden (or his puppeteer) has decided we’re to blame for all of the fail in the United States today.
Sorry to disappoint you Joe (or whoever), but you managed to do that all on your own; not only that, you wouldn’t let us NOT give you the chance because you insisted on cheating your way into power.
Yep, you-all are incompetent, and so proud of it you expect our applause for your sincerity. Fuck that!!
It wouldn’t be so bad, but you insist that everyone else have to share in your misery. Nope, can’t have anyone get out from under it. Somehow your grand vision only works if every single other person on earth is forced to go along. So much as ONE PERSON not going along is enough to make it all fail, apparently.
In engineering school we’re taught that a design that has seven to eight billion single points of failure…sucks.
Actually, we weren’t taught that. Because it would never have occurred to the professors to use such a ridiculous example.
Justice Must Be Done.
The prior election must be acknowledged as fraudulent, and steps must be taken to prosecute the fraudsters and restore integrity to the system.
Lawyer Appeasement Section
OK now for the fine print.
This is the WQTH Daily Thread. You know the drill. There’s no Poltical correctness, but civility is a requirement. There are Important Guidelines, here, with an addendum on 20191110.
We have a new board – called The U Tree – where people can take each other to the woodshed without fear of censorship or moderation.
And remember Wheatie’s Rules:
1. No food fights
2. No running with scissors.
3. If you bring snacks, bring enough for everyone.
4. Zeroth rule of gun safety: Don’t let the government get your guns.
5. Rule one of gun safety: The gun is always loaded.
5a. If you actually want the gun to be loaded, like because you’re checking out a bump in the night, then it’s empty.
6. Rule two of gun safety: Never point the gun at anything you’re not willing to destroy.
7. Rule three: Keep your finger off the trigger until ready to fire.
8. Rule the fourth: Be sure of your target and what is behind it.
(Hmm a few extras seem to have crept in.)
Spot Prices
All prices are Kitco Ask, 3PM MT Friday (at that time the markets close for the weekend).
Last Week:
Gold $1,914.10
Silver $22.75
Platinum $921.00
Palladium $1,338.00
Rhodium $4,750.00
So here it is, Friday, 3PM MT after markets closed and we see:
Gold $1,890.50
Silver $22.86
Platinum $923.00
Palladium $1,288.00
Rhodium $4,550.00
Gold sliding. I guess to Wall Street things are just fine. Meanwhile we work for bullshit pay and inflation keeps on going…
Watch Me Pull A Rabbit Out Of My Hat

Last week we left off showing that it’s possible using the Maclaurin series (a special case of the Taylor series) to compute sines and cosines of angles. The closer the angle is to zero, the easier it is to do.
Technically you don’t get an exact answer unless you run the series out forever, but you can typically get acceptable precision in just a few terms.
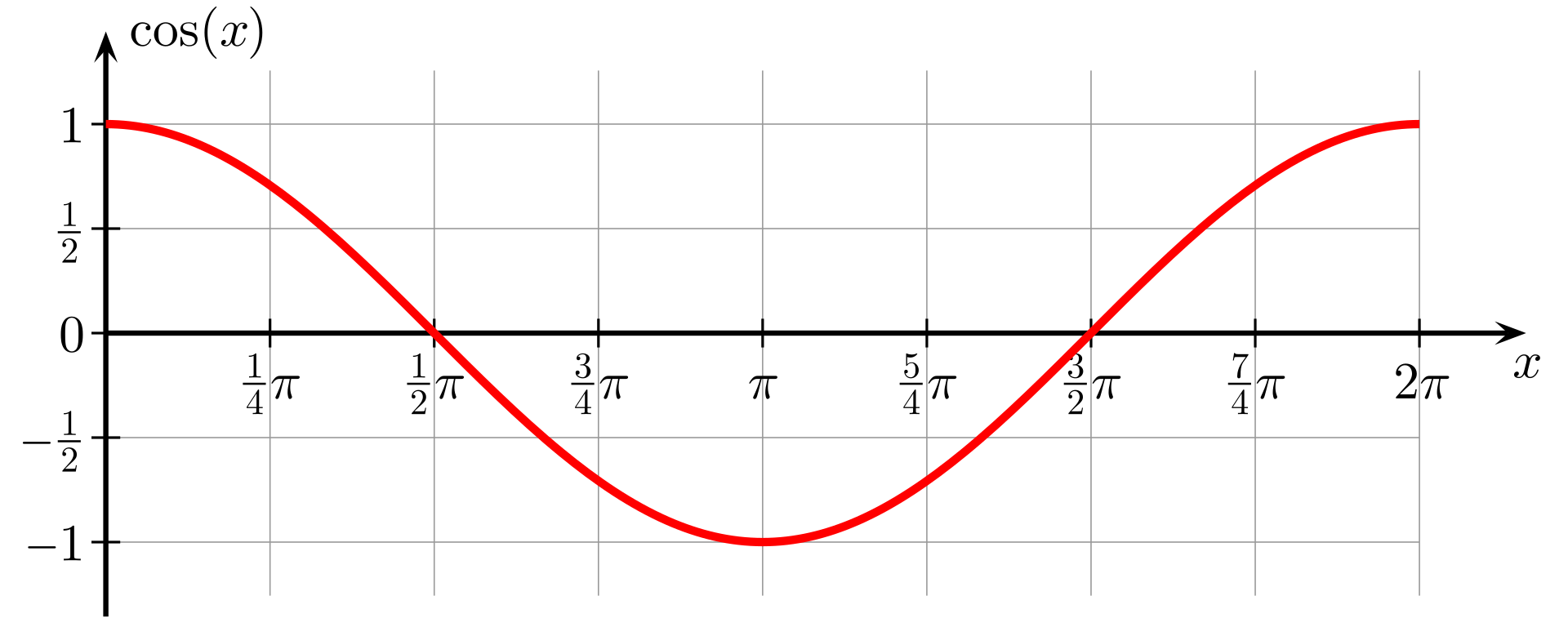
Here they are, sine and cosine:
sinx = x – x3/3! +x5/5! – x7/7!…
cosx = 1 + –x2/2! + x4/4! + –x6/6! + x8/8! +…
But if you recall, from way back, there is another such series for the exponential function, i.e., ex.

(It’s so much nicer when I can find an image of a properly typeset formula, ain’t it?)
Can We Tie Trig and Exponentials To Each Other?
Take a really close look at these three formulas. Compare like terms…and by that I mean x3 in one formula should be compared to x3 in another, and so on.
You’ll notice that the formula for ex contains terms for every power of x. Sinx, on the other hand contains only the odd-power elements, and cosx contains only the even-power elements.
It’s almost as if you could somehow combine sine and cosine to get the exponential function.
But if you add the sine and cosine functions together you get this:
sinx + cosx = 1 + x – x2/2! – x3/3! + x4/4! +x5/5! – x6/6! – x7/7! + x8/8! +…
Well…it’s almost right. Except for one rather awkward problem. The terms have two positive signs, then two negative signs, then two positive signs, then two negative signs. and so on, whereas the exponential series has nothing but positive signs.
And you can’t fix this by subtracting cosine from sine (or vice versa), thereby flipping some signs, because some of those errant negative signs come from sinx and some from cosx.
For example:
sinx – cosx = -1 + x + x2/2! – x3/3! – x4/4! +x5/5! + x6/6! – x7/7! – x8/8! +…
You still have an alternating sequence of two positive numbers then two negative numbers, then two positive numbers, and so on; you’ve just shifted where the pairs of negatives and positives are in the sequence.
So what looked like something that would have been a really cool way to tie trigonometry to the exponential function, fails.
Tying Up A Loose End
I mentioned here: https://www.theqtree.com/2023/06/24/2023%c2%b706%c2%b724-joe-biden-didnt-win-daily-thread/ that complex numbers, i.e., numbers of the form a + bi, where i is the square root of -1, could have all sorts of things done to them, addition, subtraction, multiplication, division…and you could even raise other numbers to complex powers. I said that last part, but then I said I’d have to talk about it some other week.
Well, this is that week.
Nothing says that the x in the Maclaurin series has to be a real number.
So why don’t we plug a complex number into the Maclaurin series for ex to see what happens?
Well I can tell you beforehand what will happen if we plug a + bi into it…we’re going to have to square that expression, then cube it, then raise it to the fourth power, and the fifth, and we will have a gawdawful mess on our hands very, very quickly.
But really, that would be a chimpanzee move.
ea+bi, after all is ea x ebi. By splitting it up this way, we can handle the two pieces separately and then (at the end) multiply them together. We already have a handle on ea but we should check on ebi since the power we are raising e to is an imaginary number. So let’s set ea aside (but we will not forget it’s there).
Using the ex Maclaurin series:

…and setting x = bi, we get:
ebi = (bi)0/0! + (bi)1/1! + (bi)2/2! + (bi)3/3! + (bi)4/4! + (bi)5/5! + (bi)6/6! + …
This doesn’t seem to do much for us; you could put anything in for x and you will be raising it to all those powers. But i has a very interesting behavior when you raise it to successive powers, and we can use that here:
i0 = 1, i1 = i, i2 = -1, i3 = –i, i4 = 1, i5 = i, i6 = -1 i7 = –i ….
In other words it goes through a 1, i, -1, –i cycle, over and over again. So we can go back to the expansion above and replace all of the i-to-the-somethingth powers with the appropriate value (and do more simplifications….0! is defined to be 1, and any number raised to the 0th power is also 1). Also, when we do this if there is an i or –i we’ll bring it to the front.
ebi = 1 + ib – b2/2! – ib3/3! + b4/4! + ib5/5! – b6/6! – ib7/7! …
Now some of the terms have i in them and some do not, which makes this the epitome of a complex number. It’s a little hard to deal with this in this form, so let’s collect all the real terms together, and all the imaginary terms together–like we would for any complex number. We end up with the sum of two series:
ebi = 1 – b2/2! + b4/4! – b6/6! + … (first series)
+ ib – ib3/3! + ib5/5! – ib7/7! + … (second series)
And we can factor out the i from the second series:
ebi = 1 – b2/2! + b4/4! – b6/6! + … (first series)
+ i (b – b3/3! + b5/5! – b7/7! + …) (second series)
Does anything look familiar?
I ask again, DOES ANYTHING LOOK FAMILIAR?!?
It better.
The first series is the same as the expansion of cosx from earlier, except of course it’s on b instead of x. Makes no difference. They’re the same.
The second series, moreover is i times the sinx series from above (again with b substituted for x).
In other words, switching back to x:
eix = cosx + isinx.
Well, well, well. We can connect exponentials and trig functions after all! We just needed a bit of (I can’t resist) imagination, taking the exponent of an imaginary number and getting a result that has both a real and imaginary component.
This is known as Euler’s equation, after Leonhard Euler (1707-1783) who first noted it. Euler is arguably the greatest mathematician that ever lived though he has plenty of stiff competition from others.
It would be hard to overstate the importance of this result. It underlies much of physics, and is all over the place in electrical engineering.
And yet you never hear about it in the popularizations of science (well, not until now).
This is largely because, in order to get here, you need a pretty solid advanced math background. Or someone who’s willing to skip over a lot of formal proofs as he presents it to you. Most math educators won’t do that, and rightly so. Mathematics education relies on proving everything along every step of the way. It’s bullshit-free, everything is proved based on what comes before and you don’t have to trust the perfessor or take his word for anything. And here I am giving it to with little in the way of proofs and enough hand-waving that I am raising myself off the floor from flapping my arms so hard. (As such, if you find this interesting, I ask that you at least ask someone else with the right knowledge if it’s true. DO NOT just take my word for it. Better yet, take a bunch of math courses.)
Putting It Back Together
But there’s one little detail that must be dealt with. We got here by trying to raise e to the a+bi power, and we set aside the ea that we must multiply ebi by. So let’s put them back together.
ea+bi = eaebi = ea(cosb + isinb)
But now, the last thing should remind you of something. (Though this time I will not jump on the table and yell that it should do so.)
It looks a bit like how you convert polar to rectangular coordinates.
<r, θ> = (rcosθ , rsinθ)
And if you consider your rectangular coordinates to be complex number in a complex number plane, you get:
<r, θ> = r(cosθ + isinθ)
So another way to represent ea+bi is:
ea+bi = <ea, b>
I’ve said before that the angle brackets < and > are not standard mathematical notation. I just use them as a visual cue that the coordinates are polar coordinates. Mathematicians generally don’t bother with that, they just use parentheses for both cases. But sometimes (actually rather often) they will write polar coordinates like this:
<r, θ> as: reiθ
(And need I remind you: the angle must be expressed in radians. eiθ will give you the sine and cosine of θ, but only if θ is radians. Another reason why mathematicians prefer radians.)
A Maximally Geeky Bonus
What if θ is π? (I.e., what if θ is 180 degrees?)
The sine of π is zero. The cosine of π is -1.
So if eiθ = cosθ + isinθ, and θ = π, then eiπ = cosπ + isinπ = -1 + 0.
eiπ = -1
Adding 1 to both sides we get:
eiπ + 1 = 0
Note the beauty of this. It contains all three of the numbers I introduced you to, e, π, and i, plus the numbers 0 and 1–which I sure hope I did not have to introduce you to (though maybe some reader of this took woke mathematics and got to hear about “saving the planet” instead of actual math).
Arguably these are the five most important numbers in mathematics, and one formula ties them together, and no other more mundane number appears in the formula.
This is known as Euler’s identity, and it’s a favorite. There’s absolutely no way anyone can see this intuitively, no way to see that e, i, and π should be related to each other in any way, much less all three of them directly like this.
And yet they are. And much of our modern world depends on this crazy little fact.
Obligatory PSAs and Reminders
China is Lower than Whale Shit
Remember Hong Kong!!!
中国是个混蛋 !!!
Zhōngguò shì gè hùndàn !!!
China is asshoe !!!
China is in the White House
Since Wednesday, January 20 at Noon EST, the bought-and-paid for His Fraudulency Joseph Biden has been in the White House. It’s as good as having China in the Oval Office.
Joe Biden is Asshoe
China is in the White House, because Joe Biden is in the White House, and Joe Biden is identically equal to China. China is Asshoe. Therefore, Joe Biden is Asshoe.
But of course the much more important thing to realize:
Joe Biden Didn’t Win
乔*拜登没赢 !!!
Qiáo Bài dēng méi yíng !!!
Joe Biden didn’t win !!!











































:max_bytes(150000):strip_icc():format(webp)/_equity_final-a71099b17173432f813b15202e64459d.png)